Спрос, с точки зрения количества, – определенная величина стоимости товара, находящегося в относительной форме. Величина спроса, с точки зрения количества, – количество товара-эквивалента, или количество потребительной стоимости товара-эквивалента, ПСA .
2. Комбинации простой формы стоимости. Законы количественной определенности простой формы стоимости
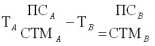
вдвойне сложна для количественно-математического анализа, поскольку каждая из двух ее частей описывается рассмотренными выше многочисленными комбинациями двух факторов товара.
Рассмотрим две простейшие комбинации:
1) ПРA и ПРB, СЕТA и СЕТB,– неизменны,
2) ПРA и ПРB, СЕТA и СЕТB меняются.
Первая комбинация простой формы стоимости: неизменная производительная сила общественного труда A и B
Если в уравнениях базового и текущего периода
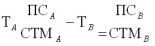
производительная сила общественного труда и, соответственно, стоимость единиц товаров остается неизменной, то относительная стоимость (цена) единицы товара неизменна.
К этому выводу можно придти, если взять полную формулу цены:

.
Следствие 1. Единственность равновесной цены рAB при неизменной производительной силе общественного труда A и B
При неизменной продуктивности товара A, выражающего свою стоимость, и товара-эквивалента B, существует единственное значение относительной цены товара A, удовлетворяющее условию равенства стоимости товара в относительной форме и стоимости товара-эквивалента, или единственное значение равновесной цены рAB.
Другие значения цены будут неравновесными, так как
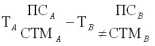
и
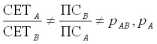
.
Следствие 2. Единственность равновесной цены рBA при неизменной производительной силе общественного труда A и B
Если товар B выражает свою стоимость, а товар A служит эквивалентом, то формула цены B
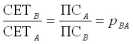
. Так как отношение
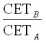
– постоянно, то оно является единственным значением равновесной цены рBA.
Следствие 3. Обратное отношение равновесных цен двух товаров
Между равновесными ценами двух товаров устанавливается отношение
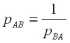
,
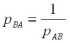
.
Обоснование условия равновесия обмена двух товаров Вальраса
Открытие количественной закономерности
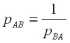
, или условия равновесия обмена двух товаров принадлежит Вальрасу. Модель капитала позволяет дать теоретическое обоснование этой закономерности.
Вторая комбинация простой формы стоимости: изменение производительной силы общественного труда A и B. Законы простого относительного выражения стоимости. Кривая относительной стоимости (цены)
В первой главе Капитала в разделе Простая, единичная или случайная форма стоимости в параграфе Количественная определенность относительной формы стоимости Маркс рассматривает законы простого относительного выражения стоимости 51.
Первый случай – ПРA и СЕТA меняются, ПРB и СЕТB неизменны, в двух вариантах СЕТA падает, СЕТA растет.
Второй случай – ПРA и СЕТA неизменны, ПРB и СЕТB меняются в двух вариантах СЕТB падает, СЕТB растет.
Третий случай – СЕТA (ПРA) и СЕТB (ПРB) изменяются одновременно в одном и том же направлении и в одной и той же пропорции, в двух вариантах СЕТA и СЕТB падают, СЕТA и СЕТB растут.
Четвертый случай – сочетание предыдущих комбинаций.
Приведем простейшую табличную иллюстрацию трех случаев (табл. 2 – 4)..
Таблица 2. Первый случай динамики относительной стоимости
|
t |
СТМA |
ПСA,QA |
ПРA |
СЕТA |
СТМB |
ПСB,Qb |
ПРB |
СЕТB |
ОСЕТA, pAB |
|
СЕТA сокращается, ПРA растет, ПРB и СЕТB – const |
|||||||||
|
1 |
10 |
1 |
0,1 |
10 |
10 |
12 |
1,2 |
0,8 |
12 |
|
2 |
10 |
2 |
0,2 |
5,0 |
10 |
12 |
1,2 |
0,8 |
6 |
|
3 |
10 |
3 |
0,3 |
3,3 |
10 |
12 |
1,2 |
0,8 |
4 |
|
6 |
10 |
6 |
0,6 |
1,7 |
10 |
12 |
1,2 |
0,8 |
2 |
|
12 |
10 |
12 |
1,2 |
0,8 |
10 |
12 |
1,2 |
0,8 |
1 |
Таблица 3. Второй случай динамики относительной стоимости
|
t |
СТМA |
ПСA,QA |
ПРA |
СЕТA |
СТМB |
ПСB,Qb |
ПРB |
СЕТB |
ОСЕТA, pAB |
|
СЕТA и ПРA – const, СЕТB падает, ПРB растет |
|||||||||
|
1 |
10 |
12 |
1,2 |
0,8 |
10 |
1 |
0,1 |
10 |
0,1 |
|
2 |
10 |
12 |
1,2 |
0,8 |
10 |
2 |
0,2 |
5 |
0,2 |
|
3 |
10 |
12 |
1,2 |
0,8 |
10 |
4 |
0,4 |
2,5 |
0,3 |
|
4 |
10 |
12 |
1,2 |
0,8 |
10 |
6 |
0,6 |
1,7 |
0,5 |
|
12 |
10 |
12 |
1,2 |
0,8 |
10 |
12 |
1,2 |
0,8 |
1 |
Таблица 4. Третий случай динамики относительной стоимости
|
t |
СТМA |
ПСA,QA |
ПРA |
СЕТA |
СТМB |
ПСB,Qb |
ПРB |
СЕТB |
ОСЕТA, pAB |
|
ПРA и ПРB растут в одной и той же пропорции, СЕТA и СЕТB сокращаются |
|||||||||
|
1 |
10 |
1 |
0,1 |
10 |
10 |
2 |
0,2 |
5 |
2 |
|
2 |
10 |
2 |
0,2 |
5 |
10 |
4 |
0,4 |
2,5 |
2 |
|
3 |
10 |
4 |
0,4 |
2,5 |
10 |
8 |
0,8 |
1,3 |
2 |
|
4 |
10 |
8 |
0,8 |
1,3 |
10 |
16 |
1,6 |
0,6 |
2 |
|
5 |
10 |
16 |
1,6 |
0,6 |
10 |
32 |
3,2 |
0,3 |
2 |
Вторые варианты не приводятся: их можно получить, взяв обратную последовательность временных периодов.
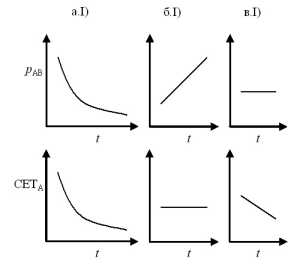
Сравнение динамики относительной цены и стоимости единицы товара по периодам времени показывает, что корреляция имеет место только в первом случае. Во втором случае цена растет, СЕТA неизменна, в третьем – цена неизменна, СЕТA падает (Рисунок 5).
Действительные изменения величины стоимости не отражаются… достаточно ясно и полно в относительном выражении величины стоимости, или в величине относительной стоимости52.
На нижних графиках представлена кривая стоимости единицы товара, на верхних – кривая относительной стоимости (цены) единицы товара. На нижних – динамика стоимости в абсолютном измерении (в ч ОНРВ), на верхних – та же динамика, но в относительном измерении (в количестве ПСB).
Общее соотношение кривой стоимости и кривой относительной стоимости (кривой цены). Циферблат кривой относительной стоимости (цены)
Формула относительной стоимости (цены)
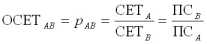
содержит алгоритм построения кривой цены на основе кривой стоимости.
1. Если известно расположение кривой стоимости единицы товара (кривой СЕТ) в координатах Стоимость – Временные периоды, то значения ординат кривой относительной стоимости (цены) с теми же абсциссами на графике в координатах Цена – Временные периоды получаются путем умножения значений точек кривой СЕТ на коэффициент
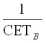
, где B – товар-эквивалент.
2. Если известно расположение кривой СЕТ в координатах Стоимость – Потребительная стоимость, то значения ординат кривой цены с теми же абсциссами на графике в координатах Цена – Потребительная стоимость получаются путем умножения значений точек кривой СЕТ на коэффициент
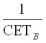
, где B – товар-эквивалент.
Все возможные варианты расположения кривой стоимости единицы товара в координатах СТ – ПС были рассмотрены при анализе комбинаций факторов товара. На циферблате кривой стоимости было показано, что кривая может представлять собой точку или прямую с направленностью от 0 до 360.
Все кривые стоимости на циферблате кривой стоимости превращаются в кривые цены путем умножения значения каждой точки на
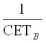
. Полученные таким образом значения цены откладывHются по оси цен, при тех же значениях абсцисс (ПС), что и на графике стоимости (Рисунок 6).
1. Если СЕТB неизменна, то цена рAB пропорциональна стоимости СЕТA. Форма кривой стоимости и ее направленность сохраняется на графике цены с другой осью Y – осью
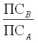
, или рAB. Если принять СЕТB за единицу, то мы получим идентичные графики в двух различных системах координат – СТA – ПСA и рAB – ПСA.
Это правило действует как для относительной, так и для денежной цены. В последнем случае коэффициент, на который умножается значение стоимости единицы товара, равен
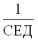
, где СЕД – стоимость денежной единицы.
2. Если СЕТB меняется, то цена рAB или рA не пропорциональна стоимости СЕТA. По сравнению с графиком стоимости график цены деформируется в зависимости от изменения СЕТB или СЕД.
Рассмотрение всех вариантов расположения формы стоимости, или кривой цены в координатах Цена – Временные периоды и Цена A – Потребительная стоимость A – представляет собой объемную математическую задачу, решение которой выходит за рамки учебника.
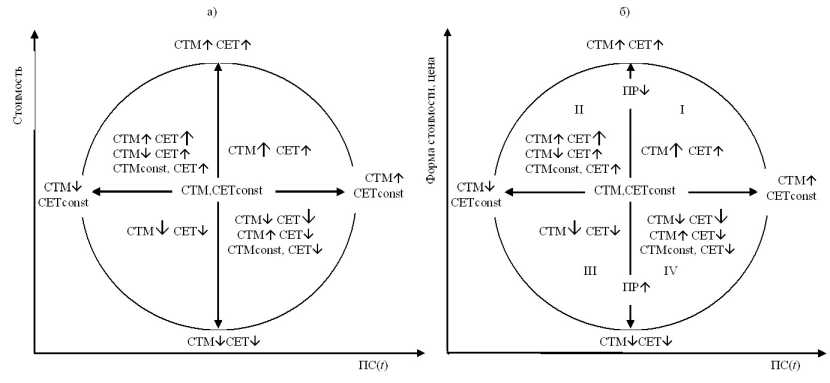
Ограничимся элементарным вариантом – рассмотрением графиков кривой цены при неизменной стоимости единицы товара-эквивалента (стоимости денежной единицы) в координатах СТ – ПС.
Рисунок 6, а воспроизводит циферблат кривой СЕТ, который рассматривался ранее (Рисунок 4). На графике отражены все возможные расположения кривой СЕТ и ее направленность при той или иной комбинации факторов товара – стоимости товарной массы, стоимости единицы товара, потребительной стоимости и производительной силы общественного труда.
Преобразование этого графика в график кривых относительной стоимости или цены (pAB, pA) осуществляется путем умножения каждой точки кривой СЕТ на коэффициент
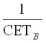
, где B – товар-эквивалент. В условиях денежной формы стоимости коэффициентом служит
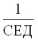
. В нашем элементарном случае СЕТB (или СЕД) принимается за постоянную величину, при том что СЕТB (или СЕД) равна 1 ч ОНРВ.