Подавляющее большинство современных международных корпораций имеют форму ТНК. Статистика ООН насчитывает сегодня примерно 40 000 транснациональных компаний, значение которых в формировании современной мировой экономики является ключевым, ибо они создают реальные предпосылки становления международного производства с единым информационным пространством, международным рынком капитала и рабочей силы, научно-технических услуг.
Транснациональные корпорации контролируют до половины мирового промышленного производства, около 70% внешней торговли. Общая сумма их иностранных инвестиций составляет около 2 трлн. долл. В руках этих компаний находится примерно 95% мировых патентов и лицензий.
Aктивизация деятельности ТНК, наблюдающаяся в настоящее время, придала интеграционным процессам, идущим в мировой экономике, совершенно новый импульс прежде всего потому, что их зарубежные
| ri = |
Ri - Ii |
100 |
| Ii |
где ri- - норма прибыли на i-ю бумагу, %; Ri - прогноз будущей рыночной стоимости ценной бумаги в конце анализируемого периода с учетом дивидендов; Ii - размер первоначальных инвестиций.
Ожидаемая доходность портфеля в этом случае может быть рассчитана как средневзвешенная величина из индивидуальных оценок доходности входящих в портфель ценных бумаг (активов):
| n |
| rp = rifi |
| i = 1 |
где rp - ожидаемая доходность портфеля; fi - доля затрат, инвестируемых в i-ю ценную бумагу; п - число ценных бумаг (активов) в портфеле.
Проиллюстрируем расчет ожидаемой доходности инвестиционного портфеля, используя для этого данные табл. 7.4.
Предположим, что ожидаемая доходность ценных бумаг, входящих в портфель, составит: А - 16,2%; В - 24,6%; С - 22,8%. Тогда
| 3 |
| rp = rifi=16,2 |
| i = 1 |
| 4000 |
| 17200 |
+24,6
| 7000 |
| 17200 |
+22,8
| 6200 |
| 17200 |
=22%
Таблица 7.4. Портфель ценных бумаг
| Ценные бумаги |
Количество ценных бумаг в портфеле |
Начальная рыночная цена одной ценной бумаги , ден. ед. |
Сумма инвестиций, ден. ед. |
| А |
100 |
40 |
4000 |
| В |
200 |
35 |
7000 |
| С |
100 |
62 |
6200 |
| Начальная стоимость портфеля, ден. ед. |
17200 |
||
Из приведенного расчета следует, что инвестор, поставивший перед собой цель - максимизацию доходности, - должен, казалось бы, включить в свой портфель только один вид актива, характеризующийся наивысшей эффективностью (в нашем примере - ценные бумаги В). Однако такой экстремальный подход, совершенно игнорирующий аргумент (показатель) риска, вряд ли можно считать практически приемлемым, так как в реальной действительности наблюдается закономерность роста степени рискованности ценных бумаг с возрастанием их доходности (т. е. имеет место прямая зависимость между этими двумя характеристиками ценных бумаг). Поэтому большинство инвесторов стремятся диверсифицировать свой портфель (не складывать яйца в одну корзину), снижая тем самым риск от потери своих средств при осуществлении портфельных инвестиций.
В качестве показателя степени риска портфельных инвестиций в теории портфеля используется среднее квадратическое отклонение. Для портфеля, состоящего из трех ценных бумаг, формула для расчета среднего квадратического отклонения доходности имеет вид:
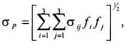
где ij - коэффициент ковариации1 доходностей ценных бумаг i и j.
При осуществлении практических расчетов соответствующие коэффициенты ковариации целесообразно записывать в виде ковариационной матрицы, которая для рассматриваемого нами примера имеет вид (на главной диагонали матрицы располагаются дисперсии доходности ценных бумаг):
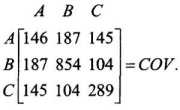
160
Располагая теперь необходимой информацией, рассчитаем степень риска, для рассматриваемого инвестиционного портфеля:
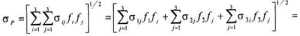
[( 11f1f1+ 12f1f2+ 13f1f3) + ( 21f2f1+ 22f2f2+ 23f2f3) + ( 31f3f1+ 32f3f2+ 33f3f3)]1/2 =
= [(146 0,2325 0,2325 + 187 0,2325 0,4070 + 145 0,2325 0,3605) + (187 0,4070 0,2325 + 854
0,4070 0,4070 + 104 0,4070 + 289 0,3605 0,3605)]1/2 = [227,13]1/2 = 16,65(%)
Оптимизация инвестиционного портфеля. Ожидаемая доходность, и степень риска, рассчитанные для каждого портфеля, позволяют, основываясь на соотношении этих двух параметров, выбрать предпочтительный из анализируемых портфелей.
Проанализируем эту непростую проблему при помощи графической модели, представленной на рис. 7.6.
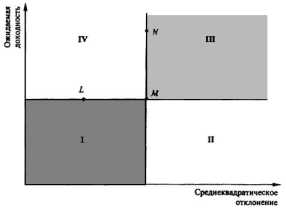
Рис. 7.6. Выбор инвестиционного портфеля
По отношению к представленным на рис. 7.6 инвестиционным портфелям могут быть сделаны следующие выводы:
161
1) портфель L предпочтительнее портфеля М, поскольку оба обладают одинаковой ожидаемой доходностью (rLP = rMP), но портфель L менее рискован, чем М ( LP MP);
2) портфель N является предпочтительнее портфеля М, так как MP = NP, но rNP rMP;
3) те портфели ценных бумаг, которые располагаются в квадранте IV, следует рассматривать как предпочтительные по отношению к портфелю М;
4) те портфели, которые находятся ниже и правее точки М, т. е. в квадранте IV, необходимо рассматривать с точки зрения инвесторов как менее привлекательные нежели портфель М;
5) выбор между портфелями, расположенными в квадрантах I и III, будет зависеть от мнения инвестора относительно доходности и риска с точки зрения допустимого компромисса между этими показателями. Этот компромисс количественно может быть измерен как отношение, показывающее, на какую величину дополнительного риска согласен инвестор за получение дополнительной единицы ожидаемого дохода.
Кривые безразличия. Отношение инвестора к риску и доходности графически может быть представлено с помощью кривых безразличия на двумерном графике, где по оси абсцисс откладывается степень риска ( р), а по оси ординат - доходность портфеля (rp) (рис. 7.7).
Дадим краткие пояснения к рис. 7.7.
1. Инвестор, предпочтения которого представлены на графике а, рассматривает все портфели, характеризующиеся одинаковой степенью риска, как эквивалентные независимо от доходности, которую они обеспечивают. Принимая во внимание, что данного инвестора интересует только риск (точнее, минимизация его), можно сделать вывод: любой инвестиционный портфель, лежащий на кривой безразличия, которая проходит левее других, является более привлекательным по отношению к портфелям, расположенным на кривых безразличия, расположенных правее.
2. Инвестор, интересы которого представлены на графике б, нейтрален к риску; он воспринимает риск как данность и для любой его степени выбирает портфель, максимизирующий доходность.