Естественно, что портфели, отвечающие этому критерию, будут находиться на кривой безразличия I1.
3. График в иллюстрирует промежуточный варинт между первыми двумя: здесь инвестора интересуют как доходность портфеля, так и степень его риска. На дополнительный риск ( p) он готов идти
162
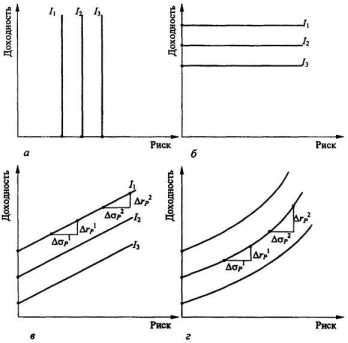
Рис. 7.7. Формализованное отражение предпочтений инвестора
при помощи кривых безразличия
4. График г соответствует более реальной ситуации, суть которой заключается в следующем: с ростом степени риска инвестор готов идти на его дальнейший прирост только за счет все увеличивающегося компенсирующего прироста доходности; для рассматриваемого примера при p1 = p2( rp2 rp1).
Таким образом, можно сделать следующие выводы:
1) все инвестиционные портфели, лежащие на одной кривой безразличия, являются равноценными для инвестора. Следствием этого является тот факт, что кривые безразличия не могут пересекаться1;
2) инвестор будет считать любой портфель, лежащий на кривой безразличия, которая находится выше и левее, более привлекательным, чем любой портфель, лежащий на кривой безразличия, которая находится ниже и правее. В этом также просто убедиться, проведя горизонтальную или вертикальную секущие линии (рис. 7.8);
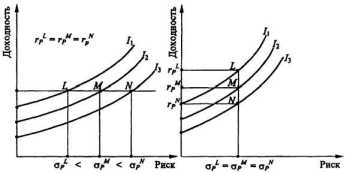
Рис. 7.8. Иллюстрация соотношения кривых безразличия
3) инвестор имеет дело с бесконечным числом кривых безразличия. Это означает, что как бы ни были расположены на графике две из них, всегда существует возможность построить еще произвольное количество непересекающихся кривых безразличия, лежащих между ними.
Выбор оптимального портфеля. Для выбора из множества альтернативных вариантов оптимального инвестиционного портфеля необходимо на одном графике совместить как само допустимое множество анализируемых портфелей, так и множество, или семейство, кривых безразличия, формализующих предпочтения инвестора.
Далее из множества допустимых вариантов необходимо определить инвестиционный портфель, расположенный на кривой безразличия, проходящей выше и левее остальных (рис. 7.9). Для рассматриваемого на рис. 7.9 примера оптимальным будет, очевидно, портфель А.
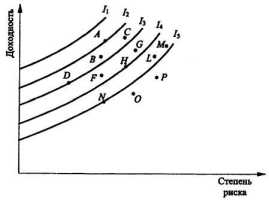
Рис. 7.9. Выбор оптимального инвестиционного портфеля
В заключение еще раз обратим внимание читателя на то, что выбор оптимального инвестиционного портфеля в значительной мере определяется характером расположения кривых безразличия, формализующих предпочтение инвестора относительно соотношения доходности и риска. Так, например, Mсли бы наш инвестор относился к риску более негативно нежели в рассматриваемом случае в качестве оптимального мог бы быть выбран инвестиционный портфель D.
1 В общем случае коэффициент ковариации характеризует зависимость двух случайных величин х и у и
рассчитывается по формуле
| xy = |
|
| (х - х)(у - у) |
, т. е. как среднее арифметическое из произведений отклонений
случайных величин х и у от своих средних х и у. Для рассматриваемого примера положительное значение ковариации показывает, что доходности двух ценных бумаг имеют однонаправленную тенденцию изменения. Отрицательный коэффициент ковариации означает, что анализируемые доходности имеют тенденцию компенсировать друг друга. Например, лучшая, чем ожидалась, доходность одной ценной бумаги сопровождается, как правило, худшей, чем ожидалась, доходностью другой.
Нулевое (или близкое к нулевому) значение коэффициента ковариации означает отсутствие или очень слабую взаимозависимость между доходностями соответствующих ценных бумаг.
1 Убедиться в этом несложно, проведя доказательство от противного, что читателю предлагается сделать самостоятельно.