Первый этап циклического анализа является исключительно важным для достижения конечного успеха и заключается в правильном выборе данных для исследования. Кратко перечислим основные принципы, которыми должны руководствоваться аналитики при отборе ценовой информации для последующего анализа:
В начале исследования должны быть сделаны хотя бы приблизительные предположения о возможных временных характеристиках (период, частота) предполагаемых периодических зависимостей. Основой таких предположений могут быть раз личные доводы, в частности гипотезы о природе циклов, визуальный анализ графиков и пр.
Временной промежуток предстоящего исследования данных должен быть выбран таким образом, чтобы охватывать достаточное для обнаружения периодичности число периодов предполагаемых циклов. С этой точки зрения интервал исследования должен быть как минимум на порядок больше характерного времени предполагаемого цикла. Одновременно период анализа не должен быть чрезмерно велик, так как на слишком больших интервалах в циклах могут случаться многочисленные смещения фаз из-за воздействия различных внешних факторов. Обычно рекомендуется выбирать отрезок исследования порядка 20—30 возможных периодов анализируемых циклов.
Тип временного бара (годовой, квартальный, месячный, не дельный, дневной, часовой и т.д.) исследуемого графика дол жен быть таким, чтобы его длительность была значительно меньше периода предполагаемой цикличности. Невыполнение этого требования, очевидно, приведет к невозможности выделить данный цикл.
Особое внимание должно быть уделено моментам резких изменений рыночных цен. Экстремальные движения на финансовых рынках могут быть вызваны существенным изменением внешних условий, влияющим на параметры цикличности рынка. Таким образом, характеристики циклов до и после данных изменений могут различаться. По этой причине рекомендуется выбирать для исследования участки ценовых графиков, не содержащие необычно резких пиков.
На первом этапе необходимо также качественно охарактеризовать силу и длительность трендовой составляющей движения цен. Присутствует ли на выбранном временном интервале тренд и каково характерное время трендовых изменений в выбранном временном масштабе, можно оценить путем визуальной проверки ценового графика.
Второй этап анализа заключается в предварительной обработке выбранной информации. С отобранными на первом этапе данными обычно производят следующие действия:
Сначала все ценовые данные должны быть переведены в логарифмический масштаб с целью частичного устранения влияния на циклическую составляющую изменения общего уровня цен, которое может происходить в результате трендовых движений. Если не логарифмировать данные, то появятся искажения в амплитуде цикла при высоких и низких уровнях цен.
Далее проводится сглаживание ценового ряда для устранения случайных колебаний. Если предположить, что период случай ной составляющей ценового движения существенно меньше периода предполагаемой циклической составляющей (соответственно, частота случайных колебаний больше частоты пери одических колебаний), то с этой целью можно использовать построение скользящей средней ценовых значений с периодом усреднения не менее характерного времени случайных изменений, но короче периода возможного цикла. В этом случае применение скользящей средней играет роль разновидности методов частотной фильтрации, разделяющих составляющие движений цен с различными частотами колебаний.
Третий этап исследования представляет собой собственно выделение циклической зависимости. Этот этап состоит, во-первых, из более точного, чем на первом этапе, определения вероятных периодов циклов и, во-вторых, из снятия направленности данных, т.е. отделения циклической составляющей от трендового движения цен.
Хотя визуальный анализ ценовых графиков позволяет оценить характерные периоды некоторых циклов, эта оценка является очень приблизительной. Более того, визуально трудно выделить комбинацию нескольких наложенных друг на друга периодических колебаний с разными периодами. Для точной количественной оценки присутствующих в изменениях цен колебаний в настоящее время чаще всего используют спектральный анализ. Метод спектрального анализа заключается в том, что наблюдаемая зависимость изменения исследуемой величины (в нашем случае — рыночных цен) от времени представляется в виде суммы гармонических колебаний с разными частотами. Вклады разных слагаемых данной суммы, как правило, различаются и определяются амплитудой колебаний на определенной частоте. Зависимость такой амплитуды от частоты составляющих гармонических колебаний называется спектром исследуемой временной функции (в нашем случае — функции цены от времени). Разложение исследуемых функций на гармонические составляющие и определение амплитуд этих составляющих требуют большого объема вычислений и проводятся с помощью компьютерных методов.
Если спектр, полученный в результате проведенного анализа, представляет собой горизонтальную прямую, значит, вклады всех частотных составляющих одинаковы. Исследуемая зависимость в этом случае называется белым шумом, в котором нельзя выделить никаких преимущественных колебаний. В том случае, если в полученном спектре некоторым частотам соответствуют существенно более высокие значения, чем соответствующие остальным частотам, можно утверждать, что у исследуемых данных есть циклическая волновая составляющая на данных частотах. Таким образом, пики частотного спектра изменений цен должны соответствовать частотам возможных временных циклов. Однако колебания с экстремальными спектральными значениями не всегда являются статистически значимыми, т.е., проявляясь в течение некоторого числа периодов, они далее могут не повторяться. Следовательно, эти возможные циклические составляющие необходимо подвергнуть соответствующей проверке.
При рассмотрении результатов спектрального анализа необходимо учитывать, что наличие в ценовых движениях трендовой составляющей влияет на форму получающихся спектров и это влияние может серьезно исказить результаты последующих проверок циклов на статистическую значимость. Поэтому, прежде чем приступать к подобным проверкам, из исследуемой зависимости необходимо попытаться удалить трендовую составляющую.
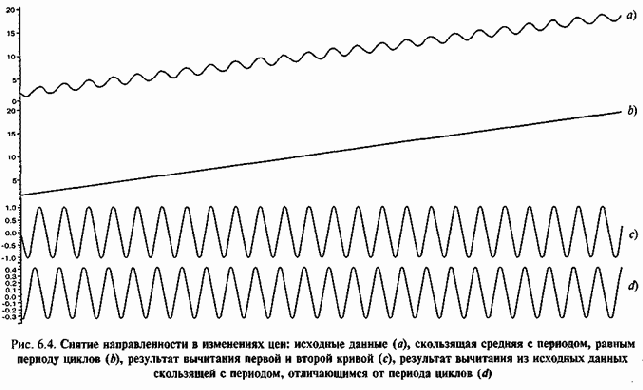
Для удаления из данных трендовой составляющей, или снятия направленности, используют, так же как и в случае удаления случайных колебаний, предполагаемый факт различия характерных периодов изменения трендов и циклов. Поскольку считается, что время трендового движения существенно превышает период предполагаемого цикла, то скользящая средняя с периодом усреднения, близким к периоду цикла, полностью устранит влияние цикличности и в наименьшей степени исказит форму тренда. Такая скользящая средняя отражает только трендовую зависимость, и ее вычитание из исходных данных должно привести к временному ряду, в котором тренд уже отсутствует. Предшествующий этому шагу спектральный анализ необходим для того, чтобы как можно более точно определить период усреднения скользящей средней, поскольку скользящие, усредненные по времени, существенно отличающемуся от времени цикла, будут значительно искажать этот цикл (рис. 6.4).
После проведенного таким образом «снятия» направленности, как правило, снова проводится спектральный анализ и фиксируются скорректированные значения частот возможных циклов.
Проверка статистической значимости циклов с частотами, выявленными при спектральном анализе, представляет четвертый этап циклического анализа. Целью статистической проверки возможного цикла является определение того, насколько случайным является зафиксированное проявление периодичности. Проверка статистической значимости циклов осуществляется стандартными методами математической статистики, и ее результатом, как правило, является величина вероятности случайности цикла. Чем ниже полученное в результате проверки значение, тем меньше вероятность того, что наблюдаемый цикл является случайным. В качестве примеров используемых статистических тестов чаще всего приводят тест Бартелса и тесты, связанные с вычислением F-коэффициента и величины χ2 .
Тест Бартелса сравнивает реальные ценовые ряды и гармоническую кривую с периодом, равным периоду вероятного цикла. Чем точнее совпадение этих двух зависимостей, тем выше считается статистическая надежность такого цикла.
Для проведения следующих тестов необходимо построение так называемой периодограммы — формы расположения данных, часто применяемой в циклическом анализе. Периодограмма представляет собой таблицу, в которой зарегистрированные ценовые данные располагаются в колонках, число которых равно периоду исследуемой циклической зависимости. Число строк данной таблицы определяется длиной исследуемого ценового ряда и показывает, сколько периодов может повторяться в данный вероятный цикл. Обычно для каждой строки и каждой колонки периодограммы вычисляются средние значения.
F-коэффициент для периодограммы равен отношению дисперсии средних значений колонок периодограммы к дисперсии средних значений строк этой периодограммы.
Предполагается, что чем больше значение F-коэффициента, тем более значимым является рассматриваемый цикл. Действительно, при отсутствии в ценовых рядах периодической зависимости с данным периодом средние значения колонок периодограммы не должны существенно различаться между собой. В этом случае дисперсии средних значений колонок и строк периодограммы будут представлять собой близкие величины, а F-коэффициент не должен существенно отличаться от единицы. Если же для исходных данных характерна цикличность, то дисперсия средних значений колонок будет превышать дисперсию средних значений строк исследуемой периодограммы, а F-коэффициент будет существенно больше единицы. Таким образом, величина F-коэффициента может служить мерой статистической значимости анализируемого цикла.
Тест χ2 проверяет статистическую надежность фазы вероятного цикла. В этом тесте строки периодограммы ценового ряда разбиваются на семь равных отрезков и подсчитывается число ценовых максимумов, появляющихся в каждом отрезке в разных строках периодограммы. В случае идеального цикла все максимумы должны попасть в центральный отрезок; будет наблюдаться высокая дисперсия распределения максимумов, а по отрезкам она должна равняться нулю. При отсутствии цикла максимумы должны быть распределены по отрезкам равномерно и дисперсия числа максимумов в отрезках будет низкой. Следовательно, отношение дисперсии числа ценовых максимумов в реальном случае к дисперсии максимумов, вычисленной для полностью случайного поведения цен, также можно использовать для проверки статистической надежности проверяемых циклов.
Методы статистического исследования значимости возможных циклов показывают, как сильно проявляется периодичность среди случайных колебаний цен, и исключительно важны для того, чтобы понять, насколько успешным может быть практическое использование данных закономерностей.