Хотя коэффициент Шарпа — полезный способ измерений, у него есть некоторое количество потенциальных недостатков
1. Измерение прибыли в коэффициенте Шарпа. Это измерение — среднемесячная доходность (или доходность за другой интервал времени), выраженная в процентах годовых, — более приспособлено для оценки вероятной результативности в следующем месяце, чем для оценки результативности на протяжении всего года. Например, предположим, что управляющий в течение полугода получает 40% прибыли каждый месяц, а другие 6 месяцев приносят ему убытки в размере 30%. Вычисляя годовую прибыль, исходя из среднемесячной, мы получим 60% (12 х 5%). Однако если размер позиции корректируется в соответствии с существующими активами, а так поступает большинство управляющих, действительная прибыль за год составила бы -11%. Это произойдет, потому что из каждого доллара активов, имеющихся в начале периода, к концу периода осталось бы только $0,8858((1,40)6 х (0,70)6 = 0,8858).
Как показывает этот пример, если вы озабочены оценкой потенциальной доходности за расширенный период, а не лишь за следующий месяц или другой интервал, то измерение прибыли, используемое в коэффициенте Шарпа, может вести к огромным искажениям. Однако эту проблему можно обойти, используя среднее геометрическое (в противоположность арифметическому) при расчете средней месячной доходности, которую затем выражают в процентах годовых, чтобы получить числитель коэффициента Шарпа. Средняя геометрическая доходность в процентах годовых в точности эквивалентна средней годовой доходности с учетом реинвестиций, которая обсуждается позже в этой главе в разделе, посвященном отношению прибыли к максимальному падению стоимости активов.
2. Коэффициент Шарпа не делает различий между колебаниями стоимости активов вверх и вниз. Коэффициент Шарпа измеряет волатильность, а не риск. А это не обязательно одно и то же.
С точки зрения меры риска, используемой в коэффициенте Шарпа, т.е. стандартного отклонения доходности, колебания вверх и вниз рассматриваются как в равной степени плохие. Таким образом, коэффициент Шарпа показывал бы в невыгодном свете управляющего, у которого спорадически наблюдались бы резкие увеличения активов, даже если бы падения стоимости активов были малы.
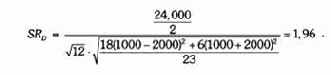
Рис. 21.3 сравнивает гипотетическое движение активов менеджера С, где время от времени наблюдается рост активов и отсутствует их падения, и менеджера D, который столкнулся с несколькими падениями стоимости активов. Хотя оба управляющих зафиксировали равную прибыль за период в целом, и менеджер D столкнулся с несколькими отрицательными переоценками, в то время как у менеджера С их не было, коэффициент Шарпа оценил бы менеджера D выше (см. таблицу). Такой исход — прямое следствие того факта, что коэффициент Шарпа оценивает верхнюю волатильность точно так же, как и нижнюю.
3. Коэффициент Шарпа не делает различий между чередующимися и последовательными убытками. Мера риска в коэффициенте Шарпа (стандартное отклонение) не зависит от последовательности выигрышных и убыточных периодов.
На рис. 21.4 показано гипотетическое изменение стоимости активов с начальной величиной $100 000, управляемых менеджером Е и менеджером F. Каждый из них в обшей сложности зарабатывает $48 000, или $24 000 в год. Однако у менеджера Е месячные доходы в $8000 чередуются с месячными потерями в размере $4000, в то время как менеджер F сразу теряет $48 000 в первые 12 месяцев и последовательно зарабатывает $96 000 в течение оставшегося периода.
Коэффициент Шарпа этих двух управляющих был бы одним и тем же. Несмотря на этот факт, мало нашлось бы трейдеров, рассматривающих деятельность этих менеджеров как эквивалентную с точки зрения риска. Фактически все трейдеры согласились бы с тем, что результаты менеджера F подразумевают значительно более высокий уровень риска.
Рисунок 21.3.
СРАВНЕНИЕ УПРАВЛЯЮЩЕГО С ВЫСОКОЙ ВОЛАТИЛЬНОСТЬЮ, ВЫЗВАННОЙ РЕЗКИМ РОСТОМ АКТИВОВ
ПРИ ОТСУТСТВИИ ПАДЕНИЯ СТОИМОСТИ АКТИВОВ, И УПРАВЛЯЮЩЕГО С ПАДЕНИЯМИ СТОИМОСТИ АКТИВОВ

Рисунок 21 Л.
СРАВНЕНИЕ ДВУХ УПРАВЛЯЮЩИХ С ОДИНАКОВОЙ
ДОХОДНОСТЬЮ И СТАНДАРТНЫМ ОТКЛОНЕНИЕМ, НО С
РАЗЛИЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ МЕСЯЧНЫХ
ПРИБЫЛЕЙ И УБЫТКОВ
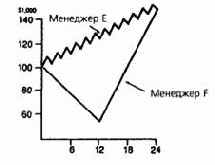
Таблица 21.1.
СРАВНЕНИЕ ЕЖЕМЕСЯЧНЫХ ПРИБЫЛЕЙ ДВУХ УПРАВЛЯЮЩИХ
|
Месяц |
Менеджер С Изменение Совокупное активов изменение активов |
Менеджер D Изменение Совокупное активов изменение активов |
||
|
1 |
0 |
0 |
2000 |
2000 |
|
2 |
1000 |
1000 |
2000 |
4000 |
|
3 |
0 |
1000 |
2000 |
6000 |
|
4 |
0 |
1000 |
2000 |
8000 |
|
5 |
1000 |
2000 |
2000 |
10000 |
|
6 |
0 |
2000 |
-2000 |
8000 |
|
7 |
8000 |
10000 |
2000 |
10000 |
|
8 |
0 |
10000 |
2000 |
12000 |
|
9 |
0 |
10000 |
2000 |
14000 |
|
10 |
0 |
10000 |
-2000 |
12000 |
|
11 |
1000 |
11000 |
-2000 |
10000 |
|
12 |
1000 |
12000 |
-2000 |
8000 |
|
13 |
0 |
12000 |
2000 |
10000 |
|
14 |
0 |
12000 |
2000 |
12000 |
|
15 |
1000 |
13000 |
2000 |
14000 |
|
16 |
0 |
13000 |
2000 |
16000 |
|
17 |
8000 |
21000 |
2000 |
18000 |
|
18 |
0 |
21000 |
-2000 |
16000 |
|
19 |
1000 |
22000 |
-2000 |
14000 |
|
20 |
0 |
22000 |
2000 |
16000 |
|
21 |
0 |
22000 |
2000 |
18000 |
|
22 |
1000 |
23000 |
2000 |
20000 |
|
23 |
0 |
23000 |
2000 |
22000 |
|
24 |
1000 |
24000 |
2000 |
24000 |
Средняя месячная прибыль = 1000
Средняя месячная прибыль = 1000
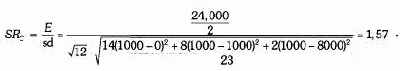
Таблица 21.1. (продолжение)