Шаг 1.
Вычисляются векторы приоритетов альтернатив относительно критериев Кij:
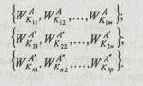
Шаг 2.
Строятся r матриц [Аi], у которых наименованиями строк являются альтернативы, а наименованиями столбцов — критерии Кij . При этом если альтернатива Аi не связана с критерием Kij , то в матрице [Аi] на пересечении соответствующих строки и столбца проставляется нуль.
Шаг 3.
Вычисляются r векторов приоритетов альтернатив WAi (i = 1,r) относительно критериев Кi по выражениям:
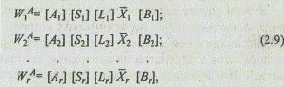
где [Si] — матрица для нормирования матрицы [Аi];
[Li] — структурная матрица для изменения веса альтернатив пропорционально отношению R/N (R — число альтернатив, находящихся под критерием Кij , N — суммарное число альтернатив);

[Bi] — диагональная матрица для получения нормированного вектора WAi, определяемая по выражению (2.9).
Ш а г 4.
Вычисляется вектор приоритетов критериев 
Шаг 5.
Строится результирующая матрица [A0], у которой наименованиями строк являются все рассматриваемые альтернативы
({Аi}, i = 1,т, {А'i}, i = 1,s, {А"i}, i = 1,t),
а наименованиями столбцов — критерии Кi. При этом результирующая матрица [Ао] имеет следующий вид:
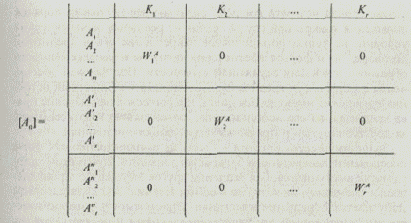
Шаг 6.
Определяется результирующий нормированный вектор приоритетов W0A всех рассматриваемых альтернатив относительно фокуса иерархии К0 на основании известного выражения:
W0A= [А0] [S0] [L0] 
Конец алгоритма.
