Основными составляющими временного ряда являются тренд и сезонная компонента. Составляющие этих рядов могут представлять собой либо тренд, либо сезонную компоненту.
Тренд является систематической компонентой временного ряда, которая может изменяться во времени.
Трендом называют неслучайную функцию, которая формируется под действием общих или долговременных тенденций, влияющих на временной ряд.
Примером тенденции может выступать, например, фактор роста исследуемого рынка.
Автоматического способа обнаружения трендов во временных рядах не существует. Но если временной ряд включает монотонный тренд (т.е. отмечено его устойчивое возрастание или устойчивое убывание), анализировать временной ряд в большинстве случаев нетрудно.
Существует большое разнообразие постановок задач прогнозирования, которое можно подразделить на две группы [24]: прогнозирование односерийных рядов и прогнозирование мультисерийных, или взаимовлияющих, рядов.
Группа прогнозирование односерийных рядов включает задачи построения прогноза одной переменной по ретроспективным данным только этой переменной, без учета влияния других переменных и факторов.
Кроме деления на классы по односерийности и многосерийности, ряды также бывают сезонными и несезонными.
Последнее деление подразумевает наличие или отсутствие у временного ряда такой составляющей как сезонность, т.е. включение сезонной компоненты.
Сезонная составляющая временного ряда является периодически повторяющейся компонентой временного ряда.
Свойство сезонности означает, что через примерно равные промежутки времени форма кривой, которая описывает поведение зависимой переменной, повторяет свои характерные очертания.
Свойство сезонности важно при определении количества ретроспективных данных, которые будут использоваться для прогнозирования.
Рассмотрим простой пример. На рис. 6.2. приведен фрагмент ряда, который иллюстрирует поведение переменной "объемы продажи товара Х" за период, составляющий один месяц. При изучении кривой, приведенной на рисунке, аналитик не может сделать предположений относительно повторяемости формы кривой через равные промежутки времени.
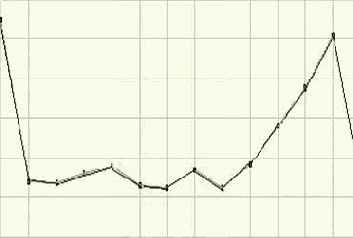
Однако при рассмотрении более продолжительного ряда (за 12 месяцев), изображенного на рис. 6.3, можно увидеть явное наличие сезонной компоненты. Следовательно, о сезонности продаж можно говорить только, когда рассматриваются данные за несколько месяцев.
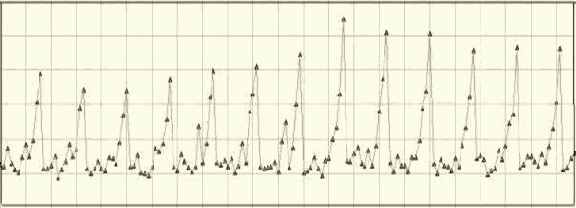
Таким образом, в процессе подготовки данных для прогнозирования аналитику следует определить, обладает ли ряд, который он анализирует, свойством сезонности.
Определение наличия компоненты сезонности необходимо для того, чтобы входная информация обладала свойством репрезентативности.
Ряд можно считать несезонным, если при рассмотрении его внешнего вида нельзя сделать предположений о повторяемости формы кривой через равные промежутки времени.
Иногда по внешнему виду кривой ряда нельзя определить, является он сезонным или нет.
Существует понятие сезонного мультиряда. В нем каждый ряд описывает поведение факторов, которые влияют на зависимую (целевую) переменную.
Пример такого ряда - ряды продаж нескольких товаров, подверженных сезонным колебаниям.
При сборе данных и выборе факторов для решения задачи по прогнозированию в таких случаях следует учитывать, что влияние объемов продаж товаров друг на друга здесь намного меньше, чем воздействие фактора сезонности.
Важно не путать понятия сезонной компоненты ряда и сезонов природы. Несмотря на близость их звучания, эти понятия разнятся. Так, например, объемы продаж мороженого летом намного больше, чем в другие сезоны, однако это является тенденцией спроса на данный товар.
Очень часто тренд и сезонность присутствуют во временном ряде одновременно.
Пример. Прибыль фирмы растет на протяжении нескольких лет (т.е. во временном ряде присутствует тренд); ряд также содержит сезонную компоненту.
Отличия циклической компоненты от сезонной:
1. Продолжительность цикла, как правило, больше, чем один сезонный период;
2. Циклы, в отличие от сезонных периодов, не имеют определенной продолжительности.
Перед началом прогнозирования необходимо ответить на следующие вопросы:
1. Что нужно прогнозировать?
2. В каких временных элементах (параметрах)?
3. С какой точностью прогноза?
При ответе на первый вопрос, мы определяем переменные, которые будут прогнозироваться. Это может быть, например, уровень производства конкретного вида продукции в следующем квартале, прогноз суммы продажи этой продукции и т.д.
При выборе переменных следует учитывать доступность ретроспективных данных, предпочтения лиц, принимающих решения, окончательную стоимость Data Mining.
Часто при решении задач прогнозирования возникает необходимость предсказания не самой переменной, а изменений ее значений.
Второй вопрос при решении задачи прогнозирования - определение следующих параметров:
• периода прогнозирования;
• горизонта прогнозирования;
• интервала прогнозирования.
Период прогнозирования - основная единица времени, на которую делается прогноз.
Например, мы хотим узнать доход компании через месяц. Период прогнозирования для этой задачи - месяц. Горизонт прогнозирования - это число периодов в будущем, которые покрывает прогноз. Если мы хотим узнать прогноз на 12 месяцев вперед, с данными по каждому месяцу, то период прогнозирования в этой задаче - месяц, горизонт прогнозирования - 12 месяцев. Интервал прогнозирования - частота, с которой делается новый прогноз. Интервал прогнозирования может совпадать с периодом прогнозирования. Рекомендации по выбору параметров прогнозирования. При выборе параметров необходимо учитывать, что горизонт прогнозирования должен быть не меньше, чем время, которое необходимо для реализации решения, принятого на основе этого прогноза. Только в этом случае прогнозирование будет иметь смысл. С увеличением горизонта прогнозирования точность прогноза, как правило, снижается, а с уменьшением горизонта - повышается. При выборе интервала прогнозирования следует выбирать между двумя рисками: вовремя не определить изменения в анализируемом процессе и высокой стоимостью прогноза. При длительном интервале прогнозирования возникает риск не идентифицировать изменения, произошедшие в процессе, при коротком - возрастают издержки на прогнозирование.
При выборе интервала необходимо также учитывать стабильность анализируемого процесса и стоимость проведения прогноза.
