Пусть имеется квазистатистика и ее гистограмма и пусть одна из возможных плотностей вероятностной функции распределения, приближающая квазистатистику, обозначается нами как
p(u, À),
где u – значение носителя,
u Î U, À = (x1,…, xN) - вектор параметров распределения размерностью N.
Произведем гипотетический эксперимент. Оценим вид функции распределения p(·), производя вариацию всех параметров вектора À. При этом зададимся критерием правдоподобия нашего распределения – унимодальной гладкой функцией без изломов и разрывов (например, квадратичной многомерной параболой) - и пронормируем значение критерия. Например, если максимум правдоподобия имеет значение L, то вектор параметров À приобретает значение, которое мы будем называть контрольной точкой или точкой ожидания с координатами (x1L,…, xNL) . Мы можем производить нормирование правдоподобия, задавшись некоторым процентом максимума правдоподобия, ниже которого наши вероятностные гипотезы бракуются. Тогда всем правдоподобным вероятностным гипотезам отвечает множество векторов À’, которое в N-мерном фазовом пространстве представляет собой выпуклую область с нелинейными границами.
Впишем в эту область N-мерный параллелепипед максимального объема, грани которого сориентированы параллельно фазовым осям.
Тогда этот параллелепипед представляет собой усечение À’ и может быть описан набором интервальных диапазонов по каждой компоненте
À’’ = (x11, x12; x21, x22;…xN1, xN2) Î À’. (П1.15)
Назовем À’’ зоной предельного правдоподобия. Разумеется, контрольная точка попадает в эту зону , то есть выполняется
x11 £ x1L £ x12,…, xN1 £ xNL £ xN2, (П1.16)
что вытекает из унимодальности и гладкости критерия правдоподобия.
Тогда мы можем рассматривать числа (xi1, xiL, xi2) как треугольные нечеткие параметры плотности распределения, которая и сама в этом случае имеет вид нечеткой функции. А зона предельного правдоподобия тогда есть не что иное, как нечеткий вектор.
Мы видим, что полученное вероятностное распределение имеет не только частотный, но и субъективный смысл, так как зона предельного правдоподобия зависит от того, как мы бракуем вероятностные гипотезы. Представляется, что такое описание всецело отвечает природе квазистатистики, как мы ее здесь вводим. Чем хуже условия для выдвижения правдоподобных вероятностных гипотез, чем тяжелее обосновывать такое правдоподобие, - тем большее значение занимает фактор экспертной оценки. То вероятностное описание, что мы имеем в итоге, - это гибрид, который обещает быть плодотворным.
В качестве примера можно рассмотреть нормальный закон распределения с нечетким среднеквадратическим отклонением (рис. П1.5). Эта нечеткая функция не имеет полосового вида. И тут замое время заметить, что функция с треугольными нечеткими параметрами в общем случае сама не является треугольной и к треугольному виду не приводится.
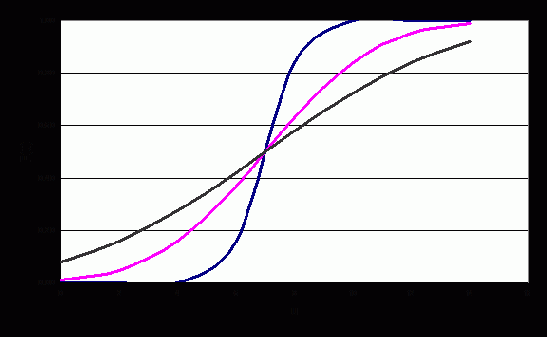
Рис. П1.5. Нормальный закон распределения с нечетким среднеквадратическим отклонением
Зато выполняется нормировочное условие:

где правая часть представляет собой нечеткое число с вырожденной в точку функцией принадлежности.
Интеграл же, не определенный для не четких функций общего вида, представляет здесь предел сумм

Приложим все сказанное к нечеткой оценке параметров доходности и риска фондового индекса. Пусть у нас есть квазистатистика доходностей (r1, …rN) мощности N и соответствующая ей гистограмма (n1,...,nM) мощности M. Для этой квазистатистики мы подбираем двупараметрическое нормальное распределение j(·) с матожиданием m и дисперсией s, руководствуясь критерием правдоподобия

где ri – отвечающее i-му столбцу гистограммы расчетное значение доходности, Dr – уровень дискретизации гистограммы.
Задача (П1.19) – это задача нелинейной оптимизации, которое имеет решение

причем m0, s0 – аргументы максимума F(m,s), представляющие собой контрольную точку.
Выберем уровень отсечения F1 < F0 и признаем все вероятностные гипотезы правдоподобными, если соответствующий критерий правдоподобия лежит в диапазоне от F1 до F0. Тогда всем правдоподобным вероятностным гипотезам отвечает множество векторов À’, которое в двумерном фазовом пространстве представляет собой выпуклую область с нелинейными границами.
Впишем в эту область прямоугольник максимальной площади, грани которого сориентированы параллельно фазовым осям. Тогда этот прямоугольник – зона предельного правдоподобия - представляет собой усечение À’ и может быть описан набором интервальных диапазонов по каждой компоненте
À’’ = (mmin, mmax; smin, smax) Î À’. (П1.21)
Разумеется, контрольная точка попадает в эту зону, то есть выполняется
mmin< m0 <mmax, smin < s0 < smax (П1.22)
что вытекает из унимодальности и гладкости функции правдоподобия.
Тогда мы можем рассматривать числа m = (mmin, m0, mmax), s = (smin, s0, smax) как треугольные нечеткие параметры плотности распределения j(·), которая и сама в этом случае имеет вид нечеткой функции.
