Исследуем некоторую квазистатистику и зададим лингвистическую переменную W = «Значение параметра U», где U – множество значений носителя квазистатистики. Выделим два терм-множества значений: T1 = «U у лежит в диапазоне примерно от a до b» с нечетким подмножеством М1 и безымянное значение T2 с нечетким подмножеством М2, причем выполняется М2 = Ø М1. Тогда функция принадлежности mT1(u) имеет трапезоидный вид, как показано на рис. П1.2.
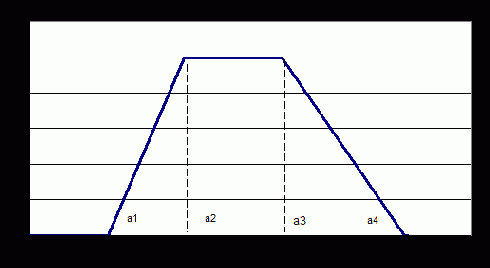
Рис. П1.2. Функция принадлежности трапециевидного числа
Поскольку границы интервала заданы нечетко, то разумно ввести абсциссы вершин трапеции следующим образом:
а = (а1+а2)/2, в = (в1+в2)/2, (П1.5)
при этом отстояние вершин а1, а2 и в1, в2 соответственно друг от друга обуславливается тем, что какую семантику мы вкладываем в понатие «примерно»: чем больше разброс квазистатистики, тем боковые ребра трапеции являются более пологими. В предельном случае понятие «примерно» выраждается в понятие «где угодно».
Если мы оцениваем параметр качественно, например, высказавшись «Это значение параметра является средним», необходимо ввести уточняющее высказывание типа «Среднее значение – это примерно от a до b», которое есть предмет экспертной оценки (нечеткой классификации), и тогда можно использовать для моделирования нечетких классификаций трапезоидные числа. На самом деле, это самый естественной способ неуверенной классификации.