Нечеткая последовательность – это пронумерованное счетное множество нечетких чисел.
Нечеткая прямоугольная матрица – это дважды индексированное конечное множество нечетких чисел, причем первый индекс пробегает M строк, а второй - N столбцов. При этом, как и в случае матриц действительных чисел, операции над нечеткими прямоугольными матрицами сводятся к операциям над нечеткими компонентами этих матриц.
Например,

где все операции над нечеткими числами производятся так, как они введены параграфом выше.
Поле нечетких чисел – это несчетное множество нечетких чисел.
Нечеткая функция – это взаимно однозначное соответствие двух полей нечетких чисел. В наших приложениях область определения нечеткой функции явзяется осью действительных чисел, то есть вырожденным случаем поля нечетких чисел, когда их треугольные функции принадлежности вырождаются в точку с координатами (а, 1).
Нечеткую функцию уместно назвать по типу тех чисел, которые характеризуют область ее значений. Если поле значений – это поле треугольных чисел, то и саму функцию уместно назвать треугольной.
Например , прогноз продаж компании (нарастающим итогом) задан тремя функциями вещественной переменной:
f1(T) – оптимистичный прогноз,
f2(T) – пессимистичный прогноз,
f3(T) – среднеожидаемые значения продаж,
где Т – время прогноза.
Тогда лингвистическая переменная «Прогноз продаж в момент Т» есть треугольное число ( f1(T), f2(T), f3(T) ), а все прогнозное поле есть треугольная нечеткая функция (рис. П1.4), имеющая вид криволинейной полосы.
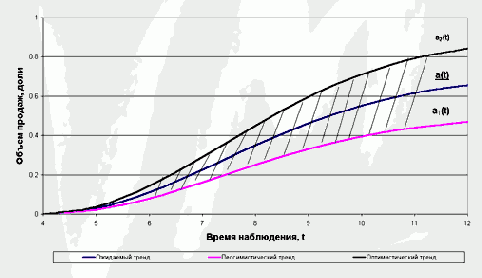
Рис. П1.4. Нечеткий прогноз продаж
Рассмотрим ряд операций над треугольными нечеткими функциями (утверждения приводятся без доказательства):
сложение: сумма (разность) треугольных функций есть треугольная функция;
умножение на число переводит треугольную функцию в треугольную функцию;
дифференцирование (интегрирование) треугольной нечеткой функции проводится по правилам вещественного дифференцирования (интегрирования):

![]() f1(T),
f1(T), 
![]() f3(T) ), (П1.13)
f3(T) ), (П1.13)

![]() f1(T)dT,
f1(T)dT, 
![]() f3(T) dT ), (П1.14)
f3(T) dT ), (П1.14)
функция, зависящая от нечеткого параметра, является нечеткой.
