Исторически первым методом оптимизации фондового портфеля был метод, предложенный Гарри Марковицем в . Суть его в следующем.
Пусть портфель содержит N типов ценных бумаг (ЦБ), каждая из которых характеризуется пятью параметрами:
начальной ценой Wi0 одной бумаги перед помещением ее в портфель;
числом бумаг ni в портфеле;
начальными инвестициями Si0 в данный портфельный сегмент, причем
Si0 = Wi0 ´ ni; (3.10)
среднеожидаемой доходностью бумаги ri;
ее стандартным отклонением si от значения ri.
Из перечисленных условий ясно, что случайная величина доходности бумаги имеет нормальное распределение с первым начальным моментом ri и вторым центральным моментом si. Это распределение не обязательно должно быть нормальным, но из условий винеровского случайного процесса нормальность вытекает автоматически.
Сам портфель характеризуется:
суммарным объемом портфельных инвестиций S;
долевым ценовым распределением бумаг в портфеле {xi}, причем для исходного портфеля выполняется

корреляционной матрицей {rij}, коэффициенты которой характеризуют связь между доходностями i-ой и j-ой бумаг.
Если rij = -1, то это означает полную отрицательную корреляцию, если rij = 1 - имеет место полно положительная корреляция.
Всегда выполняется rii = 1, так как ценная бумага полно положительно коррелирует сама с собой.
Таким образом, портфель описан системой статистически связанных случайных величин с нормальными законами распределения. Тогда, согласно теории случайных величин, ожидаемая доходность портфеля r находится по формуле

а стандартное отклонение портфеля s -

Задача управления таким портфелем имеет следующее описание: определить вектор {xi}, максимизирующий целевую функцию r вида (3.12) при заданном ограничении на уровень риска s, оцениваемый (3.13):

где sM – риск бумаги с максимальной среднеожидаемой доходностью.
Запись (3.14) есть не что иное, как классическая задача квадратичной оптимизации, которая может решаться любыми известными вычислительными методами.
Замечание.
В подходе Марковица к портфельному выбору под риском понимается не риск неэффективности инвестиций, а степень колеблемости ожидаемого дохода по портфелю, причем как в меньшую, так и в большую сторону. Можно без труда перейти от задачи вида (3.14) к задаче, где в качестве ограничения вместо фиксированного стандартного отклонения выступает вероятность того, что портфельная доходность окажется ниже заранее обусловленного уровня.
Если задаваться различным уровнем ограничений по s, решая задачу (3.14), то можно получить зависимость макимальной доходности от s вида
rmax = rmax (s) (3.15)
Выражение (3.15), именуемое эффективной границей портфельного множества, в координатах «риск-доходность» является кусочно-параболической вогнутой функцией без разрывов. Правой точкой границы является точка, соответствующая тому случаю, когда в портфеле оказывается одна бумага с максимальной среднеожидаемой доходностью.
Подход Марковица, получивший широчайшее распространение в практике управления портфелями, тем не менее имеет ряд модельных допущений, плохо согласованных с реальностью описываемого объекта - фондового рынка. Прежде всего это отсутствие стационарности ценовых процессов, что не позволяет описывать доходность бумаги случайной величиной с известными параметрами. То же относится и корелляции.
Если же мы рассматриваем портфель из модельных классов, а ценовую предысторию индексов модельных классов - как квазистатистику, то нам следует моделировать эту квазистатистику многомерным нечетко-вероятностным распределением с параметрами в форме нечетких чисел. Тогда условия (3.12) – (3.13) запиываются в нечетко-множественной форме, и задача квадратичной оптимизации также решается в этой форме. Решением задачи является эффективная граница в виде нечеткой функции полосового вида.
Каждому отрезку на эффективной границе, отвечающей абсциссе портфельного риска, соответствует нечеткий вектор оптимальных портфельных долей.
И, наконец, если нам заданы контрольные нормативы по доходности и риску (бенчмарк модельного портфеля), которые нам следует соблюсти в нашем портфеле, увеличивая доходность и одновременно снижая риск. Если бенчмарк попадает в полосу эффективной границы, то возникает дабл-риск (по факторам доходности и волатильности), что модельный портфель «не переиграет» бенчмарк.
Итак, изложение модифицированного подхода Марковица завершено. Далее по тексту статьи мы считаем, что имеем дело с квазистатистикой модельных индексов в портфеле, которая моделируется нами посредством N-мерного нечетко-вероятностного распределения. Оценив параметры этого распределения как нечеткие числа, мы решаем задачу квадратичной оптимизации в нечеткой постановке, получая эффективную границу в форме криволинейной полосы.
Рассмотрим простейший пример американского модельного портфеля из двух модельных классов: правительственных долгосрочных облигаций (Класс 1, характеризующийся индексом LB Govt Bond) и высококапитализированных акций (Класс 2, характеризующийся индексом S&P500). Сводные данные по обоим индексам приведены в таблице 3.4.
Таблица 3.4. Исходные данные по модельным классам
|
Номер модельного класса |
Ожидаемая доходность r1,2 , % год |
Ожидаемая волатильность s1,2, % год |
||||
|
мин |
средн |
макс |
мин |
средн |
макс |
|
|
1 Облигации |
6.0 |
6.1 |
6.2 |
0.6 |
0.7 |
0.8 |
|
2 Акции |
10 |
12.5 |
15 |
20 |
25 |
30 |
Нам следовало бы еще оценить корреляцию двух индексов. Но, как я покажу далее, в нашем случае этого не потребуется. Пока же для общности обозначим коэффициент корреляции r12.
Надо сразу оговориться, что случай портфеля из двух компонент является вырожденным с точки зрения оптимизации. Здесь полное множество портфельных решений представляет собой участок в общем случае кривой линии на плоскости, и он же является эффективной границей. Так что в настоящем примере мы не сколько решаем оптимизационную задачу, сколько ищем аналитический вид эффективной границы в координатах «риск-доходность».
Запишем (3.12) – (3.13) в частном виде


x2 = 1- x1 (3.18)
Все «постоянные» коэффициенты в (3.16) - (3.17) являются треугольными нечеткими числами. Можно было бы как-то отличить треугольные параметры от обычных скалярных, вводя специальную запись, но, честно говоря, мне не хочется загромождать формулы. И, поскольку в нашем случае s2 >> s1, то имеет место приближенное равенство:

и справедливо

уравнение эффективной границы в виде полосы с прямолинейными границами (см. рис. 3.4).
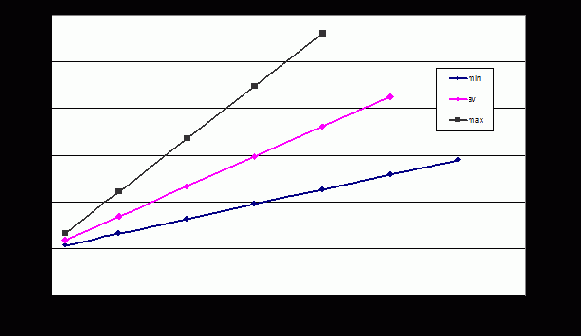
Рис. 3.4. Эффективная граница в виде полосы с линейными границами
Коэффициент пропорциональности в (3.20) есть не что иное, как хорошо известный в портфельном менеджменте показатель Шарпа – отношение доходности индекса (за вычетом безрисковой составляющей доходности) к волатильности индекса. Только в нашем случае он имеет нечеткий вид, сводимый к треугольному по правилу:

В таблицу 3.5 сведены границы для модельного класса облигаций в структуре модельного портфеля для различных уровней риска.
Таблица 3.5. Оптимальная доля облигаций в портфеле
|
Риск портфеля, % год |
1 |
5 |
10 |
15 |
20 |
25 |
30 |
|
|
Доля облигаций в портфеле |
max |
0.967 |
0.833 |
0.667 |
0.500 |
0.333 |
0.167 |
0.000 |
|
av |
0.960 |
0.800 |
0.600 |
0.400 |
0.200 |
0.000 |
0 |
|
|
min |
0.950 |
0.750 |
0.500 |
0.250 |
0.000 |
0 |
0 |
|
|
Разброс |
0.067 |
0.083 |
0.167 |
0.250 |
0.333 |
0.167 |
0 |
|
По краям полосы разброс портфельных границ ниже, чем в середине. Это объясняется тем, что на краях полосы эффективной границы портфель обладает вполне определенным стилем: большей доходности отвечает модельный класс акций, а меньшему риску – модельный класс облигаций.
