Приобретая опцион call, инвестор рассчитывает получить премию как разницу между финальной ценой подлежащего актива ST и ценой исполнения опциона xc. Если эта разница перекрывает цену приобретения опциона zc, то владелец опциона получает прибыль. В противном случае имеют место убытки.
Случайная величина дохода по опциону связана со случайной величиной финальной цены подлежащего актива соотношением [7.2]

В правой части (7.5) все параметры являются известными и постоянными величинами, за исключением ST, которая является случайной величиной с плотностью распределения (7.4).
А текущую доходность по опциону call мы определим формулой

Замечание. Представление (7.2), когда стартовая и финальная цены актива связаны экспоненциальным множителем, является неудобным для моделирования. Аналогичные неудобства вызывает представление доходности на основе степенной зависимости. Именно поэтому мы оперируем категорией текущей доходности как линейной функции дохода и финальной цены. Предполагая нормальность распределения финальной цены актива (что соответствует винеровскому описанию ценового процесса), мы автоматически таким образом приходим к нормальному распределению текущей доходности. Построенная линейная связь текущей доходности и цены является полезной особенностью, которая потом может быть удачно использована в ходе вероятностного моделирования.
Определим плотность jI(y) распределения дохода IT по опциону как функции случайной величины ST. Воспользуемся известной формулой. Если исходная случайная величина X имеет плотность распределения jX(x), а случайная величина Y связана с X функционально как Y=Y(X), и при этом существует обратная функция X=X(Y), тогда плотность распределения случайной величины Y имеет вид [7.6]

В нашем случае, исходя из (7.5),

dST/dIT = 1, IT > -zc. (7.9)
Мы видим, что в точке IT = -zc плотность jI(y) приобретает вид дельта-функции. Необходимо определить множитель при дельта-функции. Это можно сделать косвенным образом. На участке, где функция ST(IT) дифференцируема, в силу (7.7)-( 7.9) выполняется

В силу нормирующего условия справедливо

откуда, в силу (7.10), искомый множитель K есть

Множитель K есть, таким образом, не что иное как вероятность события ST < xc. При наступлении такого события говорят, что опцион call оказался не в деньгах. Это событие – условие отказа от исполнения call-опциона и прямые убытки в форме затрат на приобретение опциона.
Наконец, итоговое выражение для jI(y)

где

На рис. 7. 2 представлен примерный вид плотности вида (7.13).
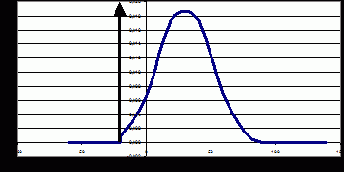
Рис. 7.2. Примерный вид плотности усеченного распределения
Видно, что мы перешли от нормального распределения цен к усеченному нормальному распределению доходов. Но это не классическое усеченное распределение, а распределение, функция которого претерпевает разрыв первого рода в точке с бесконечной плотностью.
Теперь нетрудно перейти к распределению доходности jR(v), пользуясь (7.6), (7.7) и (7.13):

Плотности вида (7.13) и (7.15) – бимодальные функции.
Теперь оценим риск инвестиций в call опцион. Очень подробно виды опционных рисков изложены в [7.7].
Мне думается, что правильное понимание риска инвестиций сопряжено с категорией неприемлемой доходности, когда она по результатам финальной оценки оказывается ниже предельного значения, например, уровня инфляции в 4% годовых для нынешних условий США. Это значение близко к текущей доходности государственных облигаций, и тогда ясно, что обладая сопоставимой с облигациями доходностью, опционный инструмент значительно опережает последние по уровню риска прямых убытков (отрицательной доходности).
Поэтому риск инвестиций в опцион call может быть определен как вероятность неприемлемой доходности по формуле

где jR(v) определяется по (7.15).
Среднеожидаемая доходность вложений в опцион определяется стандартно, как первый начальный момент распределения:

Среднеквадратическое отклонение доходности call опциона от среднего значения также определяется стандартно, как второй центральный момент распределения

Рассмотрим важные асимптотические следствия полученных вероятностных форм. Для этого установим связь между доходностями call опциона и подлежащего актива, с учетом (7.5) и (7.6):

где

Видим, что доходность опциона call и подлежащего актива связаны кусочно- линейным соотношением, причем на участке прямой пропорциональности это происходит с коэффициентом g, который собственно, и характеризует фактор финансового рычага (левериджа). Участок прямой пропорциональности соответствует той ситуации, когда опцион оказывается в деньгах. Поэтому, с приближением вероятности K вида (17.2) к нулю, выполняются следующие соотношения

То есть между соответствующими параметрами подлежащего актива на участке, когда опцион оказывается в деньгах, возникает линейная связь посредством левериджа. С ростом среднеожидаемой доходности актива растет и средняя доходность call опциона, а с ростом волатильности актива растет также и волатильность опциона.
Итак, мы получили вероятностные формы для описания доходности и риска по вложениям в опцион call. Действуя аналогичным образом, мы можем получать подобные формы для опционов другой природы, а также для их комбинаций друг с другом и с подлежащими активами.