Пусть бумага данного вида эмиттирована в момент времени TI по цене N0, причем эта цена может быть как выше, так и ниже номинала (это обусловлено соотношением объявленной купонной ставки и среднерыночной ставки заимствования, с учетом периодичности платежей). Обозначим размер купона DN, а число равномерных купонных выплат длительностью Dt за период обращения обозначим за K, причем для общности установим, что платеж по последнему купону совпадает с моментом погашения бумаги.
Тогда временная последовательность купонных платежей может быть отображена вектором на оси времени с координатами

Формула для справедливой цены процентного долгового инструмента имеет вид:

где

номер интервала, которому принадлежит рассматриваемый момент t,


Моменты ti определяются соотношением (6.22), а внутренняя норма доходности долгового инструмента r отыскивается как корень трансцендентного уравнения вида
С(TI) = N0. (6.27)
Если купон по процентной бумаге нулевой, то переходим к рассмотренному выше случаю дисконтной бумаги.
Анализ соотношений (6.25) и (6.26) показывает, что шум цены, тренд которой имеет вид (6.23), является нелинейно затухающей кусочной функцией на каждом интервале накопления купонного дохода, причем шум получает как бы две составляющих: глобальную – для всего периода обращения бумаги, и локальную – на соответствующем моменту t интервале накопления купонного дохода.
Исследуем характер шума цены процентной бумаги:

где C(t) – тренд цены - определяется по (6.23).
Руководствуясь соображениями, изложенными в предыдущем примере дисконтных бумаг, будем отыскивать СКО шума цены в виде:

![]() (6.29)
(6.29)
где

(6.30)
а i определяется по (6.24). Соотношение (6.30) является частной производной справедливой цены (6.23) по показателю внутренней нормы доходности бумаги с точностью до постоянного множителя.
Аналогично предыдущему примеру, мы можем получить нормировочный делитель для шума цены процентной бумаги. Переход от нестационарного шума к стационарному будет иметь вид:

где 
На рис. 6.3 приведен примерный вид тренда цены процентной бумаги, а на рис. 6.4 – примерный вид СКО такой бумаги.
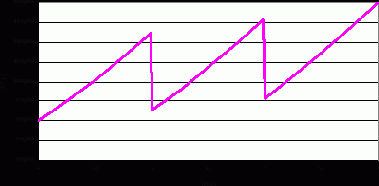
Рис. 6.3. Функция справедливой цены процентной бумаги
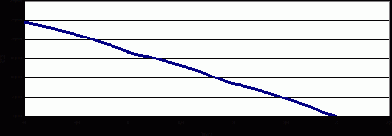
Рис. 6.4. Функция СКО процентной бумаги
Что касается доходности процентных инструментов, то формулы (6.12) – (6.13) получают поправку в виде проплаченного за время Т купонного дохода:

где m – число оплаченных купонов процентной бумаги за период T.
Вывод о том, что случайный процесс 


Рассмотрим расчетный пример.
