Нечеткие описания в структуре метода анализа риска появляются в связи с неуверенностью эксперта, что возникает в ходе различного рода классификаций. Например, эксперт не может четко разграничить понятия «высокой» и «максимальной» вероятности, как это имеет место в. Или когда надо провести границу между средним и низким уровнем значения параметра. Тогда применение нечетких описаний означает следующее:
Эксперт строит лингвистическую переменную со своим терм-множеством значений. Например: переменная «Уровень менеджмента» может обладать терм –множеством значений «Очень низкий, Низкий, Средний, Высокий, Очень высокий».
Чтобы конструктивно описать лингвистическую переменную, эксперт выбирает соответствующий ей количественный признак – например, сконструированный специальным образом показатель уровня менеджмента, который принимает значения от нуля до единицы.
Далее эксперт каждому значению лингвистической переменной (которое, по своему построению, является нечетким подмножеством значений интервала (0,1) – области значений показателя уровня менеджмента) сопоставляет функцию принадлежности уровня менеджмента тому или иному нечеткому подмножеству. Общеупотребительными функциями в этом случае являются трапециевидные функции принадлежности (см. рис. 3.1). Верхнее основание трапеции соответствует полной уверенности эксперта в правильности своей классификации, а нижнее – уверенности в том, что никакие другие значения интервала (0,1) не попадают в выбранное нечеткое подмножество.
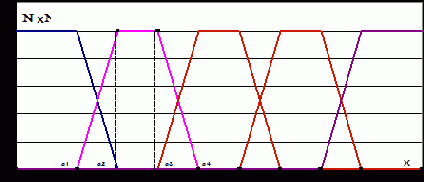
Рис. 3.1. Трапециевидные функции принадлежности
Для целей компактного описания трапециевидные функции принадлежности m(х) удобно описывать трапециевидными числами вида
b(а1, а2, а3, а4), (3.14)
где а1 и а4 - абсциссы нижнего основания, а
а2 и а3 - абсциссы верхнего основания трапеции (рис. 1), задающей m(х) в области с ненулевой принадлежностью носителя х соответствующему нечеткому подмножеству.
Теперь описание лингвистической переменной завершено, и аналитик может употреблять его как математический объект в соответствующих операциях и методах. Продемонстрируем это на примере нашего собственного метода.
