Рассмотрим нашу старую модель изменения цены акций. Пусть каждый день цена меняется на один доллар, но вероятность роста (обозначим ее р) не равна вероятности падения (обозначим ее q). Очевидно, что
p + q = 1.
Предположим, что вы используете стратегию инвестирования, при которой потери обрезаются при падения цены на S долларов (на этой цене стоит «стоп») и акции продаются с прибылью L долларов, если цена достигла этого предела. В теории случайных блужданий (желающим детальнее ознакомиться с этими вопросами мы рекомендуем книги В. Феллера) доказывается, что P(S) — вероятность того, что цена коснется точки S раньше, чем точки L, т.е. вероятность проигрыша

P(L) — вероятность того, что цена коснется точки L раньше, чем точки S, т.е. вероятность выигрыша
P(L) = 1 - P(S).
При такой стратегии ваша средняя прибыль G (в долларах)
G = LP(L) - SP(S).
Анализ этих уравнений показывает, что вариант с различными вероятностями роста и падения цены, когда р ¹ q, качественно отличается от варианта совершенно случайных блужданий, когда р = q. Средняя прибыль равна нулю лишь тогда, когда р = q. Если р ¹ q, средняя прибыль отлична от нуля и, кроме того, вероятности выигрыша или проигрыша начинают зависеть не только от отношения L/S, но и от абсолютных величин L и S. Эти принципиальные моменты, важные для биржевой игры, необходимо рассмотреть подробнее.
Представьте, что вы купили акции по цене 100 долларов за штуку. Данные акции довольно активны, и их цена меняется в среднем на один доллар в день. Вы решаете, что акции могут вырасти до 104 долларов (L = 4), и ставите мысленный предел 104 доллара, когда вы их продадите с прибылью 4%. Для предотвращения больших потерь вы ставите «стоп» на 99 долларов (S = 1), и ваши максимальные потери будут 1 %. Какова вероятность выигрыша Р (L) и какова средняя ожидаемая прибыль G?
Ответ будет зависеть от вероятности р, т.е. от вероятности того, что акции вырастут в цене в течение одного дня. Если р = 0,5 (50% — «случайные блуждания»), то ответ на эти вопросы можно найти в начале данной главы: вероятность выигрыша P(L) = 20 % и средняя ожидаемая прибыль будет равна нулю. А что произойдет, если вероятность р будет равна 0,7 или 0,3? Результаты расчета приведены в таблице 5.2.
Вероятности выигрыша в обоих случаях меньше 60%, хотя средняя прибыль при р = 0,7 положительна и составляет 1,9 долларов, т. е. почти 2%. Это больше, чем средние потери от покупки акций с р = 0,3. Если бы вы купили акции двух компаний с р = 0,7 и с р = 0,3, вложив по 50 % капитала в каждую из них, то средняя прибыль от такого инвестирования составила бы (1,9 - 0,9)/2 = 0,5 % от начального капитала (деление на 2 возникло не из-за усреднения, а потому, что капитал был разделен между двумя компаниями).
Таблииа 5.2.
|
р |
P(L) |
P(S) |
G |
|
0,3 |
0,02 |
0,98 |
-0,9 |
|
0,7 |
0,58 |
0,42 |
1,9 |
Теперь рассмотрим другую важную задачу. Представьте, что вы занимаетесь трейдингом и ваш начальный капитал составляет 100 долларов. Вы покупаете и продаете акции различных компаний, среди которых равновероятно встречаются компании с р = 0,7 и р = 0,3. При этом все деньги, вырученные за продажу очередных акций, вы тратите на покупку следующих, ничего не добавляя и не откладывая. Можно ли получить прибыль при такой стратегии игры? Эта задача близка к методу выбора акций при помощи лука со стрелами, когда вероятности выбора «хороших» и «плохих» компаний практически одинаковы. В таком случае надежду можно возлагать лишь на то, что обрезание потерь «стопами» поможет быстро избавиться от плохих компаний и получить прибыль от хороших. Условия выберем прежние: «стоп» составляет 1 % от стоимости акций, и вы продаете акции, получив 4% прибыли.
Анализ данной задачи аналогичен тому, который был проведен в конце раздела 5.1. Коэффициент роста К вычисляется следующим образом:
К = 1,040,02/2 0,990,98/2 1,040,58/2 0,990,42/2 = 1,008,
т. е. он больше единицы, и средняя прибыль на один трейд составляет около 0,8% (коэффициенты ½ в показателях степени возникли из-за равной вероятности выбора компаний с р = 0,3 и р = 0,7). Через 10 трейдов начальный капитал увеличится в среднем в 1,00810 = 1,083 раз, или на 8%.
Из рассмотренных примеров можно сделать простой вывод: выбирая акции даже случайным образом, можно получить прибыль, если ограничивать потери на случай падения акций, а при их росте дожидаться заметного повышения цены акций. Эта простая истина давно известна на биржах, и мы лишь математически показали, что лежит в ее основе. Но не могут ли рассмотренные модели подсказать оптимальные уровни обрезания потерь и помочь сопоставлению планируемых прибылей с потерями?
Ответ на этот вопрос зависит от распределения вероятностей роста и падения акций. Очевидно, что при растущем рынке практически для всех акций вероятность роста больше, чем вероятность падения. Акции компаний популярной отрасли имеют большую вероятность роста, чем акции других компаний. Опытные инвесторы или трейдеры выбирают акции лучше, чем начинающие, поэтому у выбранных ими акций средние вероятности роста больше 0,5.
Математически это описывается с помощью некоторой функции распределения. Положение максимума этой функции приблизительно совпадает со средней вероятностью роста акций. Учитывая задачу этой книги, мы не будем обсуждать тонкие детали возможных типов распределения, а ограничимся одной простой моделью. Многолетние наблюдения за поведением акций показали, что цена большинства из них колеблется в некоторых пределах, но максимальная вероятность у р, близкого к 0,5. Чем больше р отличается от 0,5, тем реже встречаются такие акции. Наша модель как раз и учтет эту закономерность.
Предположим, что распределение вероятностей роста акций максимально при р = 0,5 и равно нулю при р = 0 и при р = 1. Иными словами, число акций, имеющих 50%-ную вероятность роста за день, максимально, а акций, которые будут падать или расти со 100%-ной вероятностью, не существуют. Между этими значениями функцию распределения для простоты представим линейной, и распределение будет иметь форму равнобедренного треугольника. Если рынок растет, то центр этого треугольника будет смещаться вправо, что означает, что число акций с р > 0,5 превышает число акций с р < 0,5. Треугольная форма распределения остается неизменной, а происходит небольшое его смещение вправо. При падающем рынке число падающих акций превосходит число растущих акций, и наш треугольник будет смещаться влево. Мы проведем расчеты для трех положений центра треугольника — в точках 0,4; 0,5 и 0,6. Эта же модель соответствовать и разным вероятностям выбора «хороших» акций новичками (центр распределения в точке 0,4), средним трейдером или инвестором (центр в точке 0,5) и опытными игроками (центр в точке 0,6).
На основании предложенной модели распределений можно решать практически важную задачу: определить зависимость коэффициента роста К от значений S и L при различных распределениях. Мы рассчитали величины К при разных значениях S и L для трех различных состояний рынка. Полученные результаты приведены на рисунке 5.1 в виде контурных графиков. Точечная линия, проведенная через максимальные значения К указывает на оптимальные значения «стопов» S для различных значений L.
Анализируя данные графики, можно сделать очень важные выводы. Главный из них состоит в том, что если у акций существует распределение вероятностей их роста, то трейдер или инвестор может получить положительную прибыль, опираясь на адекватную стратегию, т.е. разумно планируя ожидаемую прибыль L и правильно расставляя «стопы» S.
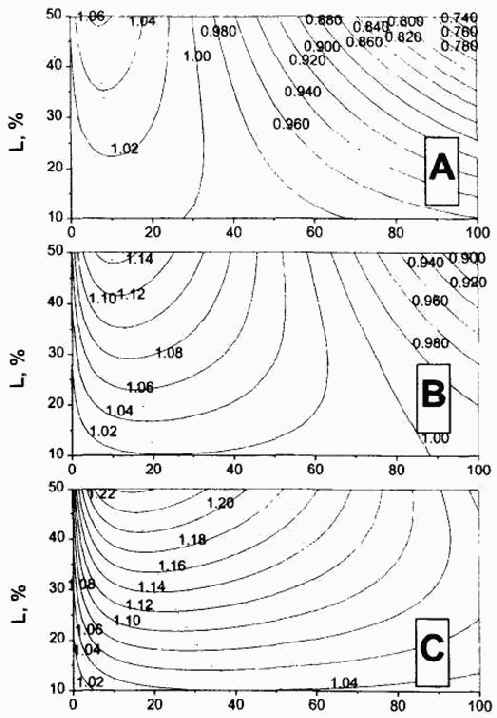
Рис. 5.1. Зависимости коэффициента роста для одного трейда от уровня стоп-заказа S и предела L, при котором акции продаются с прибылью. А — вероятность роста выбранных акций равна 0,4; В — вероятность роста выбранных акций равна 0,5; С — вероятность роста выбранных акций равна 0,6. Эти случаи описывают падающий, стабильный или растущий рынок соответственно. Данный пример также иллюстрирует выбор акций новичками (А), инвесторами с небольшим опытом (В) и профессионалами (С)
Для падающего рынка при игре на повышение «стопы» необходимо ставить как можно ближе к текущей цене акций. Так. например, если вы решили, что акции могут вырасти на 20%, после чего вы их продадите, то «стоп» нужно ставить на уровне 10% от 20% — на уровне 2% от первоначальной цены. При нейтральном рынке «стопы» могут быть немного отодвинуты. При растущем рынке «стопы» могут составлять до 40% от величины намеченной прибыли. Таким образом, если L = 20 %, то стоп может стоять на уровне 8 % от начальной цены акций. Стратегия, в которой «стоп» S равен по величине планируемой прибыли L, самоубийственна: так, при S = L = 50 % даже при нейтральном рынке трейдер будет терять на каждом трейде около 10% капитала. Трейдинг с большими планируемыми прибылями вообще опасен, здесь особенно важен выбор «стопов»: чем больше L, тем ближе должен быть «стоп» к текущей цене.
Как уже было отмечено, такая же модель описывает и распределение выбора акций биржевыми игроками разной квалификации. Начинающие игроки чаще выбирают неудачные акции, и их единственная возможность сохранить инвестиционный капитал — расстановка очень близких «стопов». Более опытные игроки, которые выбирают акции с большей вероятностью роста, могут позволить себе поставить «стопы» подальше.
Рассмотрим еще некоторые закономерности, сопутствующие покупке акций, у которых вероятность роста р отличается от вероятности падения q. В приведенных ранее примерах мы предполагали, что дневное изменение цены акций равнялось одному доллару. А что изменится, если изменение цены за день будет меньше, например, 0,5 или 0,25 доллара? Как изменятся вероятности выигрыша и проигрыша, средняя прибыль и продолжительность одного трейда? Обозначим изменение цены за день через АХ. Результаты расчетов для различных АХ при фиксированных величинах предела L = 4 и «стопа» S = 1 показаны в таблице 5.3.
Таблииа 5.3.
|
р |
АХ |
P(L) |
P(S) |
G |
|
0,3 |
1 |
0,02 |
0,98 |
-0,9 |
|
0,3 |
0,5 |
0,00 |
1,00 |
-1,0 |
|
0,3 |
0,25 |
0,00 |
1,00 |
-1,0 |
|
0,7 |
1 |
0,58 |
0,42 |
1,9 |
|
0,7 |
0,5 |
0,82 |
0,18 |
3,1 |
|
0,7 |
0,25 |
0,97 |
0,03 |
3,8 |
Результаты, как видим, поразительны. При уменьшении изменения цены акций резко вырастают вероятности выигрыша при р = 0,7. При этом величина проигрыша при р = 0,3 остается неизменной, так как она ограничена уровнем «стопа», а выигрыш при р = 0,7 растет, асимптотически стремясь к величине своего предела L = 4. Единственный недостаток в таком случае — не отраженное в таблице резкое увеличение средней продолжительности трейда.
Таким образом, если изменение цены акций происходит более мелкими шагами, то при р > 0,5 вероятность выигрыша и величина прибыли заметно возрастают. Однако в таком случае инвестору надо быть готовым к длительному ожиданию запланированной прибыли.
Есть еще одна интересная закономерность, связанная с уменьшением кванта изменения цены акций. Чтобы выявить ее более четко, проведем вычисление вероятности срабатывания «стопа» при р = 0,4 в случае S = L = 1. Такую ситуацию можно представить в случае длительного роста акций, когда вероятность падения цены уже больше, чем вероятность ее роста. Трейдер хочет попробовать «вытянуть» последний доллар прибыли и пододвигает «стоп» как можно ближе к текущей цене акций. Его решение таково: если цена поднимется еще на доллар, то акции надо продавать. Если же цена упадет на доллар, то акции автоматически будут проданы «на стопе». Какова вероятность P(S), что сработает «стоп»? Ответ можно получить из таблицы 5.4.
Таблица 5.4.
|
DX |
Р(S) |
|
1 |
0,6 |
|
0,5 |
0,69 |
|
0,25 |
0,84 |
|
0,1 |
0,98 |
Вывод простой: при «вытягивании» последнего доллара, когда вероятность падения цены уже больше, чем вероятность ее роста, шанс потерять доллар резко возрастает с уменьшением кванта изменения цены акций. Иными словами, если акции выросли в цене до предела, который вы планировали для выхода, а далее изменение цены стало происходить малыми квантами, то лучше продать акции, не испытывая судьбу: вероятность выигрыша очень мала. Здесь уместно привести слова отца бывшего президента США Джона Кеннеди — Джо Кеннеди, который в свое время был известным трейдером на Уолл-стрит. Он сказал: «Только глупец держит (акции), чтобы получить последний доллар».
В этом месте нелишне напомнить о неизменно полезной диверсификации, которая осуществляется разбиением капитала между акциями нескольких компаний. Она эффективна и в данном случае, но только следует иметь в виду, что разбиение капитала, резко уменьшая вероятность потерь, приводит к некоторому уменьшению коэффициента роста.
И еще надо осознавать, что выводы, которые мы сделали на основе анализа различных моделей рынка, относятся к моделям, а не к реальному рынку. Данные модели были рассмотрены не для получения конкретных цифр, которые можно использовать для планирования прибыли или расстановки «стопов», а для иллюстрации общих принципов трейдинга и важности выбора правильной стратегии.
Отметим также, что планируемая прибыль и «стопы» должны выбираться не на основе слепого следования каким-либо принципам — например, 20% прибыли и 5% допустимых потерь, а с учетом поведения конкретных акций и текущей ситуации на рынке. В течение трейда уровень «стопов» не должен быть фиксирован — по мере изменения цены акций он должен перемещаться. Планируемую прибыль иногда тоже можно и нужно менять. Рынок требует от трейдера большой гибкости, тем не менее, перед началом каждого трейда нужно четко представлять, что вы хотите получить от данных акций и что будете делать, если ваши предположения не оправдаются. Вот на этом этапе планирования и могут пригодиться идеи, описанные в данной главе.
Приведенные примеры, возможно, вселили в вас оптимизм и смутное чувство, что деньги на бирже делаются легко: надо только ставить «стопы» и дожидаться хорошей прибыли в случае удачного выбора акций. Если бы все было так просто, кто бы проигрывал?! Мы не будем приводить результаты более полного анализа реальных ситуаций, а только скажем, что прибыль, которая получается с использованием слепой стратегии (к примеру, X % прибыли и Y % допустимых потерь), очень небольшая. Из завершающейся главы вы, например, можете сделать вывод, что наилучшей стратегией является расстановка близких «стопов» и ожидание больших прибылей. Однако перед покупкой акций необходимо взвесить реальность получения высокой прибыли для данных акций. Безусловно такие акции есть, но ожидать в короткое время высокой прибыли порядка 30 — 50 % от всех акций было бы наивно и разорительно. В дальнейшем мы рассмотрим, как можно оценивать наиболее вероятную прибыль для конкретных акций. И еще всегда нужно учитывать, — особенно если вы играете небольшой суммой, — что потери на комиссионных, на разнице между покупной и продажной ценой и на других накладных расходах (платные источники информации, телефонные разговоры и т.п.) могут «съесть» ваши прибыли. Методы, описанные в данном разделе, лучше рассматривать не как рецепты получения сверхприбылей, а как способы страховки от разорительных потерь. Для хороших прибылей, существенно превышающих среднее изменение цен акций на рынке, необходимо постоянно искать перспективные акции, у которых вероятность роста устойчиво превышает вероятность падения. Тут важен каждый процент, и вам нужно научиться определять вероятность роста акций.
