Стоимость облигации определяется как настоящая стоимость ожидаемого денежного потока.
Введем обозначения:

Рассмотрим пример. Допустим, купонная ставка по облигации номинала в 1000 рублей составляет 15%. Срок до погашения облигации 15 лет. Необходимо оценить стоимость облигации в момент выпуска, через 1 год после выпуска, через 2 года, через 5 лет.
Результаты расчетов сведены в таблицу 4. Приведем графическую интерпретацию полученных результатов на рисунке 3. В качестве параметра t использован показатель времени, прошедшего с момента эмиссии облигации.
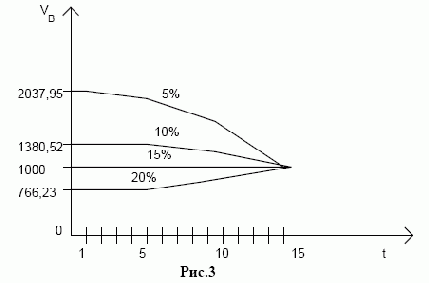
Проанализируем таблицу 7 (приложение1) и график на рис. 3.
1. Всегда, когда купонная ставка совпадает с текущей курсовой ставкой, теоретическая оценка облигации совпадает с номинальной стоимостью. Как правило, в момент выпуска облигации купонная ставка устанавливается на уровне текущей курсовой ставки.
2. В случае, когда текущая курсовая ставка выше, чем купонная ставка, цена облигации становится ниже номинала. В этом случае говорят, что облигация продается с дисконтом.
3. В случае, когда текущая курсовая ставка ниже, чем купонная ставка, цена облигации становится выше номинала. В этом случае говорят, что облигация продается с премией.
4. Рыночная стоимость облигации стремится с приближением даты
погашения к номиналу.
Проведем дальнейший анализ таблицы 7 и сделаем выводы.
1. При фиксированной купонной ставке и изменяющейся текущей курсовой ставке возрастание текущей курсовой ставки приводит к снижению влияния купонной ставки на оценку облигации.
2. В целом влияние купонной ставки на оценку облигации снижается с приближением срока погашения облигации, влияние номинала возрастает в этой ситуации.
3. Чем больше купонная ставка при заданной текущей курсовой ставке, тем выше оценка облигации, при меньшей курсовой ставке оценка облигации изменяется резче (кривая с меньшей купонной ставкой "круче" и расположена ниже кривой с большей купонной ставкой).
На знании этих закономерностей основывается разумное поведение инвестора при управлении своим портфелем.
Экономическая интерпретация данной формулы (18) очевидна. В самом деле, допустим, выпускается некая облигация в момент времени t. Очевидно, что купонная ставка в этот момент устанавливается примерно равной ставке, существующей в данном экономическом пространстве (например, ставке рефинансирования). Допустим, ставка рефинансирования падает, в этом случае доход, приносимый облигацией, становится больше, чем если бы эта сумма была помещена на депозит в банк, отсюда и рост цены облигации. Предпочтительнее покупка облигации. В противном случае, при росте ставки рефинансирования наблюдается, с точки зрения инвестора, "бегство от облигаций", приносящих более низкий доход по сравнению хотя бы с помещением данной суммы на банковский депозит.
Содержание раздела
