Индексные методы измерения экономических процессов

В экономическую активность вовлечено очень боль­шое число участников и ней так или иначе обращается множество разнообразных материальных и финансовых активов. Измерить все это с помощью небольшого набо­ра чисел - непростая задача. Но необходимая, если мы хотим иметь какие-то объективные методы прогнозиро­вания и планирования операций в этой экономической среде. Умение читать и понимать экономические данные - это и наука и искусство, владение которыми необходи­мо для трейдера валютных рынков. Поэтому мы рассмот­рим здесь некоторые основные определения и понятия, связанные с количественным измерением экономических процессов.
Прежде всего, следует отметить, что для многих эко­номических параметров важным бывает не столько само значение, сколько его изменение за прошедший проме­жуток времени. В экономической статистике использует­ся несколько способов записи изменения количественных параметров. Обозначим Xt числовое значение некоторо­го экономического параметра (цены, объема выпуска и т.д.) в момент времени t (день, месяц, квартал, год). Не­который момент, выбранный в качестве начала измере­ний, мы обозначаем t = 0, а затем считаем время целыми единицами: t = 1,2, 3,... .Величину изменения параметра Х за промежуток времени от t до t+1 обозначим

ΔXt=Xt+l-Xt.

Если, например Xt измеряет выпуск продукции за месяц t, то ΔXt - прирост выпуска за месяц t+1, если Xt - цена, то ΔXt - изменений цены, имевшее место в течение меся­ца t+1.
Очень часто нас интересует не сама величина изме­нения параметра X, а насколько это изменение велико по отношению к имевшемуся значению; тогда мы использу­ем процентные величины изменений:

(Xt+l/Xt-l)100(%).

Общепринятая форма представления процентных из­менений - годовые проценты (annualized). Предположим, валютный курс Х
изменился за месяц с 1.6205 до 1.6510, АХ1 = X1 – Х0 = 0.0305; в процентном виде это будет

( X1 / X0 - 1 )100 = 1.88 %.

На сколько изменится валютный курс концу года, если этот темп будет сохраняться каждый месяц? Ответ дает­ся известной формулой сложных процентов:

( 1 + ( X1 / X0 - 1 ))¹² - 1 = 0.25076



или 25.08 %. Это означает, что ежемесячный прирост на 1.88 % эквивалентен годовому росту 25.08 %, то есть 25.08% - это и есть 1.88 ежемесячных процентов, представ­ленные в виде годовых процентов (annualized).


Рассмотрим пример пересчета квартального показа­теля: пусть рост ВВП за первый квартал составил 1.9%; каков будет годовой рост при сохранении этого темпа? По формуле сложных процентов имеем,

( 1 + 0.019 )⁴ - 1 = 0.07819, или 7.82 %.

При анализе экономических данных следует иметь ввиду, что многие индикаторы экономической статисти­ки, публикуемые в информационных системах, проходят предварительную обработку, направленную на удаление сезонной зависимости (seasonality), которая может иска­жать тенденции экономического роста. Имеется много причин, по которым различные виды экономической ак­тивности зависят от времени года, а соответствующие им индикаторы каждый год повторяют похожую картину. Например, строительная активность сильно зависит от погоды, а значит и от сезона; перед новогодними празд­никами каждый год происходит рост объемов розничной торговли; производители автомобилей обычно именно летом переходят на производство новых моделей, так что в это время объем выпуска регулярно может снижаться; компании по сбору налогов, в соответствии с законода­тельством, имеют определенные временные рамки, как и выплаты доходов. Явно выраженная зависимость от вре­мени года видна на примере графиков валового внутрен­него продукта Японии (Рис.8.2), жилищного строитель­ства (Рис. 13.1) и объема продаж новых автомобилей США (Рис. 13.3).
Подобная сезонная зависимость может затруднять обнаружение тенденций экономического роста. Поэтому разработаны специальные методики, позволяющие на основе статистики предыдущих лет выделить регулярно повторяющиеся колебания показателя и сгладить его гра­фик, чтобы можно было оценить именно тенденции ус­тойчивого роста.

Сезонно выровненные данные
сопровож­даются при публикации дополнительным индексом SA (seasonally adjusted) (на рисунке 13.3. тот же показатель продаж новых автомобилей представлен для иллюстра­ции в сезонно сглаженном виде, то есть после сезонного выравнивания). Более подробно с методами сезонной обработки экономических временных рядов можно по­знакомиться при необходимости по книге Эддоуса и Стэнсфилда, указанной в списке литературы.
Отдельно рядом с показателем при публикации ука­зывается, к какому периоду относится его значение: М -месяц, Q - квартал, Y - год. Часто бывает так, что публи­куемое значение показателя приводится в виде его отно­шения к значению этого показателя за соответствующий период предыдущего года; тогда оно будет сопровождать­ся меткой Y/Y. Соответственно - Q/Q означает кварталь­ные данные по отношению к предыдущему кварталу, а М/М - данные за месяц по отношению к предыдущему месяцу.


Многие экономические показатели относятся сразу к большой группе объектов, например индекс потреби­тельских цен есть изменение цен некоторой выбранной группы товаров и услуг (потребительской корзины). По­строение таких индексов осуществляется следующим об­разом: пусть

p0(l),p0(2),...,p0(N)

цены товаров и услуг в начальный момент времени либо в предыдущий период, а

pl(l),pl(2),...,pl(N)

их цены через t = 1 и пусть

q0(l),q0(2),..„q0(N), ql(l),ql(2),...,ql(N)

соответствующие количества товаров и услуг, входящих в потребительскую корзину в начальный момент време­ни и через время t = 1.
Тогда в качестве индекса, показывающего измене­ние цен потребительской корзины за время t, может быть взято отношение

pl(l)*ql(l) + pl(2)*ql(2) +...+pl(N)*ql(N)
I = ————————————————————————————.
p0(l)*q0(l) + p0(2)*q0(2) +...+p0(N)*q0(N)

Такие индексы также записывают и в процентном виде.
Приведенный выше индекс учитывает как изменение цен, так и изменение состава потребительской корзины (индекс Пааше). Существуют индексы (называемые ин­дексами Ласпейреса), которые строятся исходя из пред­положения о неизменности состава потребительской кор­зины:

pl(l)*q0(l) + pl(2)*q0(2) +...+pl(N)*q0(N)
I = —————————————————————————————.
p0(l)*q0(l) + p0(2)*q0(2) +...+p0(N)*q0(N)

Эти индексы измеряют только влияние происшедших из­менений в ценах.
Многие используемые в статистике валютных рын­ков индексы строятся по таким формулам, иногда с теми или иными изменениями. Например, часто применяются так называемые «реальные» показатели экономики. Смысл их состоит в том. что фиксируются цены на неко­торый момент времени, а объем выпуска (или состав по­требительской корзины) изменяется в течение данного промежутка времени. Реальный показатель учитывает рост объемов выпуска (потребления), а рост цен на него не оказывает влияния, то есть, реальные показатели «сво­бодны от инфляции».

Для того чтобы избежать подобных неоправданных скачков, поступают следующим образом: сумма цен но­вых акций делится не на их количество, а на некоторый знаменатель x, который выбирается из условия, что ин­декс откроется «сегодня» с тем же значением, с которым он закрылся вчера:

( А + В + D ) / x = 20,

откуда получаем, x = (25 + 18 + 17 ) / 30 = 2,0 . Это значе­ние x фиксируется и используется затем в качестве знаме­нателя до тех пор, пока не произойдет новое изменение в составе акций индекса. При этом, значение знаменателя x (divisor) является само по себе индикатором фондового рынка и публикуется в средствах массовой информации наравне с индексами Доу-Джонса.



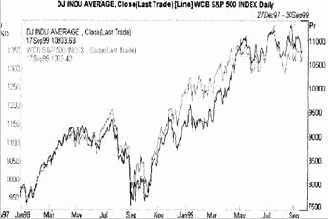
Рис. 4.3. Промышленный индекс Доу-Джонса, и фондовый индекс S&P 500

Индекс Доу-Джонса является, по всеобщему призна­нию, эффективным индикатором динамики поведения фондового рынка США; он наглядно показывает имен­но движения рынка, изменение его настроений. Но есть у него и некоторые недостатки - сама по себе величина ин­декса не отражает цен акций, хотя и строилась в виде сред­ней цены: но ведь нет акций, торгующихся по 11000$! К тому же количественный состав акций, входящих в спи­сок индекса весьма невелик, особенно по сравнению с изобилием наименований акций, обращающихся на фон­довом рынке США. Из-за этого его поведение может да­вать искаженную картину развития рынка в целом. Это дало основание бывшему председателю Федеральной Ре­зервной Системы Volcker'y при очередном обсуждении возможной угрозы, которую представляет переоцененный рынок американских акций для экономики США, заме­тить, что судьба американской экономики зависит от 50 акций, из которых половина никогда не докладывали о каких-либо прибылях.
Поэтому для более объективного оценивания дина­мики фондового рынка применяют разные индексы, в частности в США широко распространен индекс Standard and Poors 500 (S&P500), который отслеживает 500 акций основных корпораций производственного сектора и его значение равно средневзвешенной цене этих акций. Ина­че говоря, для вычисления S&P500 используется та же формула, по которой считался торгово взвешенный ин­декс доллара, но в качестве Pi берется цена акции, a wi -ее капитализация, то есть выраженная в долларах цена того количества акций i, которые обращаются на рынке. На рисунке 4.3. индексы Доу-Джонса и S&P500 изобра­жены рядом для сравнения.
Ниже в качестве иллюстрации статистики фондово­го рынка приведены графики английского фондового ин­декса FTSE и японского фондового индекса NIKKEI.


Отслеживание поведения фондовых индексов явля­ ется обязательной частью аналитической работы валют­ного трейдера, поскольку спрос на акции, номинированные в конкретной валюте, может очень сильно сказаться на курсе этой валюты. Так, летом 1999 года даже посто­янные интервенции Банка Японии, на которые он потра­тил более 20 миллиардов долларов, не смогли остановить укрепления йены, поскольку одним из сильнейших дей­ствовавших в это время факторов был высокий спрос на японские акции. На рисунке 4.5. хорошо видно, как с на­чала 1999 года японские акции прекратили затяжное па­дение и начали расти в цене. Инвесторы из Европы, Ве­ликобритании и США конвертировали значительные сум­мы в йену с целью приобретения японских акций, и это постоянно поднимало курс йены по отношению к доллару.



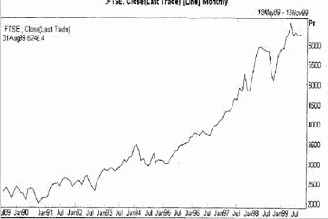
Рис. 4.4. Британский, индекс фондового рынка FTSE



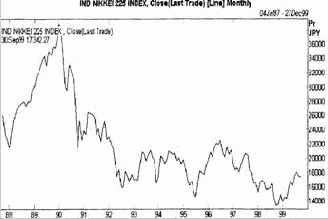
Рис. 4.5. Японский индекс фондового рынка Nikkei

Содержание раздела

---