Все сказанное по поводу одиночной длинной опционной позиции остается верным и для одиночной короткой опционной позиции. Единственное отличие заключается в ином написании уравнения (5.14):
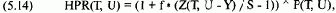
где HPR(T, U) = НРR для данного тестируемого значения Т и U;
f = тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равна
U - Y, а время, оставшееся до срока истечения, равно Т,
Р(Т, U) = вероятность того, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполнения, равно Т;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Для одиночной короткой опционной позиции это уравнение преобразуется в:
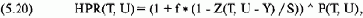
где HPR(T, U) == HPR для данного тестируемого значения Т и U;
f= тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y)= теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т;
Р(Т, U) = вероятность того, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполнения, равно Т;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Обратите внимание, что единственным отличием уравнения (5.14) для одиночной длинной опционной позиции от уравнения (5.20) для одиночной короткой позиции является выражение (Z(T, U-Y)/S-1), которое заменяется на (1-Z(T, U - Y) / S). Все остальное в отношении одиночной длинной опционной позиции верно и для одиночной опционной короткой позиции.
Содержание раздела
