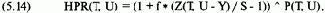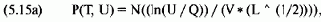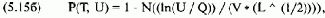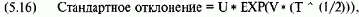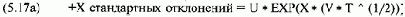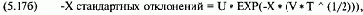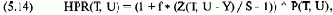Одиночная длинная позиция по опциону и оптимальное f
Рассмотрим обычную покупку колл-опциона. Вместо того чтобы для нахождения оптимального f использовать полную историю сделок по опционам данной рыночной системы, мы рассмотрим все возможные изменения цены данного опциона за время его существования и взвесим каждый результат вероятностью его осуществления. Этот взвешенный по вероятностям результат является HPR, соответствующим цене покупки опциона. Мы рассмотрим весь спектр результатов (т.е. среднее геометрическое) для каждого значения f и таким образом найдем оптимальное значение. Почти во всех моделях ценообразования опционов вводными переменными, имеющими наибольшее влияние на теоретическую цену опциона, являются: (а) время, оставшееся до истечения срока, (б) цена исполнения, (в) цена базового инструмента и (г) волатильность. Некоторые модели могут иметь и другие вводные данные, но именно эти четыре переменные больше всего влияют на теоретическое значение. Из этих переменных две — время, оставшееся до истечения срока, и цена базового инструмента — переменные величины.
Волатильность тоже может изменяться, однако редко в той же степени, что цена базового инструмента или время до истечения срока. Цена исполнения не изменяется.
С помощью нашей модели можно найти теоретическую цену для всех значений цен базового инструмента и времени, оставшегося до истечения срока. Таким образом, HPR для опциона является функцией не только цены базового инструмента, но и функцией времени, оставшегося до даты истечения опциона:
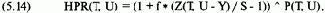
где f = тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т. Эту цену можно определить с помощью любой модели ценообразования, которую пользователь посчитает подходящей;
Р(Т, U) = 1-хвостая вероятность того, что цена базового инструмента равна U, когда время, оставшееся до истечения срока исполнения, равно Т. Это значение можно определить из любой формы распределения, которую пользователь посчитает подходящей;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
С помощью этой формулы можно рассчитать HPR (взвешенное по вероятности результата) по сделке с опционом, при условии, что через время Т цена базового инструмента будет равна U. В данном уравнении переменная Т представляет собой долю года (выраженную десятичной дробью), оставшуюся до истечения срока опциона. Поэтому на дату истечения Т = 0. Если до истечения срока остается один год, то Т = 1. Переменная Z(T, U - Y) зависит от модели ценообразования, которую вы используете. Единственная переменная, которую вам надо рассчитать, — это Р(Т, U), т.е. вероятность того, что базовый инструмент будет равен U при заданном Т (т.е. времени, оставшемся до конца действия опциона). Если использовать модель Блэка-Шоулса или модель товарных опционов Блэка, то можно рассчитать Р(Т, U) следующим образом:
если U < или = О:
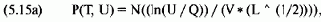
если U > Q:
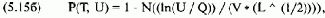
где U = рассматриваемая цена;
Q = текущая цена базового инструмента;
V= годовая волатильность базового инструмента;
Е=доля года, выраженная десятичной дробью, прошедшая с тех пор, когда опцион был приобретен;
N() = функция нормального распределения (уравнение (3.21));
ln() = функция натурального логарифма.
В итоге мы получим взвешенное по вероятности HPR для каждого исхода.
Возможен широкий диапазон результатов, но, к сожалению, эти результаты не непрерывны. Например, время до истечения срока не задается непрерывной функцией. До истечения срока всегда остается целое число; то же верно и для цены базового инструмента. Если цена акции равна, например, 35, а минимальное изменение цены равно 1/8, то между 30 и 40 находится 81 возможное значение.
Зная время, через которое мы собираемся продать опцион, можно рассчитать взвешенные по вероятности HPR для всех возможных цен на этот рыночный день.
В нормальном распределении вероятности 99,73% всех результатов попадают в интервал трех стандартных отклонений от среднего, которое в нашем случае является текущей ценой базового инструмента. Поэтому нам необходимо рассчитать HPR для определенного рыночного дня и каждой дискретной цены между - 3 и + 3 стандартными отклонениями. Можно использовать 4, 5, 6 или больше стандартных отклонений, но ответ от этого не станет значительно точнее. Не следует также сокращать ценовое окно до 2 или 1 стандартного отклонения. Выбор 3 стандартных отклонений, конечно, не является твердым правилом, но в большинстве случаев оно приемлемо. Если мы используем модель Блэка-Шоулса или модель опционов на фьючерсы Блэка, то можно узнать, какому изменению цены базового инструмента U соответствует 1 стандартное отклонение:
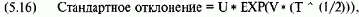
где U = текущая цена базового инструмента;
V = годовая волатильность базового инструмента;
Т = доля года, выраженная десятичной дробью, прошедшая с тех пор. Когда опцион был приобретен;
ЕХР() = экспоненциальная функция.
Отметьте, что стандартное отклонение является функцией времени, прошедшего с момента открытия позиции.
Для точки, которая на Х стандартных отклонений выше текущей цены базового инструмента, получаем:
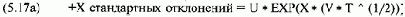
Для точки, которая на Х стандартных отклонений ниже текущей цены базового инструмента, получаем:
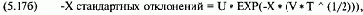
где U =текущая цена базового инструмента;
V =годовая волатильность базового инструмента;
Т =доля года, выраженная десятичной дробью, прошедшая с тех пор, когда опцион был приобретен;
EXPQ = экспоненциальная функция;
Х =число стандартных отклонений от среднего, для которых вы хотите определить вероятности.
Далее следует описание процедуры поиска оптимального f для данного опциона.
Шаг 1. Решите, закроете ли вы позицию по опциону в какой-то конкретный день.
Если нет, тогда в дальнейших расчетах используйте дату истечения срока опциона.
Шаг 2. Определите, сколько дней вы будете удерживать позицию. Затем преобразуйте это число дней в долю года, выраженную десятичной дробью.
Шаг 3. Для дня из шага 1 рассчитайте точки, которые находятся между +3 и -3 стандартными отклонениями.
Шаг 4. Преобразуйте диапазоны цен из шага 3 в дискретные значения. Другими словами, используя приращения по 1 тику, определите все возможные цены диапазона, включая крайние значения.
Шаг 5. Для каждого из полученных результатов рассчитайте Z(T, U - Y) и Р(Т, U), то есть рассчитайте теоретическую цену опциона, а также вероятность того, что базовый инструмент к рассматриваемым датам будет равен определенной цене.
Шаг 6. После того, как вы выполните шаг 5, у вас будут все входные данные, необходимые для расчета взвешенного по вероятности HPR.
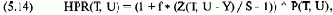
где f = тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т. Эту цену можно определить с помощью любой модели ценообразования, которую пользователь посчитает подходящей;
Р(Т, U) = 1-хвостая вероятность того, что цена базового инструмента равна U, когда время, оставшееся до истечения срока исполнения, равно Т. Это значение можно определить из любой формы распределения, которую пользователь посчитает подходящей;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Необходимо отметить, что форма распределения, используемого для Р(Т, U), не обязательно должна быть такой же, как и в модели ценообразования, применяемой для определения значений Z(T, U - Y). Например, вы используете модель фондовых опционов Блэка-Шоулса для определения значений Z(T, U - Y). Эта модель предполагает логарифмически нормальное распределение изменений цены, однако для определения соответствующего Р(Т, U) вы можете использовать другую форму распределения.
Шаг 7. Теперь мы можем начать поиск оптимального f с помощью метода итераций, перебирая все возможные значения f между 0 и 1, или с помощью метода параболической интерполяции, или любого другого одномерного алгоритма поиска. Подставляя тестируемые значения f в HPR (у вас уже есть HPR для каждого из возможных приращений цены между + 3 и - 3 стандартными отклонениями на дату истечения срока или указанную дату выхода), вы можете найти среднее геометрическое для данного тестируемого значения f. Для этого надо перемножить все HPR, и полученное произведение возвести в степень единицы, деленной на сумма вероятностей:

где G(f, T) = среднее геометрическое HPR для данного тестируемого значения f;
f = тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т. Эту цену можно определить с помощью любой модели ценообразования, которую пользователь посчитает подходящей;
Р(Т, U) = вероятность того, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполнения, равно Т. Это значение можно определить из любой формы распределения, которую пользователь посчитает подходящей;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Значение f, которое в результате даст наибольшее среднее геометрическое, является оптимальным.
Мы можем оптимизировать f, определив оптимальную дату выхода. Другими словами, мы можем найти значение оптимального f для данного опциона на каждый день между текущим днем и днем истечения. Запишем оптимальные f и средние геометрические для каждой указанной даты выхода. Когда мы завершим эту процедуру, мы сможем найти ту дату выхода, которая даст наивысшее среднее геометрическое. Таким образом, мы получим день, когда должны выйти из позиции по опциону для того, чтобы математическое ожидание было наивысшим (т.е. среднее геометрическое было наивысшим). Мы также узнаем, какое оптимальное количество контрактов следует купить.
Теперь у нас есть математический метод, с помощью которого можно выходить из позиции по опциону и покупать опцион при положительном математическом ожидании. Если мы выйдем из позиции в день, когда среднее геометрическое максимально и оно больше 1,0, то следует покупать число контрактов, исходя из оптимального f, которое соответствует наивысшему среднему геометрическому.
Математическое ожидание, о котором мы говорим, — это геометрическое ожидание. Другими словами, среднее геометрическое (минус 1,0) является математическим ожиданием, когда вы реинвестируете прибыли (арифметическое положительное математическое ожидание будет, конечно же, выше, чем геометрическое).
После того как вы найдете оптимальное f для данного опциона, можно преобразовать полученное значение в число контрактов, которое следует покупать:
(5.19) K=INT(E/(S/f)),
где К = оптимальное число опционных контрактов для покупки;
f= значение оптимального Г(от 0 до 1);
S = текущая цена опциона;
Е = общий баланс счета;
1NT() = функция целой части.
Для расчета TWR следует знать, сколько раз мы хотели бы воспроизвести эту же сделку в будущем. Другими словами, если наше среднее геометрическое составляет 1,001 и необходимо найти TWR, которое соответствует этой же игре 100 раз подряд, то TWR будет 1,001^100 = 1,105115698. Поэтому можно ожидать заработка в 10,5115698%, если провести эту сделку 100 раз. Формула для преобразования среднего геометрического в TWR задается уравнением (4.18):
(4.18) TWR = Среднее геометрическое ^ X,
где TWR = относительный конечный капитал;
Х = число раз, которое мы «повторяем» эту игру.
Мы можем определить и другие побочные продукты, например, геометрическое математическое ожидание (среднее геометрическое минус 1). Если мы возьмем наибольший возможный проигрыш (стоимость самого опциона), разделим его на оптимальное f и умножим на геометрическое математическое ожидание, то получим среднюю геометрическую сделку. Как вы уже заметили, при использовании метода оптимального f в торговле опционами появляется еще один побочный продукт — оптимальная дата выхода. Мы рассматривали позиции по опционам при отсутствии направленного движения цены базового инструмента. Для указанной даты выхода точки, смещенные на 3 стандартных отклонения выше и ниже, рассчитываются из текущей цены, таким образом, мы ничего не знаем о будущем направлении цены базового инструмента. В соответствии с математическими моделями ценообразования мы не получим положительное арифметическое математическое ожидание, если будем удерживать позицию по опциону до срока истечения. Однако, как мы уже видели, можно достичь положительного геометрического математического ожидания, если закрыть позицию в определенный день до срока истечения.
Если вы предполагаете определенное изменение цены базового инструмента, его можно учесть. Допустим, мы рассматриваем опционы на базовый инструмент, который в настоящее время стоит 100. Далее предположим, что на основе анализа рынка выявлен тренд, который предполагает цену 105 к дате истечения, и эта дата отстоит на 40 рыночных дней от сегодняшней даты. Мы ожидаем, что цена повысится на 5 пунктов за 40 дней. Если исходить из линейного изменения цены, то цена должна расти в среднем на 0,125 пунктов в день. Поэтому для завтрашнего дня (как дня выхода) мы возьмем значение U, равное 100,125. Для следующей даты выхода возьмем U, равное 100,25. К тому времени, когда указанная дата выхода станет датой истечения срока опциона, U будет равно 105. Если базовым инструментом является акция, то вы должны вычесть дивиденды из U, воспользовавшись уравнением (5.04). Тренд можно учитывать, если изменять каждый день значение U, исходя из сделанного прогноза. Так как уравнения (5.17а) и (5.176) изменятся, значения U повлияют на оптимальные f и побочные продукты. Отметьте, что в уравнениях (5.17а) и (5.176) используются новые значения U, т.е. происходит автоматическое приведение данных, следовательно, полученные оптимальные f будут основаны на данных, приведенных к текущей цене.
Когда вы будете использовать вышеописанную технику работы с оптимальным f, то заметите, что его значение каждый день меняется. Предположим, сегодня вы купили опцион и рассчитали оптимальную дату выхода. Послезавтра цена опциона может измениться, и если вы опять проведете процедуру расчета оптимального f, то также можете получить положительное математическое ожидание, но уже, другую дату выхода. Что это означает?
Ситуация аналогична лошадиным бегам, где можно делать ставки после начала скачки и до их завершения. Шансы постоянно меняются, и вы в любой момент можете обменять купленный билет на деньги. Скажем, до начала скачек вы ставите 2 доллара на определенную лошадь, основываясь на положительном математическом ожидании, и лошадь после первого крута прибегает предпоследней. Предположим, ваш билет, купленный за 2 доллара, стоит теперь только 1,50 доллара.
Вы по-прежнему считаете, что математическое ожидание в пользу вашей лошади, исходя из результатов прошлых скачек и нынешних шансов. Вы решаете, что текущая цена билета в 1,50 доллара на 10% занижена. Можно получить деньги по билету, купленному до начала скачек за 2 доллара (сейчас он стоит 1,50 доллара), и можно также купить билет за 1,50 доллара, чтобы сделать еще одну ставку.
Таким образом, вы получаете положительное математическое ожидание, но на основе билета за 1,50 доллара, а не за 2 доллара. Та же аналогия применима и к опционам, позиция по которым в настоящий момент немного убыточна, но имеет положительное математическое ожидание на основе новой цены. Вы должны использовать другое оптимальное f для новой цены, регулируя текущую позицию (если это необходимо), и закрывать ее, исходя из новой оптимальной даты выхода.
Таким образом, вы используете последнюю ценовую информацию о базовом инструменте, что иногда может заставить вас удерживать позицию до истечения срока опциона. Возможность получения положительного математического ожидания при работе с опционами, которые теоретически справедливо оценены, сначала может показаться парадоксом или просто шарлатанством. Мы знаем, что теоретические цены опционов, найденные с помощью моделей, не позволяют получить положительное математическое ожидание (арифметическое) ни покупателю, ни продавцу. Модели теоретически справедливы с поправкой «если удерживаются до истечения срока». Именно эта отсутствующая поправка позволяет опциону быть справедливо оцененным согласно моделям и все-таки иметь положительное ожидание. Помните, что цена опциона уменьшается со скоростью квадратного корня времени, оставшегося до истечения срока. Таким образом, после первого дня покупки опциона его премия должна упасть в меньшей степени, чем в последующие дни. Рассмотрим уравнения (5.17а) и (5.176) для цен, соответствующих смещению на 4- Х и - Х стандартных величин по истечении времени Т. Окно цен каждый день расширяется, но все медленнее и медленнее, в первый день скорость расширения максимальна. Таким образом, в первый день падение премии по опциону будет минимальным, а окно Х стандартных отклонений будет расширяться быстрее всего. Чем меньше времени пройдет, тем с большей вероятностью мы будем иметь положительное ожидание по длинной позиции опциона, и чем шире окно Х стандартных отклонений, тем вероятнее, что мы будем иметь положительное ожидание, так как убыток ограничен ценой опциона, а возможная прибыль не ограничена. Между окном Х стандартных отклонений, которое с каждым днем становится все шире и шире (хотя со все более медленной скоростью), и премией опциона (падение которой с каждым днем происходит все быстрее и быстрее) происходит «перетягивание каната».
В первый день математическое ожидание максимально, хотя оно может и не быть положительным. Другими словами, математическое ожидание (арифметическое и геометрическое) самое большое после того, как вы продержали опцион 1 день (оно в действительности самое большое в тот момент, когда вы приобретаете опцион, и далее постепенно понижается, но мы рассматриваем дискретные величины).
Каждый последующий день ожидание понижается, но все медленнее и медленнее.
Следующая таблица иллюстрирует понижение ожидания по длинной позиции опциона. Этот пример уже упоминался в данной главе. Колл-опцион имеет цену исполнения 100, базовый инструмент стоит также 100; дата истечения — 911220.
Волатильность составляет 20%, а сегодняшняя дата 911104. Мы используем формулу товарных опционов Блэка (Н определяется из уравнения (5.07), R = 5%) и 260,8875-дневный год. Возьмем 8 стандартных отклонений для расчета оптимального f, а минимальный шаг тика примем равным 0,1.

Значения столбца «AHPR» являются средними арифметическими HPR (расчет будет рассмотрен позднее в этой главе), a GHPR является средним геометрическим HPR. Столбец «f» представляет оптимальные f, из которых находятся значения столбцов AHPR и GHPR. Арифметическое математическое ожидание равно AHPR - 1, а геометрическое математическое ожидание равно GHPR - 1. Отметьте, что наибольшие математические ожидания (необязательно положительные ожидания, как в этом примере) возникают в день после приобретения опциона. Каждый последующий день ожидания уменьшаются, причем скорость уменьшения с течением времени замедляется. После 911106 математические ожидания (HPR - 1) становятся отрицательными. ' Если бы нам пришлось торговать по этой информации, мы могли бы войти сегодня (911104) и выйти при закрытии завтра (911105). Справедливая цена опциона равна 2,861. Если мы допустим, что он котируется по цене 100 долларов за полный пункт, цена опциона составит 2,861 * $100 ^ $286,10. Разделив эту цену на оптимальное f= 0,0806, мы найдем, что следует торговать одним опционом на каждые 3549,63 доллара на балансе счета.
Если бы мы держали опцион до закрытия 911106 (последний день), когда он все еще имеет положительное математическое ожидание, то открыв позицию сегодня, используя для дня выхода (911106) соответствующее оптимальное f= 0,0016, торговали бы 1 контрактом на каждые 178 812,50 доллара на балансе счета ($286,10 / 0,0016). Отметьте, что при этом ожидание намного ниже, чем в случае торговли 1 контрактом на каждые 3549,63 доллара на балансе счета и выхода по цене закрытия завтра (911105).
Скорость изменения между двумя функциями: уменьшением премии с течением времени и расширением окна Х стандартных отклонений, может создать положительное математическое ожидание для длинной позиции по опциону. Это ожидание имеет наибольшее значение в момент открытия позиции и после этого понижается с уменьшающейся скоростью. Таким образом, справедливо оцененный опцион (на основе вышеизложенных моделей) может иметь положительное математическое ожидание, если позицию по нему закрыть в начале периода падения премии. В следующей таблице рассматривается тот же колл-опцион с ценой исполнения 100, но на этот раз используются окна различного размера (различные значения стандартных отклонений):

AHPR и GHPR — это арифметические и геометрические HPR при оптимальном f для дня закрытия 911105 (самая благоприятная дата выхода, так как она имеет наивысшие AHPR и GHPR). f соответствует оптимальному f для 911105. Значения строки «Дата выхода» — это последние даты, когда еще существует положительное ожидание (т.е. когда AHPR и GHPR больше 1). Интересно отметить, что AHPR, GHPR, f и Дата выхода сходятся к определенным значениям, когда мы увеличиваем число стандартных отклонений. За пределами 5 стандартных отклонений эти значения едва заметно изменяются, за пределами 8 стандартных отклонений они практически вообще не изменяются. Недостатком использования большого числа стандартных отклонений является необходимость в значительном компьютерном времени. В нашем примере это не так важно, но когда мы будем рассматривать одновременную торговлю по нескольким позициям, вы увидите, что каждая дополнительная позиция экспоненциально увеличивает необходимое компьютерное время. Для одной позиции 8 стандартных отклонений более чем достаточно, однако для нескольких позиций, открытых одновременно, необходимо уменьшить число стандартных отклонений. Следует отметить, что правило 8 стандартных отклонений применимо только тогда, когда логарифмы изменений цены распределены нормально.
Содержание раздела