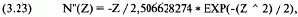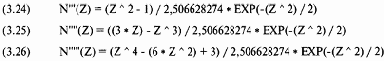Иногда требуется знать вторую производную функции N(Z). Так как функция N(Z) дает нам значение площади под кривой при Z, а функция N'(Z) дает нам высоту самой кривой при значении Z, тогда функция N"(Z) дает нам мгновенный наклон (instantaneous slope) кривой при данном значении Z:



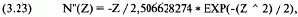
где ЕХР() = экспоненциальная функция.
Найдем наклон кривой N'(Z) при +2 стандартных отклонениях:

N"(Z) = -2 I 2,506628274 * ЕХР(-(+2^ 2) / 2) = -2 / 2,506628274 * ЕХР(-2) = -2 /

h1>
Теперь мы знаем, что мгновенная скорость изменения функции N'(Z) при Z = +2 равна-0,1079968336. Это означает повышение/понижение за период, поэтому, когда Z = +2, кривая N'(Z) повышается на -0,1079968336. Эта ситуация показана на рисунке 3-13.
Последующие производные даются далее для справки. Они не будут использоваться в оставшейся части книги и представлены для полноты освещения темы:



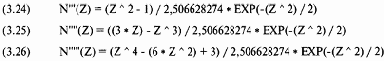
В качестве последнего дополнения к сказанному о нормальном распределении стоит заметить, что на самом деле это распределение не такое остроконечное, как на графиках, представленных в данной главе. Реальная форма нормального распределения показана на рисунке 3-14. Отметьте, что здесь масштабы двух осей одинаковы, в то время как в других графических примерах они отличаются для придания более вытянутой формы.

Содержание раздела

---