Время, необходимое для достижения определенной цели, и проблема дробного f
Допустим, мы знаем среднее арифметическое HPR и среднее геометрическое HPR для данной системы. Мы можем определить стандартное отклонение HPR из формулы для расчета оценочного среднего геометрического: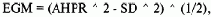
где AHPR = среднее арифметическое HPR;
SD = стандартное отклонение значений HPR.
Поэтому мы можем рассчитать стандартное отклонение SD следующим образом:
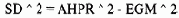
Возвращаясь к нашей игре с броском монеты 2:1, где математическое ожидание 0,50 долларов и оптимальное f- ставка в 1 доллар на каждые 4 доллара на счете, мы получим среднее геометрическое 1,06066. Для определения среднего арифметического HPR можно использовать уравнение (2.05):
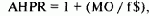
где AHPR = среднее арифметическое HPR;
МО = арифметическое математическое ожидание в единицах;
f$= наибольший проигрыш/-f
f = оптимальное f (от 0 до 1).
Таким образом, среднее арифметическое HPR равно:
AHPR =1+(0,5/(-1/-0,25)) =1+(0,5/4) =1+0,125 =1,125
Теперь, так как у нас есть AHPR и EGM, мы можем использовать уравнение (2.04) для определения оценочного стандартного отклонения HPR:

Таким образом, SD ^ 2, то есть дисперсия HPR, равна 0,140625364. Извлекая квадратный корень из этой суммы, мы получаем стандартное отклонение HPR =0,140625364 ^(1/2) =0,3750004853. Следует отметить, что это оценочное стандартное отклонение, так как при его расчете используется оценочное среднее геометрическое.
Это не совсем точный расчет, но вполне приемлемый для наших целей. Предположим, мы хотим преобразовать значения для стандартного отклонения (или дисперсии), арифметического и среднего геометрического HPR, чтобы отражать торговлю не оптимальным f, а некоторой его частью. Эти преобразования даны далее:

где FRAC = используемая дробная часть оптимального f;
АН PR= среднее арифметическое HPR при оптимальном f;
SD = стандартное отклонение HPR при оптимальном f;
FAHPR== среднее арифметическое HPR при дробном f;
FSD = стандартное отклонение HPR при дробном f;
FGHPR = среднее геометрическое HPR при дробном f.
Например, мы хотим посмотреть, какие значения приняли бы FAHPR, FGHPR и FSD в игре с броском монеты 2:1 при половине оптимального f (FRAC = 0,5). Мы знаем, что AHPR= 1,125 и SD = 0,3750004853. Таким образом:

Для оптимального f= 0,25 (1 ставка на каждые 4 доллара на счете) мы получаем значения 1,125, 1,06066 и 0,3750004853 для среднего арифметического, среднего геометрического и стандартного отклонения HPR соответственно. При дробном (0,5) f =0,125 (1 ставка на каждые 8 долларов на счете) мы получаем значения 1,0625, 1,04582499 и 0,1875002427 для среднего арифметического, среднего геометрического и стандартного отклонения HPR соответственно. Посмотрим, что происходит, когда мы используем стратегию дробного f. Мы уже знаем, что при дробном f заработаем меньше, чем при оптимальном f. Более того, мы определили, что проигрыши и дисперсии прибылей будут меньше при дробном f. Что произойдет со временем, необходимым для достижения определенной цели?
Мы можем определить только ожидаемое количество сделок, необходимое для достижения определенной цели. Это не то же самое, что ожидаемое время, требуемое для достижения определенной цели, но, так как наши измерения производятся в сделках, мы будем считать время и количество сделок синонимами.
(2.09) N = 1п(Цель) / 1n(Среднее геометрическое),
где N = ожидаемое количество сделок для достижения цели;
Цель = цель в виде множителя первоначального счета, т.е. TWR;
1n() = функция натурального логарифма.
Вернемся к нашему примеру с броском монеты 2:1. При оптимальном f среднее геометрическое равно 1,06066, а при половине f оно составляет 1,04582499. Теперь давайте рассчитаем ожидаемое количество сделок, необходимое для удвоения нашего счета (Цель = 2). При полном f:
N=ln(2)/ln( 1,06066) =0,6931471/0,05889134 =11,76993
Таким образом, в игре с броском монеты 2:1 при полном f следует ожидать 11,76993 сделок для удвоения нашего счета. При половине f получаем:
N=ln(2)/ln( 1,04582499) =0,6931471/0,04480602 = 15,46996
Таким образом, при половине f мы ожидаем, что потребуется 15,46996 сделок для удвоения счета. Другими словами, чтобы достичь цели при торговле на уровне f/ /2, от нас понадобится на 31,44% сделок больше. Ну что же, это звучит не так уж плохо. Проявляя терпение для достижения поставленной цели, мы потратим времени на 31,44% больше, но сократим худший проигрыш и дисперсию наполовину. Согласитесь, половина — это довольно много. Чем меньшую часть оптимального f вы будете использовать, тем более гладкую кривую счета получите, и тем меньшее время вы будете в проигрыше. Теперь посмотрим на эту ситуацию с другой стороны. Допустим, вы открываете два счета: один для торговли с полным f и один для торговли с половиной f. После 12 игр ваш счет с полным f увеличится в 2,02728259 в 12 раза. После 12 сделок (с половиной f) он вырастет в 1,712017427 (1,04582499 ^ 12) раза. С половиной f первоначальный счет увеличится в 2,048067384 (1,04582499 ^ 16) раза при 16 сделках. Поэтому, торгуя на одну треть дольше, вы достигнете той же цели, что и при полном оптимальном f, но при активности, меньшей наполовину. Однако к 16 сделке счет с полным f будет в 2,565777865 (1,06066 ^ 16) раза больше вашего первоначального счета. Полное f продолжает увеличивать счет. К 100 сделке ваш счет с половиной f увеличится в 88,28796546 раз, но полное f увеличит его в 361,093016 раз!
Единственный минус торговли с дробным f— это большее время, необходимое для достижения определенной цели. Все дело во времени. Мы можем вложить деньги в казначейские обязательства и достичь-таки заданной цели через определенное время с минимальными промежуточными падениями баланса и дисперсией! Время — это суть проблемы.
Содержание раздела
