Рассматривайте каждую игру как бесконечно повторяющуюся
Следующая аксиома, касающаяся торговли фиксированной долей, относится к максимизации текущего события, как будто оно должно быть осуществлено бесконечное количество раз в будущем. Мы определили, что для процесса независимых испытаний вы должны всегда использовать оптимальное и постоянное f, но при наличии зависимости оптимальное f уже не будет постоянной величиной.
Допустим, в нашей системе существует зависимость, в соответствии с которой подобное порождает подобное, а доверительная граница достаточно высока. Для наглядности мы будем использовать уже знакомую нам игру 2:1. Система показывает, что если последняя игра выигрышная, то следующая игра имеет 55% шанс выигрыша. Если последняя игра проигрышная, то следующая игра имеет 45% шанс проигрыша.
Таким образом, если последняя игра была выигрышная, то исходя из формулы Келли, уравнение (1.10) для поиска оптимального f (так как результаты игры имеют бернуллиево распределение), получим:
(1.10) f =((2+1)* 0,55-1)/2 =(3*0,55- 1)/2=0,65/2=0,325
После проигрышной игры наше оптимальное f равно:
f =((2+1)* 0,45-1)/2 =(3*0,45-1) /2 =0,35/2 =0,175
Разделив наибольший проигрыш системы (т.е. -1) на отрицательные оптимальные f, мы получим 1 ставку на каждые 3,076923077 единицы на счете после выигрыша и 1 ставку на каждые 5,714285714 единицы на счете после проигрыша. Таким образом мы максимизируем рост в долгосрочной перспективе.
Отметьте, что в этом примере ставки как после выигрышей, так и после проигрышей все еще имеют положительное математическое ожидание. Что произойдет, если после проигрыша вероятность выигрыша будет равна 0,3? В таком случае математическое ожидание имеет отрицательное значение и оптимального f не существует, таким образом, вам не следует использовать эту игру:
(1.03) М0=(0,3*2)+(0,7*-1) =0,6-0,7 =-0,1
В этом случае следует использовать оптимальное количество только после выигрыша и не торговать после проигрыша. Если зависимость действительно существует, вы должны изолировать сделки рыночной системы, основанные на зависимости, и обращаться с изолированными сделками как с отдельными рыночными системами. Принцип, состоящий в том, что асимптотический рост максимизируется, когда каждая игра осуществляется бесконечное количество раз в будущем, также применим к нескольким одновременным играм (или торговле портфелем).
Рассмотрим две системы ставок, А и Б. Обе имеют отношение выигрыша к проигрышу 2:1, и обе выигрывают 50% времени. Допустим, что коэффициент корреляции между двумя системами равен 0. Оптимальные f для обеих систем (при раздельной, а не одновременной торговле) составляют 0,25 (т.е. одна ставка на каждые 4 единицы на балансе). Оптимальные f при одновременной торговле в обеих системах составляют 0,23 (т.е. 1 ставка на каждые 4,347826087 единицы на балансе счета). В случае, когда система Б торгует только две трети времени, некоторые трейдеры разорятся, если обе системы не будут торговать одновременно.
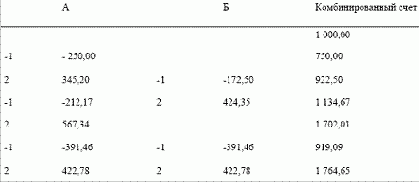
Первая последовательность показана при начальном комбинированном счете в 1000 единиц, и для каждой системы оптимальное f соответствует 1 ставке на каждые 4,347826087 единицы:

Рассмотрим теперь ситуацию, когда А торгует отдельно от Б. В этом случае мы делаем 1 ставку на каждые 4 единицы на комбинированном счете для системы А (так как это оптимальное f для одной игры). В игре с одновременными ставками мы все равно ставим 1 единицу на каждые 4,347826087 единицы на балансе счета как для А, так и для Б.
Отметьте, что независимо от того, отдельная это ставка или одновременная ставка по А и Б, мы применяем то оптимальное f, которое увеличивает доход при бесконечном повторении ставок.
Как видите, с помощью этого метода мы получаем небольшой выигрыш, и чем больше сделок проходит, тем больше этот выигрыш. Тот же принцип применяется к торговле портфелем, где не все компоненты портфеля находятся на рынке в определенный момент времени. Вам следует торговать на оптимальных уровнях для комбинации компонентов (или одного компонента), чтобы получить в итоге оптимальный рост, как будто этой комбинацией компонентов (или одним компонентом) придется торговать бесконечное количество раз в будущем.
Содержание раздела


