Порог геометрической торговли

Существует еще один хороший подход для трейдеров, которые только начинают торговать, правда, если вы не используете только что упомянутый метод. При таком подходе используется еще один побочный продукт оптимального f — порог геометрической торговли. Мы уже знаем такие побочные продукты оптимального f, как TWR, среднее геометрическое и т.д.; они были получены из оптимального f и дают нам информацию о системе. Порог геометрической торговли — это еще один из таких побочных расчетов. По существу, порог геометрической торговли говорит нам, в какой точке следует переключиться на торговлю фиксированной долей, предполагая, что мы начинаем торговать фиксированным количеством контрактов. Вспомните пример с броском монеты, где мы выигрываем 2 доллара, если монета падает на лицевую сторону, и проигрываем 1 доллар, если она падает на обратную сторону. Мы знаем, что оптимальное f= 0,25, т.е. 1 ставка на каждые 4 доллара баланса счета. Если мы торгуем на основе постоянного количества контрактов, то в среднем выигрываем 0,50 долларов за игру. Однако если мы начнем торговать фиксированной долей счета, то можем ожидать выигрыша в 0,2428 доллара на единицу за одну игру (при геометрической средней торговле).
Допустим, мы начинаем с первоначального счета в 4 доллара и поэтому делаем 1 ставку за одну игру. В конце концов, когда счет увеличивается до 8 долларов, следует делать 2 ставки за одну игру. Однако 2 ставки, умноженные на геометрическую среднюю торговлю 0,2428 доллара, дадут в итоге 0,4856 доллара.
Не лучше ли придерживаться 1 ставки при уровне баланса 8 долларов, так как нашим ожиданием за одну игру все еще будет 0,50 доллара? Ответ — «да».
Причина в том, что оптимальное f рассчитывается на основе контрактов, которые бесконечно делимы, чего в реальной торговле не бывает.

Мы можем найти точку, где следует перейти к торговле двумя контрактами, основываясь на формуле порога геометрической торговли Т:
Т = ААТ / GAT * Наибольший убыток / -f,
где Т = порог геометрической торговли;
ААТ = средняя арифметическая сделка;
GAT = средняя геометрическая сделка;
f= оптимальное f (от 0 до 1). Для нашего примера с броском монеты (2 к I):

Т=0,50 / 0,2428*-1 / -0,25 =8,24

Поэтому следует переходить на торговлю двумя контрактами, когда счет увеличится до 8,24 доллара, а не до 8,00 долларов. Рисунок 2-1 иллюстрирует порог геометрической торговли для игры с 50% шансов выигрыша 2 долларов и 50% шансов проигрыша 1 доллара. Отметьте, что дно кривой порога геометрической торговли соответствует оптимальному f. Порог геометрической торговли является оптимальным уровнем баланса для перехода от торговли одной единицей к торговле двумя единицами. Поэтому если вы используете оптимальное f, то сможете перейти к геометрической торговле при минимальном уровне баланса счета. Теперь возникает вопрос: «Можем ли мы использовать подобный подход, чтобы узнать, когда переходить от 2 к 3 контрактам?», а также: «Почему в самом начале размер единицы не может быть 100 контрактов, если вы начинаете с достаточно большого счета, а не такого, который позволяет торговать лишь одним контрактом?» Разумеется, можно использовать этот метод при работе с размером единицы, большим 1. Однако это корректно в том случае, если вы не уменьшите размер единицы до перехода к геометрическому способу торговли. Дело в том, что до того, как вы перейдете на геометрическую торговлю, вы должны будете торговать постоянным размером единицы.

Допустим, вы начинаете со счета в 400 единиц в игре с броском монеты 2 к 1. Оптимальное f в долларах предполагает торговлю 1 контрактом (1 ставка) на каждые 4 доллара на счете. Поэтому начинайте торговать 100 контрактами (сделав 100 ставок) в первой сделке. Ваш порог геометрической торговли равен 8,24 доллара, и поэтому следует торговать 101 контрактом на уровне баланса 404,24 доллара. Вы можете преобразовать порог геометрической торговли, который соответствует переходу с 1 контракта к 2 следующим образом:

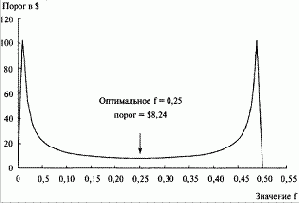
Рисунок 2-1 Порог геометрической торговли для броска монеты 2 к 1

Преобразованное Т = EQ + Т - (Наибольший проигрыш / -f), где EQ = начальный уровень баланса счета;
Т = порог геометрической торговли для перехода с одного контракта к двум;
f= оптимальное f (от 0 до 1).
Преобразованное Т = 400 + 8,24 - (-1 / -0,25) = 400 + 8,24 - 4 = 404,24

Таким образом, вы перейдете к торговле 101 контрактом (101 ставке), только когда баланс счета достигнет 404,24 доллара. Допустим, вы торгуете постоянным количеством контрактов, пока баланс счета не достигнет 404,24 доллара, где вы начнете применять геометрический подход. Пока баланс счета не достигнет 404,24 доллара, вы будете торговать 100 контрактами в последующих сделках независимо от суммы счета. Если после того, как вы пересечете порог геометрической торговли (то есть после того, как баланс счета достигнет 404,24 доллара), вы понесете убыток и баланс упадет ниже 404,24 доллара, вы вернетесь снова к торговле на основе 100 контрактов и будете так торговать до тех пор, пока снова не пересечете геометрический порог. Невозможность уменьшения количества контрактов при уменьшении счета, когда вы находитесь ниже геометрического порога, является недостатком при использовании этой процедуры, когда контрактов больше 2. Если вы торгуете только 1 контрактом, геометрический порог является реальным методом для определения того, на каком уровне баланса начать торговать 2 контрактами (так как вы не можете торговать менее чем 1 контрактом при понижении баланса). Однако этот метод не работает, когда речь идет о переходе от 2 контрактов к 3, так как метод базируется на том, что вы начинаете торговлю с постоянного количества контрактов. То есть, если вы торгуете 2 контрактами, метод не будет работать (за исключением случая, когда вы откажетесь от возможности понизить количество контрактов до одного при падении уровня баланса). Таким образом, начиная торговлю со 100 контрактов, вы не можете перейти к торговле меньшим числом контрактов. Если вы не будете уменьшать количество контрактов, которыми в настоящее время торгуете, при понижении баланса, то порог геометрической торговли или его преобразованная версия из уравнения (2.03) будет уровнем баланса, достаточным для добавления следующего контракта. Проблема этой операции (не уменьшать при понижении) состоит в том, что вы заработаете меньше (TWR будет меньше) в асимптотическом смысле. Вы не выиграете столько, сколько бы выиграли при торговле полным оптимальным f. Более того, ваши проигрыши будут больше, и риск банкротства увеличится. Поэтому порог геометрической торговли будет эффективен, если вы начнете с наименьшего размера ставки (1 контракт) и повысите его до 2. Оптимально, если средняя арифметическая сделка более чем в два раза превышает среднюю геометрическую сделку. Предложенный метод следует использовать, когда вы не можете торговать дробными единицами.

Содержание раздела