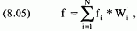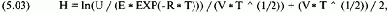Страхование портфеля — четвертый метод переразмещения

Предположим, вы управляете фондом акций. Рисунок 8-2 демонстрирует типичную стратегию страхования портфеля, также известную как динамическое хеджирование. Пусть текущая стоимость портфеля равна 100 долларам за акцию. Стандартный портфель, он изображен прямой линией, в точности следует за рынком акций. Застрахованный портфель изображен пунктирной линией. Отметьте, что пунктирная линия проходит ниже прямой линии, когда портфель находится на уровне или выше своей первоначальной стоимости (100). Величина, на которую пунктирная линия ниже прямой линии, отражает стоимость страхования портфеля.
Когда стоимость портфеля уменьшается, страхование портфеля ограничивает падение на некотором уровне (в данном случае 100) за вычетом расходов на осуществление стратегии.
Страхование портфеля соответствует покупке пут-опциона по портфелю.
Допустим, фонд, которым вы управляете, состоит только из 1 акции стоимостью 100 долларов. Покупка пут-опциона на эту акцию с ценой исполнения 100 долларов при цене опциона 10 долларов соответствует пунктирной линии на рисунке 8-2. Худшее, что может произойти в данном случае с портфелем (1 акция и 1 пут-опцион), состоит в том, что по истечении опциона вы продадите акцию за 100 долларов, но потеряете 10 долларов (стоимость этого опциона). Таким образом, минимальная стоимость портфеля будет 90 долларов, независимо от того, насколько упадет базовая акция. При росте вы понесете некоторые убытки из-за того, что стоимость портфеля уменьшится на стоимость опциона.
Если сопоставить рисунок 8-2 с фундаментальным уравнением торговли и оценочным TWR из уравнения (1.19в), становится ясно, что в асимптотическом смысле застрахованный портфель лучше незастрахованного. Другими словами, если вы умны настолько, насколько глупа ваша худшая ошибка, то, застраховав портфель, вы ограничите последствия такой ошибки.
Обратите внимание, что длинная позиция по колл-опциону дает тот же результат, что и длинная позиция по базовому инструменту совместно с длинной позицией по пут-опциону с той же ценой исполнения и датой истечения, что и у колл-опциона. Когда мы говорим о том же результате, имеются в виду эквивалентные соотношения риск/выигрыш разных портфелей. Таким образом, пунктирная линия на рисунке 8-2 может также представлять длинную позицию по колл-опциону с ценой исполнения 100.
Посмотрим, как работает динамическое хеджирование при страховании портфеля. Допустим, вы, как управляющий фондом, приобретаете 100 акций по цене 100 долларов за акцию. Давайте смоделируем колл-опцион по этой акции.
Сначала определим минимальный ценовой уровень рассматриваемой акции.
Например, установим его на 100. Далее определим дату истечения этого гипотетического опциона. Пусть дата истечения будет последним днем текущего квартала.
Теперь рассчитаем дельту колл-опциона при цене исполнения 100 и выбранной дате истечения. Вы можете использовать уравнение (5.05) для поиска дельты фондового колл-опциона (можно использовать дельту для любой модели опционов, мы же будем использовать модель фондовых опционов Блэка-Шоулса). Допустим, дельта равна 0,5, т. е. в данный актив следует инвестировать 50% счета.
Таким образом, вам следует купить только 50 акций, а не 100 акций, которые вы бы купили, если бы не страховали портфель. Если цена акции будет расти, то же будет происходить с дельтой и количеством акций. Верхняя граница дельты равна единице, что соответствует инвестированию 100% средств. Если цена акции будет понижаться, то же будет происходить с дельтой и размером позиции по акциям.
Нижняя граница дельты равна 0 (при этом дельта пут-опциона равна -1), и в этой точке следует полностью закрыть позицию по акциям.

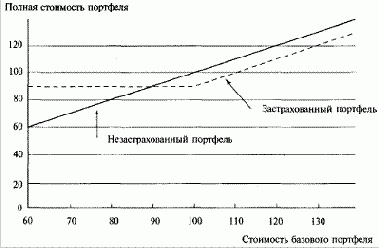
Рисунок 8-2 Страхование портфеля

На практике портфельные менеджеры используют неагрессивные методы динамического хеджирования, что предполагает отсутствие торговли самими ценными бумагами портфеля. Стоимость портфеля зависит от текущей дельты и модели и регулируется с помощью фьючерсов, а иногда пут-опционов. Плюсом использования фьючерсов является низкая стоимость трансакций. Короткая продажа фьючерсов против портфеля эквивалентна продаже части портфеля. При падении портфеля продается больше фьючерсных контрактов, когда же стоимость портфеля растет, эти короткие позиции закрываются. Потери по портфелю, когда приходится закрывать короткие фьючерсные позиции при росте цен на акции, являются издержками по страхованию портфеля и эквивалентны стоимости гипотетических смоделированных опционов. Преимущество динамического хеджирования состоит в том, что оно позволяет с самого начала точно рассчитать издержки. Менеджерам, применяющим такую стратегию, это позволяет сохранить весь портфель ценных бумаг, в то время как размещение активов регулируется посредством фьючерсов и/или опционов. Предложенный неагрессивный метод, основанный на использовании фьючерсов и/или опционов, позволяет разделить размещение активов и активное управление портфелем. При страховании вы должны постоянно регулировать портфель с учетом текущей дельты, т. е. с определенной периодичностью, например, каждый день вы должны вводить в модель ценообразования опционов текущую стоимость портфеля, время до даты истечения, уровень процентной ставки и волатильность портфеля для определения дельты моделируемого пут-опциона. Если к дельте, которая может принимать значения 0 и -1 прибавить единицу, то вы получите соответствующую дельту колл-опциона, которая будет коэффициентом хеджирования, т.е. долей вашего счета, которую следует инвестировать в фонд. Допустим, коэффициент хеджирования в настоящий момент составляет 0,46. Размер фонда, которым вы управляете, эквивалентен 50 фьючерсным контрактам S&P. Так как вы хотите инвестировать только 46% средств, вам надо изъять остальные 54%, т.е. 27 контрактов. Поэтому при текущей стоимости фонда, при данных уровнях процентной ставки и волатильности фонд должен иметь короткие позиции по 27 контрактам S&P одновременно с длинной позицией по акциям. Так как необходимо постоянно перерассчитывать дельту и регулировать портфель, метод называется стратегией динамического хеджирования. Одна из проблем, связанная с использованием фьючерсов, состоит в том, что рынок фьючерсов в точности не следует за рынком спот. Кроме того, портфель. против которого вы продаете фьючерсы, может в точности не следовать за индексом рынка спот, лежащего в основе рынка фьючерсов. Подобные ошибки могут добавляться к расходам по страхованию портфеля. Более того, когда ваш моделируемый опцион подходит очень близко к дате истечения, а стоимость портфеля приближается к цене исполнения, гамма моделируемого опциона астрономически возрастает. Гамма — это мгновенная скорость изменения дельты, т.е. коэффициента хеджирования.

Другими словами, гамма является дельтой дельты. Если дельта изменяется очень быстро (т. е. моделируемый опцион имеет высокую гамму), страхование портфеля становится крайне обременительным. Существует множество путей обхода этой проблемы, и некоторые из них довольно сложны. Один из самых простых способов заключается в том, чтобы совместно использовать фьючерсы и опционы для изменения как дельты, так и гаммы моделируемого опциона. Большое значение гаммы, как правило, создает проблемы только тогда, когда подходит дата истечения, а стоимость портфеля и цена исполнения моделируемого опциона сближаются. Существует интересная связь между оптимальным f и страхованием портфеля. Можно сказать, что при открытии позиции вы инвестируете f процентов средств. Рассмотрим азартную игру, где оптимальное f=0,5, наибольший проигрыш равен -1 и вы располагаете 10 000 долларов. В таком случае следует ставить 1 доллар на каждые 2 доллара на счете, так как, разделив -1 (наибольший проигрыш) на -0,5 (отрицательное оптимальное f), мы получим 2.
Разделив 10000 долларов на 2, мы получим 5000 долларов, поэтому следует ставить 5000 долларов, что соответствует доле f, т.е. 50% ваших денежных средств. Если умножить 10 000 долларов на f= 0,5, мы получим тот же результат, 5000 долларов, т.е. вам следует задействовать f процентов имеющихся денежных средств. Аналогично, если ваш наибольший проигрыш равен 250 долларам, а все остальное остается без изменений, то следует ставить 1 доллар на каждые 500 долларов вашего счета (так как -$250 / -0,5 = $500). Разделив 10 000 долларов на 500 долларов, мы найдем, что ставка равна 20 долларам. Так как максимальный проигрыш по одной ставке составляет 250 долларов, вы, таким образом, рискуете долей счета f, т.е. 50%, или 5000 долларов ($250 * 20). Мы можем сказать, что f равно доле вашего счета, которая подвержена риску, или f равно коэффициенту хеджирования. Так как f применимо только к активной части портфеля, при стратегии динамического дробного f коэффициент хеджирования портфеля равен:

(8.04а) H=f*A/E,

где Н = коэффициент хеджирования портфеля;
f= оптимальное Г(от 0 до 1);
А = активная часть средств счета;
Е = общий баланс счета.

Уравнение (8.04а) дает нам коэффициент хеджирования для портфеля при стратегии динамического дробного f. Страхование портфеля также работает при статическом дробном f, только коэффициент А/Е становится равным единице, а оптимальное f умножается на соответствующий коэффициент. Таким образом, при стратегии статического дробного f коэффициент хеджирования равен:

(8.046) H=f*FRAC,

где Н = коэффициент хеджирования портфеля;
f = оптимальное f (от 0 до 1);
FRAC = используемая доля оптимального f.
Как правило, счет используется для работы в нескольких рыночных системах. В этом случае переменная f в уравнении (8.04а) или (8.046) должна рассчитываться следующим образом:

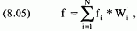
где f = f (от 0 до 1), используемое в уравнении (8.04а) или (8.046);
N = общее число рыночных систем в портфеле;
W. = вес компонента i в портфеле (из единичной матрицы);
f i = фактор f (от 0 до 1) компонента i в портфеле.
Можно сказать, что при торговле на основе динамического дробного f мы проводим страхование портфеля. При этом минимально допустимый уровень стоимости портфеля равен: первоначальный неактивный баланс плюс стоимость проведения страхования. Далее для простоты будем считать, что нижняя граница счета равна первоначальному неактивному балансу.
Обратите внимание, что уравнения (8.04а) и (8.046) позволяют получить дельту моделируемого колл-опциона. Разделение счета на неактивный и активный подсчета (для использования стратегии динамического дробного f) эквивалентно покупке пут-опциона, цена исполнения которого больше текущей стоимости базового актива, а дата истечения наступает не скоро. Мы можем также сказать, что торговля с использованием стратегии динамического дробного f аналогична покупке колл-опциона, цена исполнения которого меньше текущей стоимости базового актива. Данное свойство страхования портфеля справедливо для любой стратегии динамического дробного f, независимо от того, используем мы усреднение по акциям, планирование сценария или полезность инвестора.
Можно использовать страхование портфеля в качестве метода переразмещения.
Сначала следует определить значение минимального ценового уровня, затем для выбранной модели опциона вы должны определить дату истечения, уровень волатильности и другие входные параметры, которые позволят рассчитать дельту.
После того как будет найдена дельта, вы можете определить величину активного баланса. Так как дельта для счета (переменная Н в уравнении (8.04а)) равна дельте моделируемого колл-опциона, мы можем заменить Н в уравнении (8.04а) на D:

D=f*A/E

или

(8.06) D / f= А / Е, если D < f (в противном случае А / Е = 1),

где D = коэффициент хеджирования моделируемого опциона;
f = f (от 0 до 1) из уравнения (8.05);
А = активная часть средств счета;
Е = общий баланс счета.

Так как отношение А/ Е равно доле активного счета, можно сказать, что отношение активного баланса к общему балансу равно отношению дельты колл-опциона к f из уравнения (8.05). Заметьте, если D > f, тогда предполагается, что вы размещаете больше 100% баланса счета в активный баланс. Так как это невозможно, для активного баланса существует верхняя граница — 100%. Вы можете использовать уравнение (5.05) для поиска дельты колл-опциона на акции или уравнение (5.08) для поиска дельты колл-опциона на фьючерсы.
Проблема использования страхования портфеля в качестве метода переразмещения состоит в том, что переразмещение уменьшает эффективность стратегии динамического дробного f, которая асимптотически способна дать большую прибыль, чем стратегия статического дробного f. Таким образом, страхование портфеля как стратегия переразмещения на основе динамического дробного f является не самым лучшим подходом Теперь рассмотрим реальный пример страхования портфеля. Вспомним геометрический оптимальный портфель Toxico, Incubeast и LA Garb, который достигается при V= 0,2457. Преобразуем дисперсию портфеля в значение волатильности для модели ценообразования опционов. Волатильность задается годовым стандартным отклонением. Уравнение (8.07) показывает зависимость между дисперсией портфеля и оценочной волатильностью для опциона по портфелю:

(8.07) OV=V'0.5)ACTVYEARDAYS^0.5,

где OV = волатильность для опциона по портфелю;
V = дисперсия портфеля;
ACTV = текущая активная часть баланса счета;
YEARDAYS = число рыночных дней в году.
Если мы исходим из того, что в году 251 рыночный день и доля активного баланса равна 100% (1,00), то:

OV= (0,2457 ^ 0,5) * 1 * 251 ^ 0,5 = 0,4956813493 * 15,84297952 = 7,853069464

Полученное значение соответствует волатильности свыше 785%! Поскольку речь идет о торговле на уровне оптимального f при 100% активном балансе, значение волатильности настолько велико. Так как мы собираемся использовать страхование портфеля в качестве метода переразмещения, то ACTV= 1,00.
Уравнение (5.05) позволяет рассчитать дельту колл-опциона:
(5.05) Дельта колл-опциона = N(H) Значение Н для (5.05) найдем из уравнения (5.03):

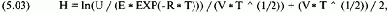
где U = цена базового инструмента;
Е = цена исполнения опциона;
Т = доля года, оставшаяся до истечения срока исполнения, выраженная десятичной дробью;
V = годовая волатильность в процентах;
R = безрисковая ставка;
1n() = функция натурального логарифма;
N() = кумулятивная нормальная функция распределения вероятностей, задаваемая уравнением (3.21).
Отметьте, что мы используем модель ценообразования фондовых опционов. Для волатильности будем использовать значение OV. Если безрисковая ставка R = 6% и доля года, оставшаяся до истечения срока, Т = 0,25, то из (5.03) получим:

Полученное значение подставим в уравнение (5.05). Теперь для расчета дельты колл-опциона решим уравнение (3.21):

Подставим значения Y и N'(1,967087528) в уравнение (3.21) для получения дельты колл-опциона, в соответствии с уравнением (5.05):

Таким образом, когда цена портфеля равна 100, цена исполнения 100, доля года, оставшаяся до истечения срока исполнения, составляет 0,25, безрисковая ставка равна 6%, а волатильность портфеля 785,3069464%, дельта нашего гипотетического колл-опциона равна 0,9754135259. Сумма весов геометрического оптимального портфеля, состоящего из Toxico, Incubeast и LA Garb, найденная из уравнения (8.05), составляет 1,9185357. Таким образом, принимая во внимание уравнение (8.06), при страховании портфеля мы можем переразмещать до 50,84156244% (0,9754135359/ /1,9185357). Во сколько обходится страхование? Все зависит от волатильности в течение срока действия смоделированного опциона. Например, если за время действия смоделированного опциона баланс на счете не колеблется (волатильность равна 0), цена смоделированного опциона, т.е. стоимость страхования, равна нулю. В этом заключается большое преимущество страхования портфеля по сравнению с реальной покупкой пут-опциона (если этот пут-опцион по портфелю существует). Мы платим теоретическую цену опциона, исходя из той волатильности, которой реально подвержен портфель, а не той, которая существовала на рынке до открытия позиции, как бывает при покупке пут-опциона. Кроме того, реальная покупка пут-опциона (опять же, если пут-опцион по нашему портфелю существует) влечет за собой расходы, связанные со спредом покупки/продажи. При моделировании опциона таких расходов не возникает.

Содержание раздела