Подведение итогов
Отметим важный факт: структура неограниченного портфеля (для которого сумма весов больше 1, a NIC является частью портфеля) неизменна для любого уровня Е; единственным отличием является величина заемных средств (величина рычага).
Для портфелей, лежащих на эффективной границе, когда сумма весов ограничена, это не так. Другими словами, для любой точки на неограниченных эффективных границах (AHPR или GHPR) отношения весов различных рыночных систем всегда одинаковы.
Например, можно рассчитать отношения весов между различными рыночными системами в геометрическом оптимальном портфеле. Отношение Toxico к Incubeast составляет: 102,5982% / 49,00558% = 2,0936.
Таким же образом мы можем определить отношения всех компонентов в портфеле друг к другу:
Toxico / Incubeast = 2,0936
Toxico / LA Garb = 2,5490
Incubeast / LA Garb = 1,2175
Теперь вернемся к неограниченному портфелю и найдем веса для различных значений Е. Далее следуют веса компонентов неограниченных портфелей, которые имеют самые низкие дисперсии для данных значений Е. Заметьте, что отношения весов компонентов одинаковы:

Таким образом, мы можем утверждать, что эффективные границы портфелей с неограниченной суммой весов содержат одинаковые портфели с разным уровнем заемных средств (с разным плечом). Портфель, в котором меняется величина плеча для получения заданного уровня прибыли Е, когда снято ограничение суммы весов, будет иметь второй множитель Лагранжа, равный нулю, при сумме весов, равной 1. Теперь мы можем достаточно просто определить, каким будет наш неограниченный геометрический оптимальный портфель. Сначала найдем портфель, который имеет нулевое значение для второго множителя Лагранжа, когда сумма весов ограничена 1,00. Одним из способов поиска такого портфеля является процесс итераций. Получившийся в результате портфель поднимается (или опускается) рычагом в зависимости от выбранного Е для неограниченного портфеля. Значение Е, удовлетворяющее любому уравнению с (7.06а) по (7.06г), и будет тем значением, которое соответствует неограниченному геометрическому оптимальному портфелю. Для выбора геометрического оптимального портфеля на эффективной границе AHPR для портфелей с неограниченными весами, можно использовать первый множитель Лагранжа, который определяет положение портфеля на эффективной границе. Вспомните (см. главу 6), что одним из побочных продуктов при определении состава портфеля методом элементарных построчных преобразований является первый множитель Лагранжа. Он выражает мгновенную скорость изменения дисперсии по отношению к ожидаемой прибыли (с обратным знаком). Первый множитель Лагранжа, равный - 2, означает, что в этой точке дисперсия изменяется по отношению к ожидаемой прибыли со скоростью 2. В результате, мы получим портфель, который геометрически оптимален.
(7.06д) L1 = - 2,
где L1 = первый множитель Лагранжа данного портфеля на эффективной границе AHPR для портфелей с неограниченной суммой весов.
Теперь объединим эти концепции вместе. Портфель, который с помощью рычага перемещается вдоль эффективных границ (арифметических или геометрических) портфелей с неограниченной суммой весов, является касательным портфелем к линии CML, выходящей из RFR == 0, когда сумма весов ограничена 1,00 и NIC не используется. Итак, мы можем найти неограниченный геометрический оптимальный портфель путем поиска касательного портфеля для RFR = 0, когда сумма весов ограничена 1,00, а затем поднять рычагом полученный портфель до точки, где он становится геометрическим оптимальным. Но как определить, насколько повысить данный ограниченный портфель, чтобы сделать его эквивалентным неограниченному геометрическому оптимальному портфелю?
Вспомните, что касательный портфель находится на эффективной границе (арифметической или геометрической) портфелей с ограниченной суммой весов в точке с наивысшим отношением Шарпа (уравнение (7.01)). Мы просто повысим рычагом этот портфель и умножим веса каждого из его компонентов на переменную, называемую q, которую можно получить следующим образом:
(7.13) q=(E-RFR)/V,
где Е = ожидаемая прибыль (арифметическая) касательного портфеля;
RFR = безрисковая ставка, по которой вы можете занять или дать взаймы;
V= дисперсия касательного портфеля.
Уравнение (7.13) является достаточно хорошим приближением реального оптимального q.
Следующий пример может проиллюстрировать роль оптимального q. Вспомните, что наш неограниченный геометрический оптимальный портфель выглядит так:

Портфель имеет AHPR= 1,245694 и дисперсию 0,2456941. В оставшейся части нашего обсуждения мы будем исходить из того, что RFR = 0 (в данном случае отношение Шарпа этого портфеля, (AHPR-(1 + RFR)) / SD, равно 0,49568).
Теперь, если мы введем те же прибыли, дисперсии и коэффициенты корреляции компонентов в матрицу и рассчитаем, какой портфель находится в точке касания при RFR = 0, когда сумма весов ограничена 1,00 и при отсутствии NIC, то получим следующий портфель:

Этот портфель имеет AHPR = 1,128, дисперсию 0,066683 и отношение Шарпа 0,49568. Отметьте, что отношение Шарпа касательного портфеля, для которого сумма весов ограничена 1,00, при отсутствии NIC, в точности равно отношению Шарпа для нашего неограниченного геометрического оптимального портфеля.
Вычитая единицу из полученных AHPR, мы получаем арифметическую среднюю прибыль портфеля. Далее заметим: чтобы для ограниченного касательного портфеля получить прибыль, равную прибыли неограниченного геометрического оптимального портфеля, мы должны умножить веса первого на 1,9195.
0,245694/0,128=1,9195
Теперь, если мы умножим каждый из весов ограниченного касательного портфеля, то получим портфель, идентичный неограниченному геометрическому оптимальному портфелю:

Множитель 1,9195 получен в результате деления прибыли неограниченного геометрического оптимального портфеля на прибьыь ограниченного касательного портфеля. Как правило, нам надо найти неограниченный геометрический оптимальный портфель, зная только ограниченный касательный портфель. Именно здесь и используется оптимальное q. Если мы допускаем, что RFR = 0, то можно определить оптимальное q по нашему ограниченному касательному портфелю следующим образом:
(7.13) q=(E-RFR)/V=(0,128-0)/0,066683 = 1,919529715
Несколько замечаний по поводу RFR. Когда речь идет о фьючерсных контрактах, следует приравнять RFR к нулю, так как в действительности мы не занимаем и не ссужаем средства для увеличения или уменьшения активов портфеля. С акциями ситуация иная, и RFR следует принимать во внимание.
Вы часто будете использовать AHPR и дисперсию для портфелей на основе дневных HPR компонентов. В таких случаях необходимо применять не годовую, а дневную ставку RFR. Это довольно простая задача. Сначала необходимо убедится, что годовая ставка является эффективной годовой процентной ставкой.
Процентные ставки обычно указываются в годовых процентах, но часто они представляют собой номинальную годовую процентную ставку. Если процентная ставка складывается из полугодовых, квартальных, месячных ставок и т.д., то ставка, заработанная за год, будет больше, чем просто годовая ставка (номинальная). Когда процент суммируется, эффективная годовая процентная ставка может быть определена из номинальной процентной ставки. Полученную эффективную годовую процентную ставку мы и будем использовать в расчетах. Для преобразования номинальной ставки в эффективную ставку следует использовать формулу:
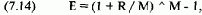
где Е = эффективная годовая процентная ставка;
R = номинальная годовая процентная ставка;
М == число периодов сложения за год.
Предположим, номинальная годовая процентная ставка составляет 9%, и доход по ней пересчитывается каждый месяц по формуле сложного процента. Соответствующая эффективная процентная ставка будет равна:
(7.14) Е = (1+0,09/12)^ 12-1 = (1 + 0,0075)^12-1 ==1,0075^12- 1 = 1,093806898 = 0,093806898
Таким образом, наша эффективная годовая процентная ставка будет немногим больше 9,38%. Теперь, чтобы рассчитать HPR на основе рабочих дней, мы должны найти среднее число рабочих дней 365,2425 /7*5= 260,8875. Разделив 0,093806898 на 260,8875, мы получим дневное RFR = 0,0003595683887.
Если мы на самом деле будем привлекать средства, чтобы получить из ограниченного касательного портфеля неограниченный геометрический оптимальный портфель, необходимо ввести значение RFR в отношение Шарпа, уравнение (7.01), и оптимальное q, уравнение (7.13).
Подведем итог. Допустим, RFR для вашего портфеля не равно 0, и необходимо найти геометрический оптимальный портфель, не рассчитывая ограниченный касательный портфель для этого RFR. Можете ли вы перейти прямо к матрице, установить сумму весов на какое-либо произвольно высокое значение, добавить NIC и найти неограниченный геометрический оптимальный портфель, когда RFR больше О? Да, если вычесть RFR из ожидаемых прибылей каждого компонента, но не из NIC (т.е. ожидаемая прибыль для NIC остается нулевой, что соответствует среднему арифметическому HPR= 1,00). Теперь, решив матрицу, мы получим неограниченный геометрический оптимальный портфель, когда RFR больше 0.
Так как эффективная граница для портфелей с неограниченной суммой весов дает один и тот же портфель с различной величиной рычага, линия CML не может пересекаться или касаться эффективной границы портфелей с неограниченной суммой весов, если же сумма весов ограничена (т.е. равна 1) — это возможно.
Мы рассмотрели несколько способов определения геометрического оптимального портфеля. Например, мы можем рассчитать его эмпирически, что было продемонстрировано в книге «Формулы управления портфелем» и повторено в первой главе этой книги. В данной главе мы узнали, как с помощью параметрического метода рассчитать портфель при любом значении безрисковой ставки.
Теперь, когда мы знаем, как определить геометрический оптимальный портфель, рассмотрим его использование в реальной жизни. Геометрический оптимальный портфель даст нам максимально возможный геометрический рост. В следующей главе мы рассмотрим способы использования этого портфеля при заданных рисковых ограничениях.
Содержание раздела