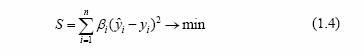В практических исследованиях в качестве модели тренда в основном используют следующие функции: линейную у = ax + b;

квадратичную у = ах2 + bх + с; степенную у = aхn; показательную у

= ax; экспоненциальную у = аеx; логистическую у =

Особенно широко применяется линейная, или линеаризуемая, т.

е. сводимая к линейной, форма как наиболее простая и в достаточ-

ной степени удовлетворяющая исходным данным.

Выбор модели в каждом конкретном случае осуществляется по

целому ряду статистических критериев, например по дисперсии,

корреляционному отношению и др. Следует отметить, что назван-

ные критерии являются критериями аппроксимации, а не прогноза.

Однако, принимая во внимание принятую гипотезу об устойчивости

процесса в будущем, можно предполагать, что в этих условиях мо-

дель, наиболее удачная для аппроксимации, будет наилучшей и для

прогноза.

Классический метод наименьших квадратов предполагает рав-

ноценность исходной информации в модели. В реальной же практи-

ке будущее поведение процесса значительно в большей степени оп-

ределяется поздними наблюдениями, чем ранними. Это обстоятель-

ство породило так называемое дисконтирование, т. е. уменьшение

ценности более ранней информации. Дисконтирование можно

учесть путем введения в модель (1) некоторых весов β < 1. Тогда

Коэффициенты β, могут задаваться заранее в числовой форме

или в виде функциональной зависимости таким образом, чтобы по

мере продвижения в прошлое веса убывали, например i

i β = a , где а

< 1. К сожалению, формальных процедур выбора параметра не раз-

работано, и он выбирается исследователем произвольно.

Метод наименьших квадратов широко применяется для получе-

ния конкретных прогнозов, что объясняется его простотой и легко-

стью реализации на ЭВМ. Недостаток метода состоит в том, что мо-

дель тренда жестко фиксируется, и с помощью МНК можно полу-

чить надежный прогноз на небольшой период упреждения. Поэтому

МНК относится главным образом к методам краткосрочного про-

гнозирования. Кроме того, существенной трудностью МНК является

правильный выбор вида модели, а также обоснование и выбор весов

во взвешенном методе наименьших квадратов.

1. В чем состоит сущность метода наименьших квадратов?

2. Назовите основные предпосылки МНК, уточнение которых явля-

ется обязательным для получения наилучших оценок параметров

временного ряда.

3. В чем состоят достоинства МНК?

Метод наименьших квадратов 2