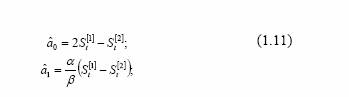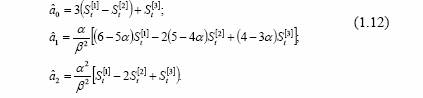|
|

|
|
|
для квадратичной модели –
Прогноз реализуется по выбранному многочлену. Соответственно для линейной модели
для квадратичной модели
где τ - период прогноза. Важную роль в методе экспоненциального сглаживания играет выбор оптимального параметра сглаживания α , так как именно он определяет оценки коэффициентов модели, а, следовательно, и результаты прогноза [72, 103, 215]. В зависимости от величины параметра прогнозные оценки по разному учитывают влияние исходного ряда наблюдений: чем больше α , тем больше вклад последних наблюдений в формирование тренда, а влияние начальных условий быстро убывает. При малом α прогнозные оценки учитывают все наблюдения, при этом уменьшение влияния более «старой» информации происходит медленно. Известны два основных соотношения, позволяющие найти приближенную оценку α . Первое соотношение Брауна, выведенное из условия равенства скользящей и экспоненциальной средней
α , где N – число точек ряда, для которых динамика ряда считается однородной и устойчивой (период сглаживания). Вторым является соотношение Мейера
α ≈ n , где n σ - среднеквадратическая ошибка модели; ε σ - среднеквадратическая ошибка исходного ряда. Однако использование последнего соотношения затруднено тем, что достоверно определить n σ и ε σ из исходной информации очень сложно. |
Метод экспоненциального сглаживания 3 |