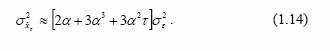|
|

|
|
|
Выбор параметра α целесообразно связывать с точностью прогноза, поэтому для более обоснованного выбора α можно использовать процедуру обобщенного сглаживания, которая позволяет получить следующие соотношения, связывающие дисперсию прогноза и параметр сглаживания [103, 129]. Для линейной модели –
Для квадратичной модели –
Для обобщенной модели вида
Дисперсия прогноза имеет следующий вид
где ε σ – среднеквадратическая ошибка аппроксимации исходного динамического ряда; fi(t) – некоторая известная функция; V– матрица ковариации коэффициентов модели. Отличительная особенность этих формул состоит в том, что при α = 0 они обращаются в нуль. Это объясняется тем, что, чем ближе к нулю α , тем больше длина исходного ряда наблюдений t → ∞ и, следовательно, тем меньше ошибка прогноза. Поэтому для уменьшения ошибки прогноза необходимо выбирать минимальное α . В то же время параметр α определяет начальные условия, и, чем меньше α , тем ниже точность определения начальных условий, а следовательно, ухудшается и качество прогноза. Ошибка прогноза растет по мере уменьшения точности определения начальных условий [103]. |
Метод экспоненциального сглаживания 4 |