|
|

|
|
|
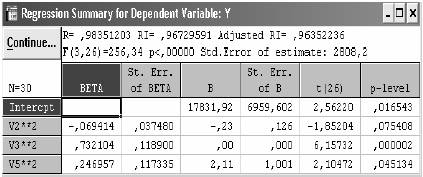
Нажимаем кнопку Regression summary и получим следующее диалоговое окно «Суммарная регрессия для зависимой переменной Y»
Рисунок 3.21. Суммарная регрессия для зависимой переменной Y
Очевидно, что данная модель не является оптимальной и наилучшей, но если рассмотреть коэффициент множественной детерминации RI = 0,97, то можно сказать, что он выше, чем у наилучшей линейной модели. Можно сделать вывод о том, что неучтенных факторов всего 3%. Что касается адекватности модели, то модель является адекватной, так как FP > FT (при степенях свободы v1 = 3 и v2 = 26 имеем 256,34 > 2,98), но на ее основе нельзя осуществлять прогнозы, так как она включает в себя незначимый фактор – х1 2. Уравнение регрессии будет иметь следующий вид
Если проанализировать его, то можно сказать, что знаки коэффициентов, стоящих перед факторными признаками, экономически верны: чем выше процент реализации халвы, тем ниже убытки, и чем больше стоимость сырья и его расход, тем выше убытки предприятия. Для того, чтобы оптимизировать и улучшить модель, необходимо исключить незначимый фактор х1 2. После его исключения уравнение регрессии примет следующий вид
|
Нелинейные многофакторные модели 3 |