Использование методов преобразования распределений в расчетах заработной платы

Пример 1. Допустим, что интервал 400-900 руб., частость для которого равна 30, необходимо раздробить на два интервала: 400-600 и 600-900 руб.
При условии равномерного распределения внутри интервала можно составить следующую пропорцию: величине известного интервала с_ь равной 500 руб., соответствует частость/_ь равная 30%, а
заданной величине интервала с(^, равной 200 руб.,искомая частость /(Р, откуда
200x30
500
(О ₌
= 12%-
Это есть не что иное, как эмпирическая плотность вероятностей исходного интервала, T.e./^xj).
Следует помнить, что плотностью исходного интервала можно пользоваться лишь в его пределах. Пусть требуется рассчитать частости для интервалов 400-600 и 600-1000 руб. при С! = 50, с₂ = 40, частости для интервала 400-900 руб. при с = 30 и для интервала 900-1300 руб. при с = 50,5.

Имея плотность интервала 400-900 руб., равную 0,6, определяем частость интервала 400-600 руб. как 20 х 0,6= 12%. Но частость интервала 600-1000 руб. нельзя рассчитать, пользуясь этой же плотностью, так как ее действие распространяется лишь до 900 руб. Поэтому частость интервала 600-1000 руб. может быть определена как сумма частостей двух интервалов: 600-900 руб., имеющего частость 0,6 х 30 = 18%, и 900-1000 руб. с 50,5
частостью -х 10 = 12,6%. Таким образом, частость интервала
40
600-1000 руб. составляет 18 + 12,6= 30,6%.
Обратная этой задача состоит в расчете интервалов распределения, соответствующего заданным частотам (частостям). Она решается с помощью преобразования второго рода, основанного на величине, обратной эмпирической плотности распределения и равной отношению длины интервала (с) к частоте щ или частости f. Величина искомого интервала с(^,
соответствующего заданной частоте (частости), рассчитывается по формулам:
д') ₌_L
,0).
-??
/w(*,)
_ /-(О - * г
Г 1
(9)
до _ ?i
(О
Пример 2. Часть интервала 400-900 руб., соответствующая час-
500
тости 14% от начала интервала, равна -х 14 233 руб. Значит,
30
границы искомого интервала составят 400-630руб.
Преобразования первого и второго рода применяются к одному и тому же распределению и его вида не меняют (характеристики преобразованного распределения остаются неизменными по сравнению с исходными). Другой характер носят такие преобразования, с помощью которых из одного распределения можно получить другое, функционально с ним связанное.

Это делается путем соответствующего пересчета либо частот (преобразование третьего рода), либо плотностей (преобразование четвертого рода), либо интервалов (преобразование пятого рода) исходного ряда распределения.
Если необходимо перейти от частот известного распределения wi к частотам распределения того же признака, но для другой совокупности w₂ при условии, что искомые частоты связаны с этим признаком, нужно последние умножить на Ф(*і), т.е.
w₂ = w,O(x0;/2 = /ІФ(*,), (10)
где Ф(*і) некоторая функция от*,.
Переход к плотностям в этом случае осуществляется обычным порядком путем деления частостей на величину интервалов.
Пример 3. Пользуясь данными табл. 2 (гр.

1, 2 и 3), рассчитаем распределение членов семей по душевому доходу.
Расчет частот (частостей) и плотностей распределения членов семей по душевому доходу

Таблица 2

Интервал душевого дохода в расчете на семью *2, РУб.	Число семей w₂, тыс.	Раз мер семей Ф*2, чел.	Число членов семей х₂, тыс. чел.	Частость на члена семьи, %	Величина интервала, руб.	Плот ность на члена семьи Ахг)
1	2	3	4	5	6	7
400-800	96	5,5	528	35,0	400	0,88
800-1120	38	4,5	171	11,3	320	0,35
1120-1440	239	3,0	717	47,5	320	1,48
1440-1760	22	2,5	55	3,6	320	0,11
1760-2080	20	2,0	40	2,6	320	0,08
Всего...	415	3,6	1511	100,0

Частота в этом распределении будет равна произведению числа семей на их размер, т.е. 96x5,5=528; 38x4,5 = 171 и т.д. Отнесение этих величин к итогу даст частости, а деление последних на величину интервалов плотности (см. табл. 2).
Можно также рассчитать плотность распределения какого-либо признаках^ по известной плотности признаках:!, связанного с Х2 функционально, т.е. при х:₂=Ф(х:і). Частота (частость) в интервале (x_{L Л}; х) для х\ равна произведению величины этого интервала
Х/_і -Хі = Сі, = Ахі
на его плотностьДхі), т.е.
При условии, что JC2 функция от хь изменение интервала, равное Дхь влечет изменение интервала другого признака, равное Л*2. Плотность же распределения этого признака будет равна частоте w\₉ деленной на величину интервала Лх₂, а именно:
(И)
/(Х\ )Ах, Ах₂
По формуле (11) исходная плотность корректируется с учетом соотношения интервалов исходного и искомого распределений. Заменяя Дхі и Дх2 на dxi и 6x2, получаем формулу плотности непрерывного признака *2, функционально связанного с непрерывным признаком х\\
Д*2) = /(*і)х-~- (12)

u^2
dx_xdx-у
Отношение
положительно, если интервалы исходного
и искомого признака связаны прямо пропорциональной зависимостью, и отрицательно, если существует обратно пропорциональная связь. Для расчета же значений плотности следует использовать абсолютную величину этого соотношения, т.е.
'*2
модуль производной
Пример 4. По данным табл. 2 (гр. 1 и 3) и примера 3 рассчитаем плотности распределения членов семей по душевому денежному доходу в интервале (руб.): 400-800; 800-1120; 1120-1440; 1440-1760; 1760-2080, имея в виду, что величина душевого денежного дохода функционально связана с размером заработной платы.
По формуле (11) определяем плотность первого интервала дохода (табл. 3).
Расчет плотностей распределения членов семей по душевому денежному доходу

Таблица 3

Интервал заработ ной платы, руб.	Величина интервала Ах], руб.	Частость на члена семьи, %	Плот ность ем	Интервал душевого дохода, руб.	Величина интерва ла, А *2	Плот ность Ахг)
400-900	500	35,0	0,070	400-800	400	0,88
900-1300	400	11,3	0,028	800 1120	320	0,35
1300-1700	400	47,5	0,118	1120 1440	320	1,48
1700-2100	400	3,6	0,009	1440 1760	320	0,11
2100-2500	400	2,6	0,007	1760 2080	320	0,08
Всего...		100,0

500
0,7 X-= 0,88, где 0,7 плотность распределения заработной платы
400
в расчете на члена семьи в интервале 400-900 руб. (табл. 3).
Х2
Функция Ф(дг,) имеет вид х₂ = 0,8 х_и откуда дг, = - *-. Следова-
0,8
тельно, расчет Дх₂) можно осуществить по формуле (13), в которой
jCj = = 1,25 иХх₂)= 1,25Дхі) (см. табл. 3).
0,8
Примененное здесь преобразование является обратным по отношению к преобразованию пятого рода, в котором рассчитываются не частоты, а интервалы, функционально связанные с интервалами исходного распределения. В данном случае х₂ = 0,8*1, х2 = 800, 1120, 1440,..., 2080.
При исходных частостях это дает исчисленные в табл. 3 плотности:
21 = 0,088; Ш = 0,035 ит.д.
Формы функциональных зависимостей плотностей или интервалов двух распределений могут быть и более сложными (выражаться многочленом, нелинейными функциями и т.д.).
Рассмотрим конкретные методы, основанные на описанных преобразованиях распределений и используемые в моделировании заработной платы.

§ 2. Использование методов преобразования распределений в расчетах заработной платы

Расчет распределения заработной платы с учетом условий оплаты труда. Этим методом осуществляется построение распределения рабочих и служащих по размерам заработной платы на основе заданных условий оплаты труда и структуры рабочей силы.
В соответствии с существовавшей системой заработной платы в СССР (с некоторыми непринципиальными изменениями действующей и поныне на предприятиях с государственной собственностью на средства производства (госпредприятиях) труд рабочих оплачивался по тарифным сеткам, различающимся для сдельщиков и повременщиков, отраслей народного хозяйства и т.д. В промышленности, в частности, действовало 12 тарифных сеток.
Каждая тарифная сетка делилась на несколько тарифных ставок. Тарифная ставка это размер оплаты за единицу времени (час, рабочий день, месяц) определенной работы, которая по сложности и важности отнесена к данному разряду. Перечень работ и условий труда, соответствующих каждому разряду, содержится в тарифно-квалификационных справоч-
никах. Тарифные условия различаются также по видам труда (нормальному, тяжелому, особо тяжелому и др.).
Для каждой отрасли установлены, как правило, тарифные ставки I разряда и межразрядные коэффициенты, т.е. отношения каждой последующей ставки к первой. Таким образом, если число разрядов в тарифной сетке равно п, то, помимо ставки I разряда, в ней будет содержаться п - 1 различных межразрядных коэффициентов. Однако можно рассчитать и единый для данной сетки межразрядный коэффициент ()
либо как среднюю геометрическую из отдельных межразрядных коэффициентов:
К{_еМ) =-jK_]K₂...K_n__], (14)
либо из отношения максимальной ставки к минимальной:
_К(Ю_{= (15)}
V ^min
Имея единый межразрядный коэффициент и тарифную ставку I разряда, можно приближенно находить тарифную ставку любого разряда по формуле
Т₍=Т_х(К(Р)‘-\ (16)
Пример 5. Для шестиразрядной сетки с соотношением в ставках VI и I разрядов 2:1
К(І?)=У2= 1,149.
При Т,=700 руб. Т₄ = 700 х 1,1493 = 1062 руб.
Тарифная ставка важнейший фактор формирования заработной платы работников госпредприятий. При этом у повременщиков заработок равен тарифной ставке при усло-56
вии целиком отработанного нормативного времени, у сдельщиков при стопроцентном выполнении нормы выработки. Поэтому другим важным фактором формирования заработной платы рабочего-сдельщика является величина нормы выработки и уровень ее выполнения.

Заработок, исчисленный с учетом выполнения нормы выработки, называют сдельным. Его можно рассчитать двояко с использованием сдельной расценки либо с учетом индекса выполнения норм выработки. Обозначим норму выработки в единицу времени через Н, а сдельную расценку через С.
Тогда
где к количество произведенной продукции в натуральном выражении.
Если известен индекс выполнения нормы выработки /,„ то 3_Сд = ТхІ_н. (19)
Системой оплаты труда предусмотрены также премии работникам за перевыполнение норм выработки, за срочную и высококачественную работу и т.д. Установлены они в процентах к тарифному заработку, но могут быть рассчитаны и в процентах к сдельному (п_пр). Тогда основной заработок, т.е. заработок, включающий премии,
Зосн Т х І_н х п_Пр. (20)
Наконец, кроме премий заработная плата работников включает различного рода доплаты (например, за работу в ночное время, районные надбавки и др.). Их размер также можно исчислить в процентах к основному заработку (п_пд). Это позволит рассчитать полный заработок (З_п) следующим образом:
(21)
З_п Т х І_н х п_Пр х Пдд.
Описанный метод прямого счета, как видим, состоит в переходе по формуле (21) от тарифного заработка к сдельному, а затем к основному и к полному с помощью преобразования третьего рода. При этом для повременщиков и служащих такие переходы включают лишь расчет основного и полного заработков.
Пример 6. Рассчитаем распределение рабочих-сделыциков III разряда по размерам заработной платы в интервалах (руб.): до 900; 900-1300; 1300-1700; 1700- 2100; свыше 2100 при следующих условиях:
1. Тарифная ставка I разряда 800 руб.
2. Единый межразрядный коэффициент 1,15.
3. Распределение рабочих-сделыциков III разряда по выполнению нормы выработки таково:
Выполнение нормы выработки, % 80100 100150 150200
Сдельщики III разряда, %
20
70
10
Всего... 100
4. Условиями оплаты труда предусмотрена премия в размере 10% сдельного заработка при выполнении нормы выработки на 150% и выше.
5. Рабочие-сдельщики, выполняющие норму выработки на 150% и более, имеют также прочие доплаты, составляющие в среднем 5% основного заработка.
6. Общее число рабочих-сделыциков III разряда 1000 человек.
В соответствии с приведенными выше формулами рассчитываем для рабочих-сделыциков III разряда:
1) тарифную ставку: Т,„ = 800 х1,152* 1060 руб.;
2) распределение по сдельному заработку:
Рабочие-сдельщики,
%
20
70
10
Рабочие-сдельщики,
чел.
200
700
100
Сдельный заработок, руб.
850-1060
1060-1590
1590-2120
Всего 100 Всего 1000
Сдельный заработок определяем по формуле (19): 1060 х 0,8 = = 850 руб., 1060 х 1,0=1060 руб.; 1060 х 1,5=1590 руб. и т.д., где 0,8, 1,0 и 1,5 индексы выполнения нормы выработки;
3) распределение по основному заработку (с округлением до десятков):
Рабочие-сдельщики, Основной заработок,
чел. руб.
200 850-1060
700 1060-1750
100 1750-2330
Всего 1000
Основной заработок рассчитан по формуле (20): 1590 х 1,1 = = 1750 руб. и 2120 х 1,1 = 2330, где 1,1 отношение основного заработка к сдельному:
4) распределение по полному заработку (с округлением до десятков):
Полный заработок, руб.
850-1060
1060-1840
1840-2450
Рабочие-сдельщики, чел.
200 700 100
Всего 1000
Полный заработок рассчитан по формуле (21):
1750 х 1,05= 1840 руб., 2330 х 1,05 = 2450 руб.,
где 1,05 коэффициент прочих доплат.

Как видим, переходы 2-4 осуществлялись с помощью преобразования третьего рода. Чтобы перейти к распределению в заданных интервалах, применим преобразование первого рода. Получим:
5) распределение по полному заработку в заданных интервалах:
Полный заработок, руб. Рабочие-сдельщики, чел.

до 900	48
900-1300	367
1300-1700	359
1700-2100	169
Свыше 2100	57

Всего... 1000

Построение распределения рабочих и служащих по размерам заработной платы при заданном повышении ее минимума. В практике плановых расчетов заработной платы часто возникает задача построения ряда распределения при условии повышения ее минимума.
Специфика рядов распределения заработной платы, как будет показано ниже, состоит в том, что повышение минимума в них почти всегда связано с определенным увеличением заработной платы более высоких уровней. Задача поэтому может быть сведена к расчету ожидаемой трансформации всего базисного ряда распределения (его сжатия и сдвига) с учетом заданного изменения минимального и максимального уровней ряда, в качестве которых принимаются условные минимум и максимум. Решение этой задачи существенно облегчается, если базисный ряд распределения представить в виде строго упорядоченного ряда чисел. Применительно к заработной плате им является геометрическая прогрессия.
Следовательно, постановка задачи такова: на основе базисного ряда распределения заработной платы рассчитать плановый ряд при условиях:
¦^шіп (а) -
X min О);
¦^max О ~ Р ^ % _max (1 ~' Р)ч
где x_min (а) условный минимум базисного ряда;
*max (1 - Р) условный максимум базисного ряда;
*min (or) и x’_max (1 -р) соответственно те же значения для планового ряда, причем х’_т{п (а) x_min (а), а х’_тах (1 - р) = ~ ^тах (1 Р)
Решение этой задачи основано на преобразованиях первого и третьего рода. Функциональная связь искомых и базисных интервалов строится на предположении линейного роста логарифмов заработной платы во времени. Ход решения таков:
1. Базисный ряд распределения пересчитывается в ряд, варианты которого нарастают в геометрической прогрессии. Для этого:
а) определяется знаменатель прогрессии q по формуле

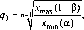
(23)
где п число интервальных групп базисного ряда распределения;
б) рассчитываются варианты (интервалы) ряда, нарастающие в геометрической прогрессии:
(24)
^тіп(^)хЧз 5
где іномер интервальной группы;
в) частоты (частости) базисного ряда с помощью преобразования первого рода пересчитываются в соответствии с интервалами, нарастающими в геометрической прогрессии.
2. Рассчитываются варианты планового ряда распределения, нарастающие в геометрической прогрессии.
Для этого: а) определяется д₃':
wQ-P).
^'шіп(а) ’
ft'
(25)
б) рассчитывается
(26)
*/' =*'mm () х (Ч'зУ '-
3. С помощью преобразования первого рода рассчитывается плановый ряд распределения в обычных интервалах. Расчет упрощается, если пользоваться не значениями заработной платы, а ее логарифмами и применить преобразование третьего рода.
Для этого прологарифмируем выражения (24) и (26):

	lg Xi = lg X_lnin () + (/- 1) lg qy,	(27)
	lg x'i = lg x'min (a) + (/ - 1) lg q'i,
откуда	lg, - lgx_min (a) = (/ - l)lg?3 = = -^-klg^max(1 - 3) - lg_min (a)]; n 1	(28)
	lg x] - lg x_min (a) = (/ -1) lg ?3 =
	= ^[lgx_max(l-0)-lgx_mjn(a)]; n 1	(29)

Отношение второго выражения к первому в формулах (28), (29) равно

(30)
4?*/ ^ё^тіп^) _ 4?/*imax О Р) *min foO
lg*, - lg*_min(a) lgJCmaxO-P) - Ig^min(a)
Обозначив правую часть выражения (30) через А, получим формулу, связывающую величины интервалов логарифмов базисного и планового рядов распределения заработной платы:
lg х\ = lg x'_min () + A (lg Xj lg x_min (a)). (31)
При
xmin (a) _ *max 0 P) *min (a) *max 0 " P)
*min (a) *max 0 ~~ P) *min(a) WO-P)
*min (a) *max 0 ~~ P) *min(a) ^maxO-P)
для A = 1;
дляА1; (32)
для A 1.
Поскольку обычно рассматривается третий случай, когда максимум растет медленнее минимума или вовсе не растет, а потому имеет место некоторое сжатие планового ряда распределения по сравнению с базисным, А называют коэффициентом сжатия, хотя правильнее называть его коэффициентом трансформации ряда распределения.
Использование коэффициента трансформации упрощает процедуру вычисления планового ряда распределения, которая в этом случае включает:
1) логарифмирование базисных интервалов заработной платы;
2) расчет коэффициента сжатия планового ряда распределения по формуле (30);
3) расчет логарифмов плановых интервалов заработной платы по формуле (31);
4) потенцирование логарифмов плановых интервалов заработной платы, которым соответствуют базисные частоты (частости);
5) пересчет базисных частостей (частот) с помощью преобразования первого рода.
Пример 7. Рассчитаем прогнозируемый ряд распределения по данным табл. 4, приняв а= 1, /? = 98,9, х'_тіп (а) = 1800,
*тах (1-уб) = 5б00‘.
Тогда
lg 5600 -lg 1800 lg 5600 - lg 1600
0,9059.
3.7482- 3,2553
3.7482- 3,2041
Прогноз ряда распределения по заработной плате

Таблица 4

Базисный ряд	lg	lg-*'/	Прогнозируемый ряд
-X/	f	X',	// Для Хі
До 1600	1,0	До 3,2041	До 3,2553	До 1800	1,0
1600 2000	9,0	3,2041 3,3010	3,2553 3,3451	1800-2204	4,5
2000 2400	17,9	3,3010 3,3802	3,3451 3,4148	2204-2599	13,5
2400 2800	20,5	3,3802 3,4472	3,4148 3,4755	2599-2988	19,6
2800 3200	18,0	3,4472 3,5051	3,4755 3,5280	2988-3373	19,9
3200 3600	13,1	3,5051 3,5563	3,5280 3,5744	3373-3754	15,9
3600 4000	8,7	3,5563 3,6021	3,5744 3,6158	3754-4129	11,7
4000 4400	5,3	3,6021 3,6435	3,6158 3,6534	4129-4502	6,2
4400 4800	3,0	3,6435 3,6812	3,6534 3,6875	45024870	3,6

Базисный ряд	ig-*,-	ig*',	Прогнозируемый ряд
Хі	/г	X',	/, ДЛЯ X,
4800 5200	1,6	3,6812 3,7160	3,6875 3,7190	4870-5236	2,0
5200 5600	0,8	3,7160 3,7482	3,7190 3,7482	5236-5600	1,0
Свыше 5600	и			Свыше 5600	и

lg*', рассчитаны по формуле (31). Например,
lg х'₂ = 3,2553 + 0,9059(3,3010 3,2041) = 3,3451;
lg х'з = 3,2553 + 0,9059(3,3802 3,2041) = 3,4148 и т.д.

/і ~ fi ’
(2000 - 1800)= 4,5;
2200 1800 9
17,9
(2200 - 2000) +
-х 100 =
2200 - 1800
2599 - 2400
= 4,5 4- 9 = 13,5.
и т.д.;
/і2 = f\2 *

§ 3. Использование методов преобразования распределений в расчетах доходов семей

Сущность композиции статистических данных. Показатели уровня жизни отличаются большой разнородностью взаимосвязей. Например, для расчета семейных доходов нужны данные о заработной плате работающих членов семей, о числе работающих и иждивенцев в семьях, о размере прочих доходов, поступающих членам семей, и др.

Необходимо, кроме того, всех работающих членов семей разделить на первых (т.е. получающих наибольшую заработную плату), вторых, третьих работников и т.д. Подробные сведения такого рода
можно найти в единовременных и бюджетных обследованиях населения, но репрезентативность этих источников сомнительна в силу их малочисленности. Напротив, сплошные данные переписи населения, текущей статистики, финансов, просвещения, здравоохранения и т.д. достоверны, но содержат ограниченное число показателей (либо только о составе семей, либо только о величине потребляемых ими услуг здравоохранения, просвещения и т.д.).

В связи с этим в процессе анализа и прогнозирования уровня жизни возникает необходимость композиции статистических данных, полученных из различных источников.
В основе статистической композиции лежит группировка, позволяющая получить нужные статистические данные на основе аналитических показателей, содержащихся в отдельных источниках. Например, пользуясь выборочными показателями, связывающими состав семей и их доходы с данными о семейном составе всего населения, можно рассчитать распределение всех семей по доходу.

Но связь состава и доходов семей может быть выявлена на основе бюджетных обследований, а семейный состав населения на основе всеобщей переписи.
Если обозначить распределение населения по доходу через R = F(x), а его половозрастную структуру через 8=ДВ), то произведение RSдаст новую функцию распределения
y = R8 (33)
Такого рода композиция дает возможность получить необходимые сведения. Метод, позволяющий осуществить эту композицию, основан, как нетрудно заметить, на описанных выше преобразованиях частот распределений.
Пример 8. Композиция статистических данных в расчетах распределения семей по доходу. Пусть имеется следующее исходное распределение работников по уровню заработной платы (полу-
66
ценное на основе статистических данных или с применением соответствующих функций распределения):
Всего 1000
Предположим, что в результате специальной обработки результатов выборочного обследования семей рабочих и служащих выявлены следующие данные (табл. 5, 6, 7, 8)1.
Распределение работников на первых и прочих работников (в %)

Таблица 5

Интервал заработной платы, руб.	Первые работники	Прочие работники	Всего
700ЮОО	30	70	100
10001500	40	60	100
1500 2000	50	50	100
2000 3000	80	20	100

Таблица 6
Удельное распределение семей по числу работников (один и более одного) и по размеру заработной платы первого и прочих работников

Интервал заработной платы первого работника, руб.	Семьи только с одним работником, %	Семьи с прочими работниками, заработная плата которых находится в интервале, руб. (в %)	Всего, %
700 1000	1000 1500	1500 2000	2000 3000
700-1000	70	30				100
1000-1500	60	25	15			100
1500-2000	55	20	20	5		100
2000-3000	50	15	15	10	10	100

1 О факторах формирования семейных денежных доходов см. в гл. 3,§3.
Удельное распределение семей по величине получаемых ими доплат

Таблица 7

Интервал совокупной заработной платы, руб.	Семьи без прочих доходов, %	Семьи с прочими доходами, в интервале, руб. (в %)	Всего, %
300-500	500-700	700 1000
700-1500		60	30	10	100
1500-3000	10	50	40		100
3000-4500	20	70	10		100
4500-6000	40	60			100

Удельное распределение семей по числу членов

Таблица 8

Интервал полного денежного дохода, руб.	Семьи, %, состоящие	Всего, %
из двух человек	из трех человек	из четырех человек
1000-2000	50	30	20	100
2000-3000	70	20	10	100
3000-4500	80	20		100
4500-6500	90	10		100

Рассчитаем распределение семей работников по душевому доходу на основе приведенного выше распределения по заработной плате и данных табл. 5-8.
Данные табл. 6 позволяют осуществить первую композицию определить число семей в заданных интервалах заработной платы их первого работника. Очевидно, что семей будет столько же, сколько первых работников, а именно: в интервале 700-1000 руб.

Содержание раздела