МЕХАНИЗМЫ ФОРМИРОВАНИЯ ФОНДА ЗАРАБОТНОЙ ПЛАТЫ
А.5. Функция полезности u(q, t) непрерывно дифференцируема, частично строго монотонна и имеет убывающие и выпуклые кривые безразличия.
Если у агента отсутствуют нетрудовые доходы (non-wage income), то его доход равен заработной плате и однозначно определяется продолжительностью рабочего времени, то есть q(t) = s(t).
продолжительности рабочего времени от ставки оплаты (кривая обратного изгиба)
Обозначим g - некоторый фиксированный уровень полезности (см. рисунок 18). Если уравнение u(q, t) = g разрешимо относительно q, то можно получить уравнение кривой безразличия:
q = v(g t). Обозначая u't = ^(q’t) , u'q = ^uUq’lt , получаем выраже-
8t dq
ние для производной кривой безразличия:
(1) dl = - u't / u'q .
У ’ dt t q
Если a - постоянная ставка оплаты, то кривая бюджетного ограничения q(t) = S(t), где о(-) - функция стимулирования, имеет вид прямой (см. рисунок 18):
(2) q(t) = a t = a (T- t).
Агент решает задачу выбора такого значения t времени досуга (и, соответственно, рабочего времени t = T - t*), которое максимизировало бы его полезность:
(3) t* е Arg max u(q(t), t),
te[0;T ]
где q(t) определяется выражением (2). Необходимое условие оптимальности - равенство нулю производной по t выражения u(q(t), t):
U'q + U't = 0.
dq dt
Подставляя (2), запишем условие оптимума следующим образом:
(4) u’t = a u’q.
Условие (4) в литературе по предложению труда называется Roy’s Identity [136].
Воспользовавшись (1), получаем, что необходимое условие оптимальности графически можно интерпретировать как условие касания кривой безразличия прямой бюджетного ограничения (см. рисунок 18).
Рис. 18. Кривые безразличия для значений полезности у1 и у2, бюджетное ограничение и условие оптимальности
Отметим, что (4) является условием оптимума при внутренних решениях задачи (3). Если максимум в выражении (3) достигается при t = T (граничное решение), то говорят, что имеет место угловое решение [96, 113].
Содержательно, угловое решение соответствует оптимальности для рассматриваемого агента решению не работать вообще, так как любой час своего досуга (в том числе и шестнадцатый) он ценит выше предлагаемой ставки оплаты. На рисунке 19 изображено угловое решение, то есть при ставке резервной
заработной платы а и величине нетрудовых доходов qT (доходов агента, не зависящих от количества отрабатываемых часов, например - рента, пособия и т.д.) кривая безразличия g касается прямой бюджетного ограничения в точке А (t = T - см. рисунок 19).
Рис. 19. Угловоерешение
Рассмотрим пример, иллюстрирующий применение описанного метода определения оптимального времени досуга.
Пример 3. Пусть функция полезности имеет вид: u(q, t) = b q t, где Ь - некоторая положительная константа. Кривой безразличия
g 1
g в данном случае является гипербола: q(t) = . Из условия (4)b t Из выражения (5) следует, что имеют место и эффект дохода:
dt (a, g) dg
dt (a, g) da
?0, и эффект замещения:
0.
g=Const
a=Const
Существуют два способа поиска оптимального времени досуга
га. Первый заключается в использовании условия (4): = a.
dt
Проверяя, что оптимально внутреннее решение (u(0) = u(T) = 0), получаем: t = T/2.
Второй способ заключается в лобовом решении задачи максимизации полезности (см. (3)):
t* = arg max u(q(t), t) = arg max [aB t (T- t) } = T/2.
te[0;T ] te[0;T ]
Интересно отметить, что при рассматриваемой функции полезности оптимальное решение t* равно восьми часам и не зависит от ставки оплаты. В то же время, максимальное значение полезности u = apT2/4 возрастает с ростом ставки оплаты. -
Напомним, что до сих пор мы рассматривали модели индивидуального поведения на рынке труда в предположении, что за каждый отработанный час агент получает одинаковую оплату (ставка оплаты считалась постоянной). Откажемся от этого предположения, то есть расширим класс допустимых систем стимулирования (любая система стимулирования может рассматриваться как пропорциональная с переменной ставкой оплаты).
Кроме того, установим взаимосвязь между базовыми системами стимулирования, рассмотренными в первой части настоящей работы, и описанием индивидуального поведения на рынке труда в рамках предпочтений на множестве доход - свободное время.
Действием агента будем считать продолжительность рабочего времени t, которая однозначно определяет продолжительность свободного времени: t = T - t, то есть y = t, A = [0; T]. Предположим, что центр использует некоторую (не обязательно пропорциональную) систему стимулирования s(t).
Определим функцию оплаты свободного времени s (t) = s(T - t). Отметим, что, если о(-) - возрастающая (убывающая, выпуклая, вогнутая) функция, то (t) - убывающая (соответственно, возрастающая, выпуклая, вогнутая) функция.
Если функция стимулирования задана, то, фактически, можно считать, что задана и зависимость дохода от свободного времени:
q(t) = S (t) = o(T - t).
Определяя наиболее предпочтительное (с точки зрения значения своей функции полезности u(q, t)) значение продолжительности рабочего времени, агент решает следующую задачу:
(6) u(q, t) = u(o(T- t), t) ® max .
te[0;T ]
Предполагая существование внутреннего решения t (t e (0; T)), получаем необходимое условие оптимальности:
u
(7) -+ = - ~(t) = s (T -1) = s (t).
Uq
Левая часть выражения (7) с точностью до знака совпадает с производной кривой безразличия функции полезности, следовательно в точке оптимума графики кривой безразличия полезности u(-) и функции стимулирования (- ) должны иметь общую касательную. Содержательно это утверждение означает, что предельный доход должен быть равен предельному стимулированию
(dqjt*)
( dt
ds (t) dt
), то есть в точке оптимума альтернатив-
t=t-t * ная стоимость единицы свободного времени по абсолютной величине равна скорости изменения вознаграждения.
Второй важный (и достаточно очевидный) вывод, который следует из анализа выражения (7), заключается в том, что в точке оптимума t = T-1 производная функции стимулирования o(t) должна быть положительна (так как положительны обе производные функции полезности, фигурирующие в левой части (7); действительно, выше предполагалось, что полезность агента возрастает как с ростом дохода, так и с увеличением продолжительности свободного времени). Более того, так как рабочим оказывается участок функции стимулирования с положительной производной, то в рамках рассматриваемой модели для любой функции стимулирования найдется монотонная (неубывающая) функция стимулиро-
вания, побуждающая агента выбрать то же действие. Следовательно, справедливо следующее утверждение.
Утверждение 6. Если выполнены предположения А.1-А.5, то при решении задач синтеза оптимальных функций стимулирования достаточно (без потери эффективности) ограничиться классом неубывающих функций стимулирования.
Это утверждение вполне согласовано со здравым смыслом и практическим опытом - большим значениям действий (отработанному времени) должно соответствовать большее вознаграждение.
Рассмотрим интерпретации базовых систем стимулирования в терминах функции полезности, принимая во внимание, что выше мы предположили, что кривые безразличия функции полезности u(q, t) агента убывающие и выпуклые.
Системы стимулирования K-типа.
Напомним, что компенсаторной выше была названа система стимулирования, которая компенсирует затраты агента, обеспечивая ему некоторый уровень полезности (например, полезность резервной заработной платы U ). Множество допустимых вознаграждений агента при ограничении C механизма стимулирования заштриховано на рисунке 20.
Если центр гарантирует агенту значение полезности, равное полезности резервной заработной платы, то компенсаторная система стимулирования oK(t) может быть найдена из следующих соот-
ношений (см. определение множества реализуемых действий выше):
(8) t: (T- t) е P(C) u( SK (t), t) = U ,
(9) ек(т) = SK (T -1).
Рис. 20. Множество допустимых вознаграждений АЭ
Из (8) следует, что график функции ~к (t) совпадает с кривой
безразличия функции полезности, определяемой условием: g = U (см. рисунок (21)). Так как кривая безразличия - убывающая и выпуклая, следовательно компенсаторная система стимулирования (а также, как мы знаем из результатов первой главы, функция затрат агента) является возрастающей и выпуклой (см. рисунок 21).
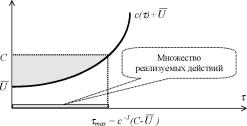
Кривая безразличия, соответствующая гарантированной полезности агента U , на рисунке 21 выделена жирной линией.
На рисунке 21 также изображена (жирной штрих-пунктирной линией) компенсаторная функция стимулирования к(1), соответствующая данной функции полезности агента (отметим, что при 1 tmax = T - tmin = c-I(C - U ) компенсаторное вознаграждение превысит ограничение C).
Итак, компенсация затрат в модели индивидуальных предпочтений означает, что агент находится на изокванте полезности и безразличен между всеми продолжительностями рабочего времени. Если выполнена гипотеза благожелательности, то он выберет продолжительность рабочего времени, оговоренную в контракте.
Рис. 21. Компенсаторная функция стимулирования
Приведем доказательство оптимальности систем стимулирования К-типа (в задачах первого и второго рода) в терминах функции полезности. Пусть центр хочет побудить агента отработать t часов.
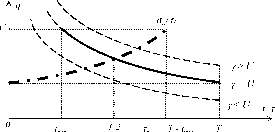
Свободное время при этом равно t = T - t. Наличие резервной заработной платы ограничивает множество возможных значений вознаграждения полуинтервалом АВ (см. рисунок 22).
Задача синтеза оптимальной функции стимулирования сводится к поиску такого бюджетного ограничения, которое касалось бы некоторой кривой безразличия на отрезке АВ, причем желательно, чтобы величина вознаграждения в точке касания была минимальна, то есть чтобы точка касания находилась как можно ближе к точке А, а в идеале - совпадала бы с ней. Кривая безразличия, проходящая через точку А, соответствует ограничению резервной заработной платы.
Если рассматривать ее саму как бюджетное ограничение, то получим, что последнему соответствует именно компенсаторная система стимулирования. При ее использовании затраты на стимулирование по реализации действия t равны qA (см. рисунок 22).
Если попытаться найти оптимальную пропорциональную систему стимулирования, реализующую то же действие t, то получим, что соответствующим ей бюджетным ограничением является
прямая, касающаяся кривой безразличия g g = U в точке С (см. рисунок 22). Через точку С проходит кривая безразличия, соответ-72
ствующая строго большей полезности, чем полезность резервной заработной платы. Поэтому, хотя пропорциональная система стимулирования и реализует действие t, она реализует его с затратами на стимулирование qC, строго большими, чем минимально необходимые.
Разность qC - qA показывает насколько переплачивает центр при использовании пропорциональных систем стимулирования по сравнению с компенсаторными. Аналогичные рассуждения можно привести, иллюстрируя их графиками (см. ниже), и относительно эффективности других базовых систем стимулирования в сравнении с компенсаторными и друг с другом.
Рис. 22. Оптимальность функции стимулирования К-типа
Из всех базовых систем стимулирования только компенсаторные зависят непосредственно от затрат агента. Поэтому при рассмотрении остальных базовых систем стимулирования учет полезности агента будет производиться не столь явным образом, как это делалось выше для компенсаторных. Реализуемое действие будем обозначать как и ранее t (t = T - t*).
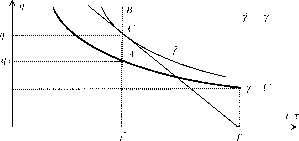
Аналогия приводимых ниже результатов с результатами анализа пропорциональных систем стимулирования следующая - функция поощрения ~(t) является бюджетным ограничением, которого в точке оптимума должна касаться кривая безразличия агента.
Системы стимулирования С-типа.
Напомним, что при использовании скачкообразных систем стимулирования oC(t) агент поощряется на фиксированную величину только в том случае, если его действие (продолжительность рабочего времени t) не меньше, чем заданный норматив х. Соответствующая функция c (t) определяется следующим образом: агент поощряется на фиксированную величину только в том случае, если продолжительность его свободного времени t не больше, чем заданный норматив х.
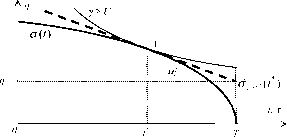
На рисунке 23 представлены: скачкообразная система стимулирования Sc (t) со скачком в точке х; кривая безразличия g = U полезности обозначена пунктиром, она совместно с ограничением механизма стимулирования c определяет минимальную продолжительность свободного времени tmin, которую центр может побудить выбрать агента; кривая безразличия функции полезности (соответствующая максимальному при данной системе стимулирования значению полезности агента) обозначена непрерывной линией, эта кривая безразличия характерна тем, что она касается ~c (t) в точке А.
Рис. 23. Скачкообразная функция стимулирования
Значение времени досуга, равное tmin, соответствует максимальной продолжительности рабочего времени, которое центр может побудить отработать агента, используя скачкообразные системы стимулирования, ограниченные сверху константой C (доход агента, равный C, при t = tmin обеспечивает ему минимальный уровень полезности, соответствующий резервной заработной плате).
Системы стимулирования L-типа (то есть линейные - с постоянной ставкой оплаты) подробно рассмотрены выше.
Остановимся более подробно на взаимосвязи сдельной и повременной оплаты. Как отмечалось выше (см. вторую главу), если результат деятельности агента, достигаемый за единицу времени (являющуюся основой отсчета при повременной оплате - минута, час, день и т.д.), постоянен и не зависит от количества уже отработанных часов, то с точки зрения теоретического анализа сдельная и повременная системы оплаты полностью эквивалентны - между ними существует линейная связь (то есть результат деятельности у прямо пропорционально рабочему времени т).
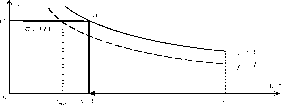
Если результат деятельности агента, достигаемый за единицу времени, зависит от количества уже отработанных часов, то между повременной и сдельной оплатой существуют различия.
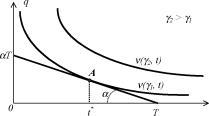
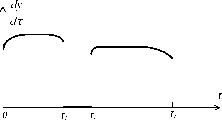
В работах зарубежных исследователей по экономике труда [101] обычно принимается следующий вид зависимости между результатами деятельности у и текущей продолжительностью рабочего времени т (см. рисунок 24). На рисунке 25 изображен dy(t)
график производной- кривой у(т) - кривая производительно-
dt
сти деятельности агента (результат деятельности, достигаемый в единицу времени).
Содержательно, низкая производительность в начале рабочего дня обусловлена эффектом врабатывания (или адаптации) -агент переключается (промежуток времени [0; ti]) на новый (по сравнению, например, с отдыхом) вид деятельности - работу. Постепенно производительность растет (промежуток времени [ту, т2], достигая максимума в момент времени т2 (или в более общем случае в некотором интервале времени). Затем, после мо-
мента времени Т2, начинает сказываться, например, усталость, и производительность начинает убывать.
Рис. 25. Производительность деятельности агента
Рис. 24. Зависимость результата (кумулятивного) деятельности агента от времени
В многочисленных исследованиях (проведенных в основном в доперестроечный период) отечественных ученых [2, 7, 27, 77] также встречаются кривые (зависимости производительности труда от времени в течение рабочего дня) типа приведенных на рисунке 25. Эскиз графика характерной зависимости производительности труда рабочих (с учетом перерыва на обед) от времени изображен на рисунке 26 (нулевой момент времени соответствует началу рабочего дня; во время обеденного перерыва - на интервале [т; Т2] - производительность равна нулю; момент времени Т3 соответствует окончанию рабочего дня).
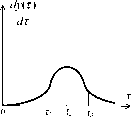
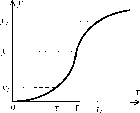
Содержательные интерпретации участков возрастания, постоянства и убывания производительности труда очевидны.
Нелинейное изменение результата деятельности агента во времени позволяет выделить два типа агентов [101], которых следует оплачивать по-разному. Поясним последнее утверждение.
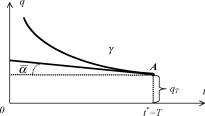
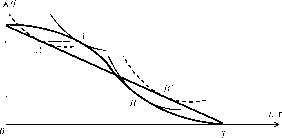
Если принять, что функция затрат агента имеет вид, изображенный на рисунке 24, то при использовании центром компенсаторной системы стимулирования кривые безразличия агента могут касаться кривой бюджетного ограничения в одной из двух характерных точек - точке А, в которой кривая бюджетного ограничения вогнута (первый тип), или в точке В, в которой кривая бюджетного ограничения выпукла (второй тип - см. рисунок 27).
Рис. 27. Два типа агентов
Если цель центра заключается в том, чтобы при минимальном вознаграждении агента побуждать его к увеличении продолжительности рабочего времени, то для агентов первого типа следует использовать повременную систему (пропорциональную, в которой показателем является продолжительность рабочего дня) стимулирования, а для агентов второго типа - сдельную (компенсаторную, в которой показателем является результат деятельности) - см. горизонтальные прямые и точки А, А’ и В, В’ на рисунке 27.
Системы стимулирования D-типа. Напомним, что в системах стимулирования, основанных на перераспределении дохода, вознаграждение агента пропорционально (с коэффициентом пропорциональности не зависящим от действия агента) доходу центра H(y), который зависит от действия агента, то есть oD(t) = XH(t),
X € [0; 1].
Если функция дохода центра вогнутая (что обычно предполагается как в теоретико-игровых, так и в экономических моделях [39, 41, 43]), то функции oD(t) и ~D (t) также являются вогнутыми. На рисунке 28 изображены функции стимулирования Od(t) и Sd (t), а также кривая безразличия, соответствующая максимальному значению полезности агента (эта кривая касается кривой ~D (t) в точке А).
Рис. 29. Функция стимулирования D-типа
Вогнутые функции стимулирования.
Пусть функция стимулирования (бюджетное ограничение) вогнутая, а кривая безразличия агента - выпуклая (см. рисунок 29). Тогда для данной системы стимулирования можно произвести линеаризацию (см. выше), то есть найти систему стимулирования L+C-типа, реализующую то же действие, что и исходная система стимулирования.
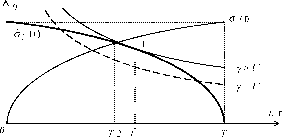
Величина qT называется нетрудовым доходом (она равна доходу агента при нулевом рабочем времени).
Рис. 29. Линеаризация вогнутой функции стимулирования
Итак, мы рассмотрели описание основных базовых систем стимулирования в терминах экономики труда. Используя полученные результаты, легко получить аналогичные описания для остальных базовых систем стимулирования.
Проиллюстрируем возможность переноса на примере составных и суммарных систем стимулирования.
Системы стимулирования LL-типа (составные). Напомним, что составной системой стимулирования LL-типа называется такая система стимулирования, в которой агент поощряется пропорционально действию, причем на различных участках множества возможных действий A = [0; T] коэффициенты пропорциональности О1 и а2 различны. Так как выше было показано, что оптимальная система стимулирования должна быть возрастающей и выпуклой, то рассмотрим случай, когда 0 о1 ? О2 (при о1 = О2 получим подробно рассмотренную выше систему стимулирования L-типа). Условием оптимальности является равенство ставки оплаты и альтернативной стоимости одного часа досуга.
Следовательно, возможны три варианта - кривая безразличия полезности агента касается бюджетной кривой, имеющей вид ломаной, либо на линейном участке с углом наклона а (точка А - см. рисунок 30), либо на линейном участке с углом наклона а2 (точка В - см. рисунок 31), либо на обоих участках сразу (точки А и В - см. рисунок 32) - см. также описание систем стимулирования LL-типа в разделе 1.3.
Рис. 30.
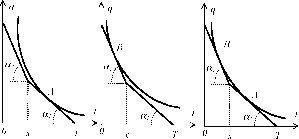
Рис. 31.
Рис. 32.
Система стимулирования LL-типа
Системы стимулирования L+C-типа (суммарные). Напомним, что суммарной системой стимулирования L+С-типа называется такая система стимулирования, при использовании которой агент поощряется пропорционально действию, причем, если его действие (количество отработанных часов) превышает норматив х, то ему доплачивается постоянная величина C. Как и ранее, возможны три варианта - кривая безразличия полезности агента касается бюджетной кривой, имеющей вид разрывной прямой, на линейном участке с углом наклона а либо правее точки х (точка А - см. рисунок 33), либо левее этой точки (точка В - см. рисунок 34), либо, что не исключено в силу выпуклости кривых безразличия, одновременно в точке х и правее ее (точки А и В - см. рисунок 35).
Рис. 33.
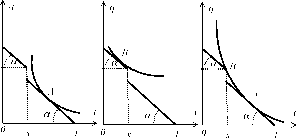
Рис. 34.
Рис. 35.
Система стимулирования L+С-типа
Итак, мы рассмотрели взаимосвязь между теоретико-игровыми моделями стимулирования и экономическими моделями предложения труда. Проведенный анализ позволил не только провести содержательные аналогии, но и установить количественные соотношения между параметрами этих двух классов моделей.
В контексте настоящего исследования важный качественный вывод, который можно сделать - это то, что изучение моделей индивидуального поведения на рынке труда (точнее говоря - выявление зависимости желательной продолжительности рабочего времени от ставки оплаты и определение на основе этой информации свойств функции полезности [50, 103, 105, 106, 118, 123]) позволяет использовать функцию затрат, которая является существенной компонентой теоретико-игровой модели. Значит, для того, чтобы найти функцию затрат, необходимо знать функцию индивидуальной полезности или более частные зависимости, определяющие поведение агента на рынке труда, что выдвигает конструктивные требования к процедуре идентификации [56, 91, 95] систем стимулирования в реальных организационных системах [47, 50].
МЕХАНИЗМЫ ФОРМИРОВАНИЯ ФОНДА ЗАРАБОТНОЙ ПЛАТЫ
В модели индивидуального стимулирования, рассмотренной в первой части настоящей работы, предпочтения участников организационной системы описывались их целевыми функциями. Целевая функция центра фо, у) представляла собой разность между его доходом H(y) от деятельности агента у е A, принадлежащего допустимому множеству A, и стимулированием о(у), о(-) е M, принадлежащим допустимому множеству M, то есть:
F(S у) = H(y) - Sy).
Целевая функция агента fs, у) являлась разностью между его доходом - стимулированием, то есть вознаграждением, выплачиваемым ему центром, и затратами c(y):
As у) = Sy) - c(y).
Таким образом, при рассмотрении задач стимулирования модель организационной системы задается предпочтениями участников в отсутствии стимулирования и допустимыми множествами: S = [H(-), c(-), M, A}. При описании той или иной реальной организационной системы множества допустимых стратегий (функций стимулирования и действий агента), как правило идентифицируются достаточно просто.
Если деятельность агента оценивается такими показателями как отработанное время, объем выпуска, объем реализованных товаров и т.д., то множество его возможных действий определяется множеством тех значений показателей, которые являются допустимыми с точки зрения физических и технологических ограничений. Понятно, что, например, отработанное время не может быть отрицательным, объем реализованных товаров не может превышать их количество, имеющееся на складе, и т.д.
Ограничения на стимулирование (класс допустимых систем стимулирования) в каждом конкретном случае также определяются достаточно просто. Как правило, они заданы экзогенно, то есть фиксированы, или связаны с функцией дохода центра - см. более подробно ниже. При этом целесообразно различать (иногда услов-
но) два типа ограничений на стимулирование. Первый тип - ограничения на абсолютную величину вознаграждения агента. Например, из неотрицательности целевой функции центра (из условия индивидуальной рациональности) следует, что при данном действии агента величина его вознаграждения не должна превышать доход центра от этого действия.
Второй тип - ограничения на свойства зависимости вознаграждения агента от его действия. Второму типу ограничений соответствует, например, требование использования одного из классов базовых систем стимулирования -пропорциональных (повременных, сдельных и др. с фиксированными ставками оплаты), скачкообразных (аккордных, премиальных и др.) и т.д.
