ЭФФЕКТИВНОСТЬ БАЗОВЫХ СИСТЕМ СТИМУЛИРОВАНИЯ
Как и системы оплаты, используемые в России, так и такие системы оплаты, используемые за рубежом, как: система двух ставок, система контролируемой дневной выработки, надбавки за квалификацию, плата за знание и компетенцию, системы Тейлора, Скэнлона, Роуэна, Барта, Гантта, Меррика, эмпирические системы и др. (см. подробности в [17, 20, 35 и др.]), также могут быть формально описаны соответствующей базовой системой стимулирования.
Таким образом, краткий обзор основных используемых на практике систем оплаты труда позволяет сделать вывод, что подавляющее большинство из них охватывается множеством введенных выше моделей базовых систем стимулирования. При этом можно утверждать, что такие формы индивидуальной заработной платы как: повременная, сдельная, участие в доходе, премиальная (и соответствующие им системы оплаты: простая повременная, повременно-премиальная, прямая сдельная, сдельно-премиальная, сдельно-прогрессивная, косвенно-сдельная и аккордная и др.) могут быть относительно адекватно описаны следующим множеством систем стимулирования (см. их определения выше): L, LL, L+C или LL+C, D, C.
Установив в первом приближении качественную взаимосвязь теоретических моделей систем стимулирования с формами индивидуальной заработной платы, перейдем к изучению сравнительной эффективности тех или иных простых базовых систем стимулирования в одноэлементных детерминированных
организационных системах.
ГЛАВА 3. ЭФФЕКТИВНОСТЬ БАЗОВЫХ СИСТЕМ СТИМУЛИРОВАНИЯ
Рассмотрим перечисленные выше базовые системы стимулирования, акцентируя в основном внимание на их эффективности (то есть на минимальных затратах на стимулирование по реализации ими тех или иных действий агента - см. раздел 1.2). Параллельно с теоретическим исследованием будем рассматривать иллюстративный пример - модель стимулирования в одноэлементной детерминированной ОС, в которой функция дохода центра равна: H(y) = by, b 0, а функция затрат агента равна: c(y) = ay, a 0.
Если не оговорено особо, будем считать выполненными предположения А.1, А.2, А.3 и А.4.
Так как выше было доказано, что компенсаторные (и квазикомпенсаторные) системы стимулирования оптимальны, то есть обладают максимальной эффективностью, то необходимо сравнить эффективность других базовых систем стимулирования с эффективностью квазикомпенсаторных.
Скачкообразные системы стимулирования (С-типа).
Как отмечалось выше, если не наложено ограничений на абсолютную величину индивидуального поощрения (предположение
А.3), то при исследовании скачкообразных систем стимулирования амплитуду скачка C (то есть величину вознаграждения в случае выполнения плана) следует считать переменной величиной, устанавливаемой центром, наряду с планом.
Множество действий, реализуемых системами стимулирования С-типа, имеет вид P(C) = {y е A | c(y) ? С }. В том числе, в рамках предположения А.3' Р(С) = [0; у+(С)], где c(y+) = С. Минимальные затраты на стимулирование равны: sminC(y) = C, у е P(C). Следовательно, у е P(C) выполнено (1) D(C;K) = C - c(y) 0.
При использовании квазискачкообразных систем стимулирования оценка (1) также остается в силе.
Таким образом, скачкообразные системы стимулирования имеют эффективность, не превышающую эффективность компенсаторных, и совпадающую с последней при реализации действий, лежащих на границе множества реализуемых действий, определяемой ограничениями механизма стимулирования.
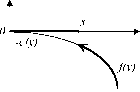
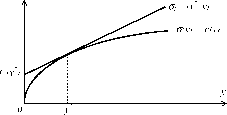
График целевой функции агента при использовании центром системы стимулирования sC(x,y) (при некотором x е P(C)) приведен на рисунке 13 (отметим, что для наглядности в рисунках настоящего подраздела функция затрат агента изображается с обратным знаком).
Рис. 13. Целевая функция агента при использовании центром системы стимулирования С-типа
Если ограничение C фиксировано, то при монотонной функции дохода центра оптимальным является реализация максималь-
ного действия y+(C), при этом ami„c(y+(C)) = ami„eK(y+(C)). В рассматриваемом примере у ' = VC7 a .
Отметим также, что при оптимальном подборе центром соответствующих параметров системы стимулирования СС-типа и С+С-типа эквивалентны некоторой базовой системе стимулирования С-типа, поэтому подробно рассматривать первые две из них не имеет смысла.
Компенсаторные системы стимулирования (K-типа).
При использовании компенсаторных (или квазикомпенсатор-ных) систем стимулирования минимальные затраты на стимулирование равны затратам агента.
Итак: 7ті„к(у) = c(y), у е P(C). Очевидно, D(K; K) = 0. В рассматриваемом примере: в рамках предположения А.3 выполнено: у* = arg max {by-ay2} = b/2a, то есть Кк = Ф(у*) = b2/4a; в рамках
у 0
предположения А.3': KqK = max {Ф(у*), Ф(у+(С)}, где
Ф(у+(С) = b^C / a - C, причем, если максимум целевой функции центра достигается в точке y+(C) (используется весь размах функции стимулирования), то оптимальными являются также и скачкообразные системы стимулирования с ограничением C.
График целевой функции агента при использовании центром системы стимулирования oK(x,y) (при некотором x е P(C)) приведен на рисунке 14.
Рис. 14. Целевая функция агента при использовании центром системы стимулирования K-типа
Пропорциональные системы стимулирования (L-типа).
При использовании пропорциональных (линейных) или квазилинейных систем стимулирования и непрерывно дифференцируе-52
мой монотонной выпуклой функции затрат агента выбираемое им действие определяется следующим выражением: y = c (a), где
c' 1 (- ) - функция, обратная производной функции затрат агента. При этом величина
(2) D(L, K) = Ominb(y*) - тіпк(у*) = У* c'(y*) - c(y*) всегда (при любых a 0, и, следовательно, при любых у 0) неотрицательна. В рассматриваемом примере sminL(y*) = 2(у*)2, то есть у* е A' Omirdy) / SminK(y*) = 2.
Таким образом, при выпуклых функциях затрат агента эффективность пропорциональных систем стимулирования не выше, чем компенсаторных. График целевой функции агента при использовании центром пропорциональной системы стимулирования приведен на рисунке 15.
0
Рис. 15. Целевая функция агента при использовании центром системы стимулирования L-типа
Если функция затрат агента вогнутая, то для любой компенсаторной системы стимулирования выполнено: о(у) = c(y), и для любого действия, выбираемого агентом, существует система стимулирования L+C типа (зависящая от действия агента) не меньшей эффективности (см. рисунок 16).
Действительно, пусть агент при использовании компенсаторной системы стимулирования выбирает действие у . Система стимулирования L+С-типа со следующими параметрами: x = 0, C(y*) = c(y*) - c’(y*) у*, a(y*) = c (у*), реализует действие у* с теми же затратами на стимулирование, что и исходная компенсаторная система стимулирования (см. рисунок 16).
Описанный выше прием перехода от вогнутой компенсаторной к пропорциональной системе стимулирования называется линеаризацией системы стимулирования.
Рис. 16. Линеаризация вогнутой функции стимулирования
Системы стимулирования,
основанные на перераспределении дохода (D-типа).
В работах [69, 71-73] при достаточно общих предположениях показано, что использование систем стимулирования, основанных на перераспределении дохода, неэффективно (в сравнении с компенсаторными системами стимулирования).
Другими словами, y е A величина
(^) D(D, K) SminD(y ) " SminQK(y )
всегда неотрицательна. В рассматриваемом примере, так как функция дохода центра линейна по действию агента, то перераспределение дохода эквивалентно использованию пропорциональных систем стимулирования - при этом ставка оплаты a = X b, то есть: SminD^y *) = Отть(у) = 2(y*)2, X(y*) = 2ay*/b, следовательно y* ?b/2a.
Эффективность системы стимулирования D-типа может быть и в точности такой же, как и эффективность абсолютно оптимальной квазикомпенсаторной системы стимулирования. Для этого достаточно, например, однотипности функции затрат агента и функции дохода центра.
Если в рассматриваемом примере H(y) = by2, где b а, то KD = KqK (правда, если а b, то системами стимулирования D-типа нельзя реализовать никаких действий, кроме нулевого).
Системы стимулирования LL-типа.
При использовании центром систем стимулирования LL-типа целевая функция агента имеет вид:
(4) я=ay - c( y)’ y ? г,
[а2y + (1 - 2)x - c(y), y ^ x
где x - величина действия, при превышении которого увеличивается ставка оплаты (см. рисунок 11).
Пусть функция затрат агента удовлетворяет предположениям
А.1, А.2'' и А.3. Обозначим yj = c'~X (аІ), y2 = c'~l (а2). Отметим, что в рамках введенных предположений эти точки существуют и единственны, кроме того всегда выполнено: y^ ? y2, x ? y2 Возможны следующие случаи:
1. yj ? x ?y2, f( yl) f( y2) (в рассматриваемом примере этому соответствует выполнение а1 + а2 ? 4ax), тогда агент выбе-
2
рет действие Уі , то есть второй кусок (со ставкой а2) функции стимулирования не работает, при этом система стимулирования эквивалентна пропорциональной;
2. yj ? x ?y2, f( y1 ) ?f( yj) (в рассматриваемом примере этому соответствует выполнение а1 + а2 4ax), тогда агент выбе-
2
рет действие У2, то есть первый кусок (со ставкой а2) функции стимулирования не работает, но при этом система стимулирования не эквивалентна пропорциональной (см. оценку минимальных затрат на стимулирование ниже);
22
3. y1 ? y2 ? x, то есть получаем, практически, первый случай.
4. x ? yl ? y2, f( y1 ) ? f( y2), то есть получаем, практически, второй случай.
Итак, интерес представляют (из-за отличия от систем L-типа) второй и четвертый из описанных выше случаев. Очевидно, 22
sminLL( У2) ? sminL( У2). Для рассматриваемого примера имеет место:
(^) SminL( у2) SminLL( У2) (а2' а1) x.
Из выражения (5) видно, что эффективность системы стиму-
*
лирования LL-типа возрастает с ростом параметра x У2. Если
отсутствуют ограничения на ставки оплаты, то получаем, что при
*
а1 = 0 при стремлении x к у2 система стимулирования LL-типа стремится к системе стимулирования С-типа со скачком в точке x.
Содержательно, максимально эффективной является неоплата (оплата с нулевой ставкой) действий, меньших плана, и компенсация затрат при точном выполнении (и/или перевыполнении плана) или пропорциональная оплата со ставкой, равной предельным затратам агента в точке плана.
Качественно, более высокую по сравнении с системами стимулирования L-типа эффективность систем LL-типа с последовательно возрастающими ставками оплаты можно объяснить тем, что последние ближе (точнее аппроксимируют) к выпуклой функции затрат агента. Кусочно-линейные системы стимулирования LLL-типа, LLLL-типа и т.д. с последовательно возрастающими ставками оплаты будут еще точнее аппроксимировать возрастающую выпуклую функцию затрат агента и, следовательно, будут иметь еще более высокую эффективность, приближаясь (по мере увеличения числа составляющих) к эффективности компенсаторной системы стимулирования.
Системы стимулирования СС-типа и С+С-типа, очевидно, эквивалентны (имеют ту же эффективность и те же минимальные затраты на стимулирование) базовым скачкообразным системам стимулирования (с одним скачком), поэтому подробно рассматривать их мы не будем.
Системы стимулирования L+C-типа и LL+С-типа.
Пусть функция затрат агента удовлетворяет предположениям
А.1-А.3 и c'(0)=0. Обозначим у1 = е'~х (а1), у2 = с,_1(а2) (см. также системы стимулирования LL-типа). Система стимулирования LL+C-типа в зависимости от соотношения параметров может
**
реализовывать одно трех из действий: уі , x или у ^, где x - точка скачка.
По аналогии с исследованием систем LL-типа, для этого класса систем стимулирования можно показать, что их эффективность не ниже, чем эффективность систем L-типа и, естественно, не выше, чем систем K-типа и C-типа.
Системы стимулирования C+D-типа.
Содержательно, при использовании систем стимулирования C+D-типа индивидуальное вознаграждение агента складывается из оклада (выплачиваемого при условии выполнения, например, должностных обязанностей - тарифная система оплаты труда) и компоненты, зависящей от результатов деятельности всей организационной системы, точнее говоря - дохода центра, выражающего интересы системы в целом.
Обозначим с (X, y) = c(y) - X H(y). Тогда целевая функция агента может быть записана в виде:
(6) AX, y) = Sy) - с (X, у).
Произведя замену переменных (затрат), мы получили параметрическую (параметр - %) задачу синтеза оптимальной скачкообразной системы стимулирования в ОС с целевой функцией агента, определяемой (6), методы решения которой детально исследованы (см. [71, 72 и др.]). Таким образом, задача поиска оптимальной системы стимулирования C+D-типа решается в два этапа. На первом этапе для фиксированного X ищется оптимальная система стимулирования С-типа.
На втором этапе ищется оптимальное значение параметра X е [0; 1].
Системы стимулирования K+A-типа и C+A-типа.
Относительно суммарных систем стимулирования следует сделать следующее общее замечание. Пусть A и B - классы компонент (слагаемых) некоторой суммарной системы стимулирования из класса A+B.
Условие реализуемости действияy е A'имеет вид: y е A' Oa+бІУ*) - c(y*) Оа+б(у) - c(y).
При этом минимальные затраты на стимулирование по реализации действия у равны
(7) Omm(A+B)(y*) = Оліу*) + oBy).
Свойство аддитивности минимальных затрат на стимулирование, отражаемое выражением (7), позволяет сделать важный вывод о свойстве суммарных систем стимулирования, в которых одной из компонент является компенсаторная или оптимальная (см. выше) скачкообразная системы стимулирования. Так как одна из компонент (оптимальная С-типа или К-типа) системы стимулирования C+A-типа или K+A-типа компенсирует затраты агента по выбору некоторого действия, то компонента А является лишней с точки зрения реализуемости этого действия, играя роль дополнительной мотивации (см. также ниже). Из вышесказанного и (7) следует, что справедлива следующая оценка: у е A
(8) D(K+A, K) = D(C+A, C) = OA(y').
Выражение (8) дает возможность легко оценить экономические потери от использования систем стимулирования C+A-типа или K+A-типа по сравнению с системами стимулирования С-типа или К-типа.
Содержательно (8) означает, что агент выбирает действие, при котором достигается максимум дополнительного (с учетом полностью компенсированных его затрат) вознаграждения sA(y). Поэтому анализ систем стимулирования C+A-типа или K+A-типа вырождается и заключается в поиске системы стимулирования А, которая будет: 1) иметь максимум в точке, которую хочет реализовать центр; 2) обладать достаточным мотивирующим эффектом; 3) иметь в точке максимума минимальное значение (с учетом второго пункта требований).
Итак, мы рассмотрели основные свойства базовых систем стимулирования: скачкообразных, компенсаторных, пропорциональных и основанных на перераспределении дохода и ряда производных от них систем стимулирования. Сводка полученных выше оценок их сравнительной эффективности (оценок затрат на стимулирование при любых допустимых действиях агента) приведена в таблице 1.
Знак (), стоящий на пересечении некоторой строки и столбца таблицы 1, означает, что в рамках введенных предположений при использовании системы стимулирования, соответствующей строке, эффективность всегда не меньше (не больше) а, следовательно, минимальные затраты на стимулирование не больше (не меньше), чем при использовании системы стимулирования, соответствующей столбцу. Знак ? означает, что соотношение затрат на стимулирование зависит от конкретного случая - параметров организационной системы, то есть свойств целевых функций и допустимых множеств и т.д. - и требует дополнительного исследования в каждом из этих конкретных случаев.
Утверждение 5. Если выполнены предположения А.1-А.4, то сравнительные эффективности базовых систем стимулирования удовлетворяют соотношениям, приведенным в таблице 1.
Выше были выделены четыре основных, двенадцать суммарных и пятнадцать составных (двойных), то есть всего 31 простая базовая система стимулирования. Мы исследовали (в рамках предположений А.1-А.3 о свойствах параметров модели организационной системы) с той или иной степенью детализации некоторые (K, C, L, D, LL, L+С и др.) из базовых систем стимулирования, отражающих наиболее часто используемые на практике системы индивидуальной заработной платы.
Полное исследование сравнительной эффективности всех базовых систем стимулирование подразумевает, как минимум, попарное сравнение соответствующих минимальных затрат на стимулирование, результатами которого могла бы стать таблица типа таблицы 1, имеющая 31 X 31 = 961 ячейку. Заполнение такой таблицы является трудоемкой, но, в принципе, реализуемой задачей.
В то же время, такое детальное исследование всех возможных комбинаций представляется нецелесообразным по следующим причинам.
Во-первых, выше при описании результатов исследования комбинаций, вошедших в таблицу 1, мы зачастую вводили те или иные предположения как относительно свойств целевых функций, так и относительно соотношений конкретных параметров, явно оговаривая или неявно подразумевая (будучи обоснованно уверенными [69, 70, 72]), что небольшие изменения этих параметров не повлияют на сделанные выводы и, в частности - на оценки сравнительной эффективности.
Во-вторых, из приведенных результатов видно, что техника анализа различных комбинаций практически одинакова (что и является одной из основ упомянутой выше уверенности): следует вычислить действия, реализуемые используемой системой стимулирования, определить минимальные затраты на стимулирование и сравнить их с соответствующими показателями для других базовых систем стимулирования.
Таким образом, с одной стороны, учет всего многообразия возможных вариантов достаточно трудоемок, с другой стороны единообразие, простота и алгоритмичность их анализа свидетельствуют о наличии единых (методологических и методических) подходов к их изучению. Поэтому, наверное, нецелесообразно исследовать все комбинации моделей, а лучше предоставить исследователю операций возможность самостоятельно реализовать в каждом конкретном случае единый подход к изучению как существующих на практике систем оплаты, так и их формальных моделей.
Существенными для проведенного анализа являлись введенные выше предположения о поведении агента - в частности: используемых им принципах рационального выбора, свойствах функции затрат и т.д. Поэтому перспективным направлением дальнейших исследований представляется ослабление этих предположений, то есть расширение множества моделей и исследование возможности использования предложенного выше подхода (анализ минимальных затрат на стимулирование) в этом более широком их классе.
Кроме того, необходимо установить связь между теорией и практикой, указав откуда берутся те или иные параметры, фигурирующие в теоретико-игровых моделях стимулирования в организационных системах. Эта задача решается в последующих частях настоящей работы.
Более конкретно - во второй части рассматривается взаимосвязь между теоретико-игровыми моделями стимулирования и моделями экономики труда; третья часть посвящена обсуждению проблем идентификации функции дохода центра, то есть экономических механизмов формирования фонда заработной платы.
ЭКОНОМИКА ТРУДА И ТЕОРЕТИКО-ИГРОВЫЕ МОДЕЛИ
Экономика труда - раздел экономической теории, изучающий функционирование рынка в сфере труда, то есть поведение работодателей и работников в ответ на действие общих факторов: заработной платы, цен, условий труда и т.д. В контексте исследования базовых систем стимулирования нас будет интересовать индивидуальное поведение на рынке труда (точнее те его составляющие, которые определяются действующими на этом рынке механизмами и системами стимулирования), то есть принципы принятия решений агентом, являющимся субъектом рынка труда.
В рамках моделей, использующихся в экономике труда [53, 88, 96, 113, 119, 132, 134], параметры рыночного равновесия определяются спросом и предложением (балансом спроса и предложения рабочей силы). Так как мы изучаем поведение отдельного агента, то ограничимся рассмотрением моделей предложения труда.
Сделав маленькое отступление, отметим, что использование условия равенства спроса и предложения рабочей силы позволяет определить рыночную заработную плату. В то же время, для фиксированных предприятия и работника существует эффективная заработная плата (см. определение выше), которая соответствует максимизации прибыли предприятия (при этом оптимальное действие агента определяется из условия равенства его предельной производительности и предельных затрат). Так как в определении эффективной заработной платы фигурирует рыночная переменная, соответствующая ограничению пособия по безработице (или, что то же самое, ограничению резервной заработной платы), то эффективная заработная плата не ниже рыночной.
Подчеркнув это различие, напомним, что в настоящей работе мы исследуем модель взаимодействия агента и центра (соответственно, работника и предприятия), то есть в основном рассматривается именно эффективная, а не рыночная заработная плата.
Прерогативой агента - стороны, предлагающей рабочую силу на рынке труда является, в частности, определение (совместно с работодателем - см. подробности в [96]) продолжительности рабочего времени, понимаемой в широком смысле - и как продолжительность рабочего дня, и как возможную работу в течение неполного рабочего дня и т.д. Для простоты будем считать, что единственной альтернативой рабочему времени является время, затрачиваемое на досуг, поэтому предложение труда эквивалентно спросу на досуг [98, 129, 133, 135].
Опять же для упрощения изложения, пока не будет оговорено особо, будем считать, что совокупный доход пропорционален количеству отработанных часов, то есть предположим, что на рынке труда используются только пропорциональные (повременные) системы стимулирования, в которых ставка оплаты постоянна и не зависит от суммарного количества отработанных часов.
В рамках введенных предположений в равновесии для агента альтернативные издержки одного часа досуга равны ставке заработной платы (и наоборот) - тому дополнительному заработку, который мог бы быть получен при работе в течении этого часа.
Проанализируем поведение агента на рынке труда, то есть исследуем его предпочтения в дилемме труд - досуг, в рамках которой характеристикой предложения труда является желаемая продолжительность рабочего времени. Анализ будем проводить последовательно усложняя описание модели поведения - от качественного вербального обсуждения к графическому анализу и, наконец, к формальной математической модели.
В экономике труда считается, что индивидуальное поведение на рынке рабочей силы определяется двумя эффектами - дохода и замещения.
Эффект дохода заключается в том, что с увеличением совокупного дохода снижается желаемая продолжительность рабочего времени. Соответственно, если целью агента является поддержание совокупного дохода постоянным, то увеличение ставки оплаты в рамках эффекта дохода приведет к сокращению желаемой продолжительности рабочего времени, и наоборот - для поддержания дохода постоянным при сокращении ставки оплаты желаемая продолжительность рабочего времени возрастет.
Примером проявления чистого эффекта дохода является получение наследства [96].
Эффект замещения заключается в том, что увеличение ставки оплаты приводит к увеличению желаемой продолжительности рабочего времени - альтернативная стоимость одного часа досуга возрастает и агент предпочтет отработать большее количество часов.
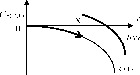
Таким образом, если доминирует эффект дохода, то агент реагирует на повышение ставки заработной платы сокращением предложения труда, а если доминирует эффект замещения, предложение труда увеличивается (см. рисунок 17). Изображенная на рисунке 17 кривая зависимости желательной продолжительности рабочего времени t от ставки оплаты а получила название кривой обратного изгиба [96].
Пусть полезность агента u(q, t) зависит от его дохода q е Ш1 и продолжительности ежедневного свободного времени t е [0; T], где свободное и рабочее время связаны условием t + t = T.
