Функция дохода центра и функция затрат агента
Сложнее дело обстоит с определением таких компонентов модели организационной системы как функция дохода центра и функция затрат агента. Последняя может идентифицироваться в рамках экспериментального исследования предпочтения агентов, выполняемого в рамках методологии, описанной во второй части настоящей работы, объединяющий теоретико-игровые модели и модели экономики труда.
Поэтому перейдем к подробному обсуждению функции дохода центра.
В данной части настоящей работы предполагается (там где это необходимо), что функция затрат единственного агента известна, и основной акцент делается на исследование взаимосвязи между функцией дохода центра и основными экономическими и финансовыми показателями деятельности организации, интересы которой отражает центр.
Другими словами, мы попытаемся ответить на вопрос о том как по известным, например, из финансовой отчетности организации показателям ее деятельности определить функцию дохода, которая может быть использована в теоретико-игровой модели для синтеза оптимальной системы стимулирования.
Традиционно системы оплаты труда делятся на тарифные и бестарифные [19, 20, 35]. И в тех, и в других системах оплаты фигурируют определенные параметры, коэффициенты, нормативы и т.д., однозначно определяющие вознаграждение агента данной квалификации, выполняющего данную работу в данных условиях.
В тарифных системах оплаты такими коэффициентами являются тарифные ставки, нормы трудозатрат и др., в бестарифных
системах - коэффициенты квалификационного уровня, трудового участия, параметры, определяющие вилки окладов, и др. В государственных организациях (в целях унификации, если не требуется делать различий, под организацией или ОС здесь и далее мы будем понимать предприятия, фирмы, организации, ведомства и т.д.) эти параметры системы оплаты труда регулируются законодательно (примерами могут служить единая тарифная сетка, различные тарифно-квалификационные нормативы и т.д.).
В негосударственных организациях наиболее распространена практика, когда непротиворечащие (а иногда и противоречащие) законодательству условия оплаты труда устанавливаются руководством организации, причем далеко не всегда эти условия обоснованы и увязаны с результатами экономической деятельности организации.
Следовательно, при заданном составе агентов и фиксированном классе допустимых систем стимулирования возникает задача определения оптимальных значений параметров зависимости вознаграждения от действий агентов. Так как параметры системы стимулирования определяют действия, выбираемые агентами, а последние, наряду с величинами вознаграждений, приводят к определенным результатам деятельности организационной системы в целом, то для решения этой задачи необходимо установить взаимосвязь между действиями агентов и их вознаграждениями с одной стороны, и результатами деятельности системы с другой стороны.
В первом приближении можно выделить два подхода к описанию взаимосвязи между параметрами системы стимулирования и результатами деятельности организации . Так как конечной целью (критерием оптимизации) является увеличение (или уменьшение) значений основных показателей деятельности организации, то оба подхода имеют много общего. Различия между ними обусловлены тем, какие факторы - действия агентов или результат деятельности организации - выбираются за основу рассмотрения.
Первый подход - снизу - вверх - заключается в том, что для заданной системы оплаты определяются действия, которые выбираются агентами при ее использовании, и те затраты на стимулирование (ФЗП), которые несет при этом центр. Действия агентов и ФЗП входят в основные показатели деятельности организации, поэтому, варьируя систему стимулирования, можно генерировать различные варианты значений этих показателей, и затем выбирать ту систему стимулирования, на которой достигаются наилучшие значения показателей. Методики вычисления индивидуальных вознаграждений агентов, фондов оплаты труда подразделений и организации в целом для различных систем оплаты подробно рассмотрены в литературе (см., например, работы [23, 37, 52, 92]), поэтому останавливаться на них мы не будем.
Одним из основных недостатков подхода снизу-вверх является слабая взаимосвязь между вознаграждением конкретного агента и результатами деятельности организации.
Второй подход - сверху - вниз (иногда его называют остаточным принципом) - к описанию взаимосвязи между параметрами системы стимулирования и результатами деятельности организации заключается в следующем. В показателях деятельности организации в целом, в том числе - зависящих от результатов деятельности (действий) агентов, выделяются составляющие, зависящие от фонда оплаты труда.
Затем, с учетом интересов и предпочтений агентов (собственно задача стимулирования в терминологии, которой следует настоящая работа - см. первую часть) определяется система оплаты труда (и, следовательно, действия агентов), которая приводит к наилучшим значениям показателей деятельности организации.
Второй подход в большей степени, чем первый, учитывает результаты деятельности организации, однако при его использовании возникают трудности, связанные с необходимостью корректного учета специфики конкретной организации, для которой он применяется, поэтому рассмотрим остаточный принцип более подробно.
В политике заработной платы важное место занимает выбранный метод формирования средств на оплату труда агентов, участвующих в деятельности организации. Методы формирования фонда заработной платы (ФЗП) прямо или косвенно влияют на показатели деятельности организации в целом, а те в свою очередь - на фактическую величину вознаграждения, то есть - заработной платы, премий, доплат, надбавок и т.д.
Перечислим кратко некоторые методы формирования фонда заработной платы.
Уровневый метод. При использовании уровневого метода ФЗП определяется в процентах к объему производства (по себестоимости). Применяемый первоначально (в бывшей социалистической экономике СССР) для автотранспортных и строительных предприятий, этот метод постепенно распространился на ряд предприятий других отраслей. Если процент (доля заработной платы) фиксирован, то объем производства однозначно определяет величину ФЗП.
Данный метод может рассматриваться как основанный на использовании систем стимулирования D-типа, следовательно, он обладает всеми недостатками, присущими этому классу систем стимулирования - см. главу 3 и [69, 71, 73]. Его преимуществом является ярко выраженная направленность на мотивацию увеличения объема производства, которая должна соотноситься с соответствующими затратами агентов, что устанавливает границы эффективности применения уровневого метода.
Нормативно-приростной метод. При использовании нормативно-приростного метода рост ФЗП относительно существующего базового уровня производится в расчете на один процент увеличения объема производства.
Недостатком данного метода является стимулирование роста количественных показателей, но не качества и, тем более, не экономии ресурсов.
И уровневый, и нормативно-приростной метод связаны с предварительным расчетом ожидаемой в плановом периоде доли заработной платы в общем объеме того или иного базового показателя (оценки объема продукции или ее прироста). Более того, их общим существенным недостатком является то, что процент, который составляет (или на который увеличивается) ФЗП не зависит от абсолютной величины базового показателя.
Наверное, более эффективным оказалось бы использование гибких нормативов, то есть нормативов, зависящих от абсолютной величины базового показателя. Однако, на сегодняшний день они не нашли достаточного распространения на практике.
Остаточный метод. Как отмечалось выше, при использовании остаточного метода (принципа) ФЗП выступает составной частью более общего показателя хозяйственно-финансовой деятельности организации, например - хозрасчетного коммерческого дохода, включающего также и прибыль.
Вся сложность оценки достоинств и преимуществ остаточного метода заключается в том, что каких-либо относительно общих научно обоснованных размеров доли (в абсолютных или относительных единицах), например, валового дохода, оставляемого на оплату труда, на сегодняшний день не существует. Несомненно, что эта доля не может быть меньше, чем произведение минимальной ставки оплаты труда на численность работников, и больше, чем валовой доход.
Не вводя дополнительных предположений, сказать что-либо более конкретное нельзя, поэтому рассмотрим остаточный метод более подробно.
Финансовая модель организации. Для того чтобы привести какие-либо рекомендации относительно использования остаточного метода формирования ФЗП необходимо рассмотреть взаимосвязь между основными показателями финансово-хозяйственной деятельности организации, то есть построить ее финансовую модель.
Для простоты рассмотрим организацию, состоящую из центра и одного агента и описываемую следующими основными показателями финансово-хозяйственной деятельности:
- действие агента y е A, которое (как и выше) может интерпретироваться как отработанное время, объем выпущенной продукции или оказанных услуг и т.д.;
- с0 0 - постоянные издержки организации (центра), включая амортизационные отчисления, коммерческие и др. расходы;
- c0(y) 0 - переменные издержки организации, включая, материальные затраты и т.д.;
- W(y) - доход организации, зависящий от действий агента (например, выручка от реализации);
- V(y) - валовая прибыль;
- рі - ставка налога с прибыли;
- P(y) - чистая прибыль;
- S(y) - себестоимость;
- o(y) - вознаграждение агента;
- с(у) - затраты агента;
- р2 - суммарные начисления на оплату труда;
- R(y) - единый фонд, включающий резервный фонд, фонд потребления и фонд накопления.
Понятно, что перечисленные показатели не являются независимыми.
Себестоимость продукции представляет собой сумму материальных затрат, амортизационных отчислений, коммерческих расходов, расходов на оплату труда и отчислений по заработной плате, то есть: S(y) = С0 + C0(y) + Sy) + Р2 Sy).
Валовая прибыль V(y) является разностью между доходом и себестоимостью: V(y) = W(y) - S(y).
Чистая прибыль P(y) определяется по валовой прибыли после уплаты соответствующих налогов: P(y) = (1 - рі) V(y).
Чистая прибыль может распределяться на фонды потребления, накопления и резервный фонд, то есть: (1 - pi) V(y) = R(y).
Собирая воедино четыре уравнения, приведенных выше, получаем следующее балансовое условие:
(1) R(y) = (1 - pi) [W(y) - Со - cc(y) - (1 + pi) o(y)\.
Введем следующее предположение: целью центра является максимизация единого фонда R(y), включающего резервный фонд, фонд потребления и фонд накопления. Другими словами, предположим, что целевая функция центра определяется величиной единого фонда, то есть F(y) = R(y).
Вспомним теперь, что в теоретико-игровой модели стимулирования центр стремится максимизировать разность между своим доходом и затратами на стимулирование J(y, o), то есть: F(o, y) = H(y) - J (y, o). Сравнивая это выражение с (1)1, замечаем, что в качестве функции дохода центра может рассматриваться следующая величина:
(2) H(y) = (1 - pi, [W(y) - Со - co(y)],
то есть разность между доходом организации и ее собственными затратами (т.е. всеми затратами за исключением затрат на стимулирование), а в качестве затрат на стимулирование:
Jy, o) = (1 - p1) (1 + pi) o(y).
Таким образом, в терминах основных показателей финансовохозяйственной деятельности организации теоретико-игровую задачу стимулирования можно сформулировать как задачу максимизации следующего критерия:
(3) (1 - pi [W(y) - Со - co0(y)\ - J(y, o) ® max,
o eM
при условии, что агент выбирает действие, доставляющее максимум его целевой функции при заданной системе стимулирования, то есть:
(4) у е Arg max [o(z) - c(z)}.
z^A
Итак, помимо функции затрат агента, в приведенной постановке задачи стимулирования фигурируют такие доступные из финансовой отчетности показатели (вопрос о достоверности значений этих показателей в настоящей работе не рассматривается) как: доход организации, ее постоянные и переменные издержки и ставки налогов.
Задача (3)-(4) является частным случаем задачи стимулирования, рассмотренной в первой части настоящей работы (в ней целевая функция центра имеет конкретный вид), следовательно для нее применимы детально проработанные в теории управления методы решения [14, 71-73].
Рассмотрим два примера, иллюстрирующих использование предложенного подхода к определению функции дохода центра.
Пример 4. В качестве первого примера возьмем механизм стимулирования работников предприятия (рабочих), перерабатывающего исходную продукцию, закупаемую на рынке, в конечную продукцию, продаваемую на рынке.
Представим производственное предприятие в виде двухуровневой организационной системы, на вернем уровне иерархии которой находится управляющий орган - центр, а на нижнем уровне -рабочие - агенты.
Для простоты рассмотрим случай одноэлементной системы с одним видом выпускаемой продукции. Предположим, что действием агента является выбор неотрицательного числа у 0, содержательно интерпретируемого как объем производства.
Пусть емкость рынка (спрос на продукцию данного предприятия) не ограничена. Обозначим: Pi - фиксированную цену продажи единицы конечной продукции. Тогда выручка предприятия от реализации равна: W(y) = Pi у.
Имеет место следующее балансовое условие (см. выражение
(1)):
(5) R(y) = {Pi у - со - co(y) - s(y) (i + Р2)} (i - pi).
Предположим, что цель центра (предприятия в целом) заключается в максимизации величины R(y). Управляющим воздействием центра является система стимулирования (зависимость вознаграждения агента от его действия), на которую наложим требование монотонности.
Обозначим целевую функцию центра Ф(у , о). Если при заданной системе стимулирования агент выбирает действие, которое максимизирует разность f(y, о) = о(у) - c(y) между стимулированием о(у) и его затратами c(y) по выбору этого действия, то задачу стимулирования можно записать в следующем виде (см. (3)-(4)):
(6) Ф(у*, о) = (1 - Pi) [Pi y* - Со - cdy*) - о(у*) (1 + Р2)} ® max,
о (- )
(7) y* е Arg max f(y, о).
y0
Для решения задачи (6)-(7) необходимо ввести определенные предположения относительно переменных издержек центра и функции затрат агента:
А.6. c0(y) - линейная функция: c0(y) = ay.
А.7. c(y) - монотонно возрастающая выпуклая гладкая функция, c(0) = cmin 0.
Содержательно, предположение А.6 означает, что функция переменных издержек центра обладает следующими свойствами. При нулевом объеме переменные затраты равны нулю.
С увеличением объема продаж возрастают, причем производство каждой единицы продукции требует одинаковых затрат. Содержательно, линейные переменные издержки могут соответствовать фиксированной цене a ?Pj единицы используемого сырья при пропорциональной технологии производства (см. свойства функции издержек в [43, 88])
Условие А.7 интерпретировалось выше (см. первую часть настоящей работы).
Предположим, что центру известна достоверно функция затрат c(y) агента.
В рамках введенных предположений оптимальной является, в частности, система стимулирования К-типа (см. первую часть
настоящей работы), которая в точности равна затратам агента: SK(y) = c(y). Поэтому задача (6)-(7) сводится к задаче оптимального согласованного планирования, то есть к задаче поиска действия агента у 0, реализация которого наиболее выгодна для центра:
(5) у* е Arg max {(Pi - a) x - со - (1 + p2) c(x)}.
x0
Рассмотрим условия индивидуальной рациональности:
(9)f(y*, s) 0, Ф(у*, s) 0,
которые требуют, чтобы значения целевых функций участников были неотрицательны .
В рамках введенных предположений целевая функция центра {(Pi - a) x - со - (1 + р2) c(x)} вогнутая, поэтому, если производство выгодно, то существует отрезок [у1; у2], на котором эта целевая функция положительна. Тогда центру выгодно побуждать агента выбрать одно из действий у из отрезка [у1; у2].
Поэтому рассмотрим следующую (компенсаторно-аккордную) систему стимулирования s, график которой приведен на рисунке 36. При действии агента, меньшем у е [у1; у2], положим S (у) = cmin, то есть агент получает минимальное вознаграждение cmin (увеличение вознаграждения по сравнению с этой величиной не имеет смысла); при у у S (у) = с(у*), то есть выбор больших действий не поощряется, но условие монотонности выполнено.
Легко видеть, что при использовании центром системы стимулирования s агент выберет объем производства у , за который центр его еще поощряет.
Содержательно, агенту гарантируется минимальное вознаграждение cmin, независимо от его действий (см. рисунок 36). Если объем производства превышает величину у*, то агент получает за это премию (c(y ) - cmin), компенсирующую его затраты. При дальнейшем росте объема производства вознаграждение остается постоянным, а так как затраты агента при этом возрастают, то выбор действий, превышающих у , для него невыгоден. -
Пример 5. В качестве второго (более сложного) примера возьмем механизм стимулирования, побуждающий работников торговых компаний (менеджеров по продажам) увеличивать объем продаж в интересах компании в целом [29].
Представим торговую компанию в виде двухуровневой организационной системы, на вернем уровне иерархии которой находится управляющий орган - центр, а на нижнем уровне - менеджеры по продажам - агенты.
Рассмотрим случай одноэлементной системы с одним видом товара. Предположим, что действием агента является выбор неотрицательного числа у 0, содержательно интерпретируемого как объем продаж.
Пусть емкость конкурентного рынка не ограничена. Обозначим: Р0 - фиксированную цену закупки, Pj - фиксированную цену продажи. Тогда доход компании равен: W(y) = Pj у, а валовая прибыль: V(y) = (Pj - Ро) у.
Для простоты предположим, что налоги отсутствуют, тогда, если о(у) - величина вознаграждения агента, а R(y) - величина единого фонда, то имеет место следующее балансовое условие (см. выражение (1)):
(10) R(y) = {(Pj - Ро) у - со - Со(у) - о(у)}.
В данном случае функцией дохода центра является следующее выражение: H(y) = (Pj - P0) у - с0 - c0(y).
Как и ранее, предположим, что цель центра (компании в целом) заключается в максимизации величины R(y). Управляющим воздействием центра является система стимулирования (зависимости вознаграждения агента от его действия), на которую наложим требование монотонности. Задачу стимулирования можно записать в следующем виде (см. (3)-(4)):
(11) F(y*, s) = {(P! - Po) y - со - co(y*) - s(y*)} max,
s (- )
(12) y* e Arg max f(y, s).
y0
Введем следующее предположение относительно переменных издержек центра (будем считать, что функция затрат агента удовлетворяет предположению А.2''):
А.8. c0(y) - монотонно возрастающая гладкая функция, такая, что c0(0) = 0, $ y’ 0: c0(y) - вогнутая функция при y ?y’ и выпуклая при y y’.
Содержательно, предположение А.1а означает, что функция переменных издержек центра обладает следующими свойствами. При нулевом объеме продаж переменные затраты равны нулю.
С увеличением объема продаж затраты возрастают, причем при объемах продаж, меньших величины y’ 0, каждое последующее увеличение объема продаж требует меньших затрат, чем предыдущее (предельные затраты убывают), а при объемах продаж, больших величины y’ 0, каждое последующее увеличение объема продаж требует больших затрат, чем предыдущее (предельные затраты возрастают). График функции c0(y), удовлетворяющей предположению А.8, приведен на рисунке 37.
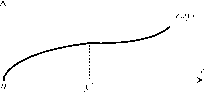
Рис. 37. Функция переменных издержек центра
Предположим, что центру неизвестна достоверно функция затрат агента, но ему известен диапазон возможных значений функции затрат, то есть он знает, что у е A c_(y) ? c(y) ? c+(y), где функции c-(y) и c+(y), определяющие границы диапазона возможных значений затрат агента, удовлетворяют предположению А.2' (см. рисунок 38).
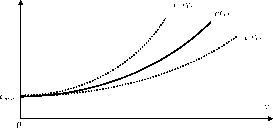
Рис. 38. Диапазон возможных значений функции затрат агента
В рамках введенных предположений оптимальной является система стимулирования К-типа, которая в точности равна затратам агента: sK(y) = c(y). Поэтому задача (11)-(12) сводится к задаче оптимального согласованного планирования, то есть к задаче поиска действия агента у 0, реализация которого наиболее выгодна для центра:
(13) у* е Arg max {(Pi - Po) x - со - co(x) - c(x)}.
x0
Обозначим характерные точки функции H(y) дохода центра следующим образом:
уі = min {у 0 | H(y) = 0}, у2 = arg max H(y),
у0
У3 = max {у 0 | H(y) = 0}.
Очевидно, что в рамках введенных предположений выполнено:
У1 ? У2 ? У3, У’ ? У2.
Содержательно, если функция переменных издержек центра имеет вид, приведенный на рисунке 37, то при малых объемах продаж величина дохода отрицательна и убывает с ростом объема продаж. Достигнув минимума, она начинает возрастать, становится в точке у1 положительной, достигает максимума в точке у2, а затем убывает и становится отрицательной после точки у3 (см. рисунок 39).
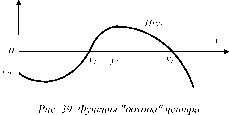
Запишем условие индивидуальной рациональности (9) в следующем виде: fy , s) 0, Ф(у , S) 0.
Центру выгодно побуждать агента выбрать одно из действий у из отрезка \уу у2] при условии, что Ф(у) c(y). Обозначим характерные точки целевой функции центра:
у- = arg max Ф(у, с_(у)),
{у 0| H (у) с - (у)}
у+ = arg max Ф(у, с+(у)).
{у 0| H (у) с + (у)}
В рамках введенных предположений выполнено:
(14) уі ? у + ? у- ?у2 ?у3.
Таким образом, центру заведомо невыгоден выбор агентом
* *
действий, не принадлежащих отрезку \ у+ ; у- ]. Поэтому рассмотрим следующую систему стимулирования s, график которой
*
приведен на рисунке 40. При действии агента, меньшем у+, положим s (у) = cmin, то есть агент получает минимальное вознаграждение cmin (увеличение вознаграждения по сравнению с этой величи**
ной не имеет смысла); при у е \ у+; у- ] агенту гарантированно
компенсируются затраты, то есть s (y) = c+(y); а при y у_
s (y) =c+( у_), то есть выбор больших действий не поощряется, но условие монотонности выполнено. Легко видеть, что, если затраты агента строго меньше максимально возможных (c(y) c+(y)), то он
выберет максимальный объем продаж y = y_, за который центр его еще поощряет, то есть данная система мотивации стимулирует рост объемов продаж.
Содержательно, агенту гарантируется минимальное вознаграждение cmin, независимо от его действий (см. рисунок 40). Если
объем продаж превышает величину y+, то агент получает за это *
премию (c+( y+) - cmin). При дальнейшем росте объема продаж вознаграждение возрастает, причем не медленнее, чем растут затраты (побуждение к увеличению объема продаж).
При превышении объемом продаж величины y_ вознаграждение остается постоянным (так как затраты агента при этом возрастают, то выбор действий, превышающих y_, для него невыгоден).
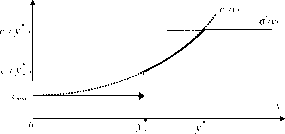
Рис. 40. Система стимулирования s*
Предложенная система стимулирования s (несмотря на то, что ее оптимальность для общего случая не доказана) обладает следующими положительными свойствами. Во-первых, она учитывает специфику торговой компании (см. выражения (10)-(11) и предпо-98
ложение А.8), во-вторых, она является минимальной (с точки зрения затрат центра на стимулирование) системой стимулирования, которая одновременно гарантированно (в рамках существующей информированности центра) реализует выгодные для центра действия и (если реальная функция затрат агента оказывается меньше максимальной) побуждает агента выбирать максимальные действия, то есть делает выгодным увеличение объема продаж. -
ЗАКЛЮЧЕНИЕ
Таким образом, в настоящей работе предложены и изучены базовые системы стимулирования в организационных системах.
Отличительной чертой базовых систем стимулирования является, во-первых, то, что они являются простейшими (то есть легко поддающиеся анализу, в том числе - теоретико-игровому) элементами конструктора, из которых могут быть собраны любые (по крайней мере - все встречающиеся на сегодняшний день на практике) системы индивидуальной оплаты труда.