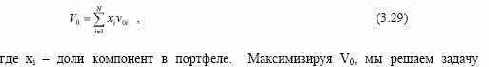инвестора, направленная на снижение системных инвестиционных рисков и
использующая производные ценные бумаги. Базовым средством хеджирования
реальных активов (акции, облигации), именуемых в теории хеджирования
подлежащими активами, является покупка опционов put на эти активы. Целью
такой покупки является лимитирование, отсечение убытков, связанных с резким
падением цены активов на рынке.
Хеджирование . крайняя мера, вызванная недостатком информации о
тенденциях поведения подлежащего опциону актива в будущем (в противном
случае потенциально падающий актив мог быть вовремя продан, а затем куплен
обратно, но по более низкой цене). Инвестор, идя на выплату опционной премии,
заведомо снижает ожидаемую доходность своих вложений. В то же время он
снижает и риск вложений, лимитируя убытки заранее известной величиной. Таким
образом, снижается волатильность вложений.
Косвенным эффектом хеджирования является повышение ликвидности
активов инвестора. Получая опционную выплату в случае паденияцены актива,
инвестор получает поток денежных средств, которые могут быть направлены на
инвестиции.
Надо обязательно добавить, что опционы и фьючерсы в странах с
недоразвитой экономикой . это вовсе не панацея от финансовых крахов. У многих
на памяти истории августа 1998 года, когда люди, захеджировавшие свои рублевые
позиции, понесли колоссальные убытки из-за отказа проигрывающих сторон в
полном объеме исполнять свои обязательства по долларовым фьючерсам, что
вызвало принудительное закрытие позиций. Полностью эти позиции не могли быть
закрыты уже потому, что вариационная маржа в большом процентном отношении
была обеспечена государственными краткосрочными облигациями, по которым как
раз был объявлен дефолт. Таким образом, убытки хеджеров оказались
двусторонними: от вложений в ГКО по факту дефолта и от вложений во фьючерсы
по факту недовыплаченной вариационной маржи.
Тем не менее, в спокойные времена деривативы являются естественным средством управления фондовыми рисками, и именно в этом надежном качестве мы их здесь и рассматриваем. Когда хеджируется не отдельный актив, а совокупность активов, портфель реальных бумаг (в частном случае это пай взаимного фонда), тогда хеджирование идет на индексной основе. Проводится стилевой анализ совокупности активов, по результатам которого устанавливается модельный портфель, наполненный модельными активами в той пропорции, чтобы построенный модельный портфель наилучшим образом отвечал портфелю реальному. Каждому модельному активу соответствует фондовый индекс, и, чтобы осуществить хеджирование модельного актива, необходимо приобрести соответствующее количество индексных опционов.
Например, по состоянию на 11 декабря 2001 года, американский инвестор имеет 1 миллион 26 тыс. долларов, вложенных в высококапитализированные акции американских компаний. Будем для простоты считать, что стилевой анализ показывает 100%-ое соответствие вложений индексу S&P500. Инвестор принимает решение хеджировать портфель индексными опционамисо страйком, ближайшим к котировке индекса на текущую дату (S0 = 1142). При этом он хеджируется из расчета на Т = 1 месяц = 1/12 года существования портфеля. Результатом хеджирования является приобретение индексных опционов с тикером SPT MH-E, страйк dP = 1140, дата погашения . 18 января 2002 года.
Общее их количество определяется из того расчета, что один базисный пункт индексного опциона покрывает 100 долларов подлежащего ему актива. Чтобы захеджировать 1 млн. долларов опционами данного тикера, необходимо приобрести 1026000 : 1140 : 100 = 9 стандартных опционных контрактов.
В данном случае v = 34.5% годовых, без учета реинвестирования. Наоборот, если индекс упадет, например, до SТ = 1072, то есть на 6 процентов вниз, тогда put-опцион оказывается в деньгах, и доходность вложений, согласно (3.24), становится равной v = - 33.1% годовых. Если бы опцион не приобретался, то простейшие вычисления дают доходность подлежащего актива 72% годовых при первом сценарии развития событий и (-72%) годовых . при втором сценарии. Видим, что волатильность вложений, измеренная как разбег доходности применительно к двум сценариям развития событий, вполовину меньше для хеджированного актива.
граничный нижний уровень доходности сборки «put + актив», который известен заранее при ее покупке,


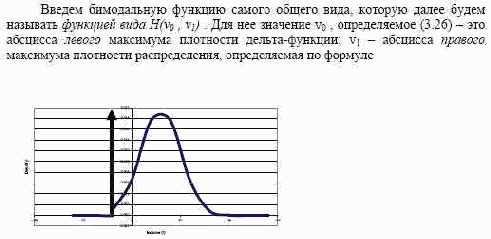
Что касается вида , то удобно искать эту функцию в виде плотности гауссовского распределения с нечеткими параметрами среднего и среднеквадратического отклонения, как это обосновывается в [53]. Тогда (5.24) имеет вид усеченной слева плотности нормального распределения с нечеткими параметрами, с дельта-функцией на левом конце распределения, бимодальной формы (рис. 3.5).
Рис. 3.5. Плотность распределения доходности сборки Вводя этот обобщенный вид бимодальной функции, мы сознательно не настаиваем на том, что непрерывная ее часть будет иметь нормальный вид.



Можем ли мы, зная распределения доходности отдельных хеджированных активов, получить распределение доходности модельного портфеля на их основе аналитическим путем? К величайшему сожалению, нет. Математическая теория композиции вероятностных распределений свидетельствует о том, что сумма двух стохастически зависимых случайных величин с усеченно-нормальным распределением есть случайная величина, не обладающая усеченно-нормальным распределением. В результирующем вероятностном распределении такой величины плотность является мультимодальной функцией. Все это говорит о том, что точному аналитическому решению задача оптимизации модельного портфеля с хеджированными активами не поддается.
В качестве альтернативы можно предолжить для оптимизации хеджированного модельный портфеля схему минимизации уровня предельных потерь. Действительно, по каждому хеджированному активу известна минимальная доходность v0i. Соответственно, минимальная доходность по портфелю составляет нелинейной оптимизции относительно не только оптимального распределения долей активов, но и глубины их хеджирования, а также соотношения страйков по put-опционам и размеров опционных премий.
Оптимизация функционала (3.29) не является оптимизацией модельного портфеля в постановке Марковица уже потому, что в качестве ограничения в задаче оптимизации здесь не выступает риск портфеля. Чтобы учесть параметры риска в оптимизации, можно перед решением задачи (3.29) решить классическую задачу Марковица, а в задаче (3.29) оптимизировать уже только параметры хеджирования, зафиксировав веса компонент. Такой компромисс позволяет избежать применения статистического моделирования портфеля в духе Монте- Карло, которое я лично считаю недопустимой методикой для оптимизации фондового портфеля.