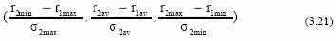предложенный Гарри Марковицем в [134]. Суть его в следующем.
Пусть портфель содержит N типов ценных бумаг (ЦБ), каждая из которых
характеризуется пятью параметрами:
- начальной ценой Wi0 одной бумаги перед помещением ее в портфель;
- числом бумаг ni в портфеле;
- начальными инвестициями Si0 в данный портфельный сегмент, причем
Сам портфель характеризуется:
- суммарным объемом портфельных инвестиций S;
- долевым ценовым распределением бумаг в портфеле {xi}, причем для
исходного портфеля выполняется
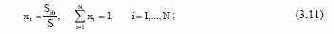Замечание. В подходе Марковица к портфельному выбору под риском
понимается не риск неэффективности инвестиций, а степень колеблемости
ожидаемого дохода по портфелю, причем как в меньшую, так и в большую
сторону. Можно без труда перейти от задачи вида (3.14) к задаче, где в качестве ограничения вместо фиксированного стандартного отклонения выступает вероятность того, что портфельная доходность окажется ниже заранее обусловленного уровня. Выражение (3.15), именуемое эффективной границей портфельного множества, в координатах «риск-доходность» является кусочно-параболической вогнутой функцией без разрывов. Правой точкой границы является точка, соответствующая тому случаю, когда в портфеле оказывается одна бумага с максимальной среднеожидаемой доходностью.
Подход Марковица, получивший широчайшее распространение в практике управления портфелями, тем не менее имеет ряд модельных допущений, плохо согласованных с реальностью описываемого объекта - фондового рынка. Прежде всего это отсутствие стационарности ценовых процессов, что не позволяет описывать доходность бумаги случайной величиной с известными параметрами. То же относится и корелляции.
Если же мы рассматриваем портфель из модельных классов, а ценовую предысторию индексов модельных классов - как квазистатистику, то нам следует моделировать эту квазистатистику многомерным нечетко-вероятностным распределением с параметрами в форме нечетких чисел. Тогда условия (3.12) . (3.13) запиываются в нечетко-множественной форме, и задача квадратичной оптимизации также решается в этой форме. Решением задачи является эффективная граница в виде нечеткой функции полосового вида. Каждому отрезку на эффективной границе, отвечающей абсциссе портфельного риска, соответствует нечеткий вектор оптимальных портфельных долей.
И, наконец, если нам заданы контрольные нормативы по доходности и риску (бенчмарк модельногопортфеля), которые нам следует соблюсти в нашем портфеле, увеличивая доходность и одновременно снижая риск. Если бенчмарк попадает в полосу эффективной границы, то возникает дабл-риск (по факторам доходности и волатильности), что модельный портфель «не переиграет» бенчмарк. Этот риск можно оценить по методу из [53, 56, 59].
Итак, изложение модифицированного подхода Марковица завершено. Далее по тексту статьи мы считаем, что имеем дело с квазистатистикой модельных индексов в портфеле, которая моделируется нами посредством N-мерного нечетко- вероятностного распределения. Оценив параметры этого распределения как нечеткие числа, мы решаем задачу квадратичной оптимизации в нечеткой постановке, получая эффективную границу в форме криволинейной полосы. Рассмотрим простейший пример американского модельного портфеля из двух модельных классов: правительственных долгосрочных облигаций (Класс 1, характеризующийся индексом LB Govt Bond) и высококапитализированных акций (Класс 2, характеризующийся индексом S&P500). Сводные данные по обоим индексам приведены в таблице 3.4.
Таблица 3.4. Исходные данные по модельным классам Нам следовало бы еще оценить корреляцию двух индексов. Но, как я покажу далее, в нашем случае этого не потребуется. Пока же для общности обозначим коэффициент корреляции .
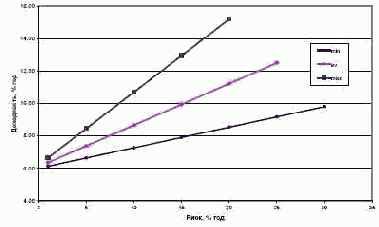
Надо сразу оговориться, что случай портфеля из двух компонент является вырожденным с точки зрения оптимизации. Здесь полное множество портфельных решений представляет собой участок в общем случае кривой линии на плоскости, и он же является эффективной границей. Так что в настоящем примере мы не сколько решаем оптимизационную задачу, сколько ищем аналитический вид эффективной границы в координатах «риск-доходность». Запишем (3.12) . (3.13) в частном виде уравнение эффективной границы в виде полосы с прямолинейными границами (см. рис. 3.4).
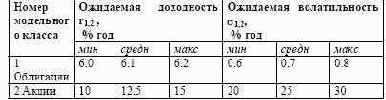
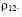
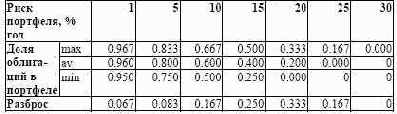
Рис. 3.4. Эффективная граница в виде полосы с линейными границами Коэффициент пропорциональности в (3.20) есть не что иное, как хорошо известный в портфельном менеджменте показатель Шарпа [146] . отношение доходности индекса (за вычетом безрисковой составляющей доходности) к волатильности индекса. Только в нашем случае он имеет нечеткий вид, сводимый к треугольному по правилу: В таблицу 3.5 сведены границы для модельного класса облигаций в структуре модельного портфеля для различных уровней риска. Таблица 3.5. Оптимальная доля облигаций в портфеле По краям полосы разброс портфельных границ ниже, чем в середине. Это объясняется тем, что на краях полосы эффективной границы портфель обладает вполне определенным стилем: большей доходности отвечает модельный класс акций, а меньшему риску . модельный класс облигаций.
