20.3.3 Бинарные переменные
Здесь, как правило, речь идёт о переменных, которые указывают на факт осуществления некоторого события или выполнения определённого критерия. В файле данных это обстоятельство должно быть закодировано при помощи двух численных значений, причём в соответствии с установками по умолчанию, SPSS для кодировки осуществления события ожидает цифру 1.
Если сопоставить друг с другом две переменные, то все возможные сочетания наблюдений дают четыре различные частоты, которые называются а, Ь, с, d и имеют следующий смысл:
| Переменная 2 | |||
| сбылось | не сбылось | ||
|
Переменная 1 |
Сбылось |
а |
b |
| Не сбылось | с | d | |
На основании этих частот, можно рассчитать множество различных дистанционных мер, 27 из которых применяются в SPSS. Двадцать разновидностей мер, называемых мерами подобия, рассмотрены в разделе 15.4. Остальные приводятся ниже.
Квадрат евклидовою расстояния
Бинарное евклидово расстояние, возведенное в квадрат, представляет собой количество наблюдений, для которых, по крайней мере, один из критериев присутствует и один отсутствует. Эта мера является установкой по умолчанию.
dist= b + с
Евклидово расстояние
Бинарное евклидово расстояние представляет собой корень из числа наблюдений, для которых, по крайней мере, один из критериев присутствует и один отсутствует.
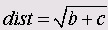
Разность длин
Эта мера имеет минимальное значение равное 0 и не имеет верхнего придела.
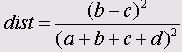
Образцовая разность
Образцовая разность может принимать значения от 0 до 1.
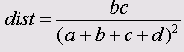
Дисперсия
Дисперсия имеет минимальное значение равное 0 и не имеет верхнего придела.
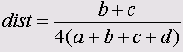
Форма
У этой дистанционной меры нет ни нижнего ни верхнего предела
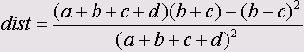
Мера Ланса и Уильямса (Lance and Williams)
Эта мера может принимать значения от 0 до 1.
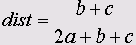
Приведенные меры отличаются друг от друга присутствием в соответствующей формуле различных наборов из четырёх частот: а, b, с и d
Так, для евклидовой меры в расчёт включают только те наблюдения, для которых имеется один признак и отсутствует другой, а в других дистанционных формулах учитываются все частоты. Исключением является дистанционная мера по Лансу и Уильямсу, в которой в расчет не берутся те наблюдения, для которых отсутствуют оба признака.
На какой мере Вы остановите свой выбор, зависит от того, какую роль вы отводите частотам а, b, с и d.
