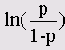16.7 Пробит-анализ
Этот метод известен также под именем "Дозаторный анализ кривых воздействия" и находит применение преимущественно в области токсикологии. В большинстве случаев речь идёт о том, как на заданное количество индивидуумов воздействуют различные дозировки некоторого вещества (к примеру, некоторого токсичного вещества).
Классический пример, который вошёл и в справочник по SPSS, исследует действие средства, предназначенного для уничтожения насекомых. При этом производится подсчёт, сколько насекомых из заранее известного количества погибли при воздействии определённых доз вещества. Особенный интерес в данном случае представляет дозировка, при которой уничтожается половина имеющихся насекомых.
Оставим животных в покое и обратимся, в виде исключения, к одному специально придуманному примеру. Шеф секретной службы некоторой вымышленной страны пожелал узнать, сколько денег он должен предложить гражданам соседнего государства, чтобы они доставляли ему некоторую тайную информацию. Для этой цели через своего посредника он предлагает первой группе 1000 долларов и отмечает, сколько человек соглашаются на его предложение вести шпионскую деятельность. Второй группе он предлагает 2000 долларов и вновь отмечает себе количество попаданий в цель. Он продолжает предлагать деньги и дальше, действуя таким пошаговым образом и доходит до суммы 10000 долларов. При этом исследованиям подвергаются две различные категории людей. К первой категории относятся люди, которые недовольны своим материальным положением, ко второй — люди, удовлетворенные своим материальным положением.
Для обеих категорий шеф секретной службы желает выяснить, сколько он должен предложить денег, чтобы достичь желаемой доли положительных ответов. К примеру, его интересует сумма, которую он должен заплатить, чтобы на его предложение согласилась половина опрашиваемой группы.
Для обеих категорий удовлетворенности материальным положением (доволен — недоволен) в нижеследующей таблице представлены долларовые суммы в порядке возрастания, количество вовлечённых в эксперимент людей (nges) и количество фактически завербованных шпионов (п).
|
группа |
доллар |
количество вовлечённых в эксперимент людей |
количество фактически завербованных шпионов |
|
недоволен |
1000 |
59 |
8 |
|
недоволен |
2000 |
56 |
22 |
|
недоволен |
3000 |
53 |
28 |
|
недоволен |
4000 |
49 |
30 |
|
недоволен |
5000 |
51 |
35 |
|
недоволен |
6000 |
43 |
34 |
|
недоволен |
7000 |
40 |
36 |
|
недоволен |
8000 |
45 |
41 |
|
недоволен |
9000 |
40 |
38 |
|
недоволен |
10000 |
35 |
34 |
|
доволен |
1000 |
61 |
1 |
|
доволен |
2000 |
45 |
13 |
|
доволен |
3000 |
52 |
21 |
|
доволен |
4000 |
45 |
22 |
|
доволен |
5000 |
46 |
26 |
|
доволен |
6000 |
38 |
27 |
|
доволен |
7000 |
45 |
35 |
|
доволен |
8000 |
42 |
33 |
|
доволен |
9000 |
37 |
32 |
|
доволен |
10000 |
36 |
33 |
Эта информация построчно хранится в файле dollar.sav (переменные: gruppe, dollar, nges, n).
-
Откройте файл dollar.sav.
-
Выберите в меню Analyze (Анализ) Regression (Регрессия) Pmbit... (Пробит)
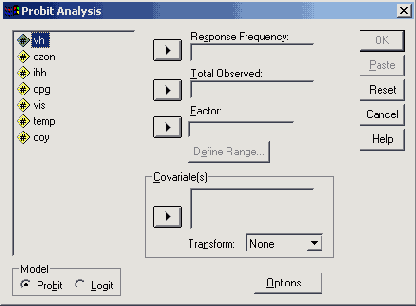
Откроется диалоговое окно Probit Analysis (Пробит-анализ).
Рис. 16.22: Диалоговое окно Probit Analysis (Пробит-анализ)
-
Поочерёдно перенесите переменные п в поле частоты отклика, переменную nges в поле наблюдаемого общего количества, переменную gruppe в поле факторов и переменную dollar в поле ковариат.
-
При помощи соответствующей кнопки для факторной переменной необходимо определить область принадлежности; для нашего примера она равна целым числам: 1 и 2.
-
Стандартным подходом при проведении пробит-анализа стало логарифмическое преобразование значений ковариат (при помощи десятичного логарифма); задайте и Вы это преобразование.
-
Оставьте установку обычной пробит-модели и щёлкните на кнопке опций. Дополнительно к установленным статистикам активируйте тест параллельности, который является уместным при анализе разнообразных групп.
-
Начните расчёт нажатием ОК.
Результирующие данные выводятся в старой табличной форме и являются довольно обширными. На одном из первых шагов определяются так называемые "пробиты". Они представляют собой стандартные значения, которые отвечают площади под частью кривой стандартной нормального распределения, соответствующей отношению частоты положительных ответов к общей частоте. Так, в первой группе, которой предлагалось по 1000 долларов, это предложение приняли 8 человек из 59, что соответствует относительной доле, равной
р=8/59= 0,1356
Это значение интерпретируется как часть площади под кривой стандартного нормального распределения (которая, как известно, суммарно нормирована к 1). По соответствующей статистической таблице можно установить, что стандартное значение равно -1,10. Это значение является пробитом к дозировке 1000 долларов.
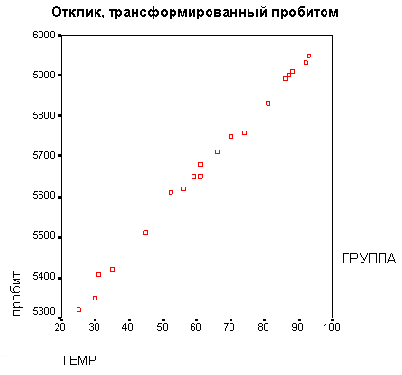
Упомянутые пробиты для обеих групп в зависимости от логарифма дозировки представлены на одной диаграмме, которую вы можете увидеть в окне просмотра:
Для обеих групп график является практически линейным, что является предпосылкой для дальнейших рассуждений. В противном случае дополнительно следовало было бы рассматривать ход процесса воздействия на основе исходных значений (то есть без логарифмического преобразования).
Рис. 16.23: Отклики, трансформированные пробитом
Для обеих кривых определяется уравнение регрессионных прямых, причём для обеих прямых вычисляется общий угол наклона:
|
Regression Coeff. |
Standard Error |
Coeff./S.E. | ||||
|
DOLLAR |
2,78749 |
,17640 |
15,80205 | |||
|
Intercept |
Standard Error |
Intercept/S.E. |
GRUPPE | |||
| -9 ,59552 | ,63415 | -15, 13130 | 1 | |||
| 2 | ||||||
| -9 ,99490 | ,64731 | -15,44060 | ||||
| Pearson Goodness -of -Fit Chi Square=10,043 DF = 17 P = ,902 | ||||||
|
Parallelism Test Chi Square = ,164 DF = 1 P = ,686 | ||||||
При тесте на качество согласия большое значение р (как в рассматриваемом примере) указывает на лучшее приближение. Второй тест по критерию хи-квадрат проясняет вопрос, действительно ли обе прямые могут рассматриваться как параллельные. Параллельности прямых соответствует незначимый результат теста (как в рассматриваемом случае).
Если мы рассмотрим уравнение регрессии для первой группы, то получим следующее уравнение, прогнозирующее значение пробита:
Probit= 2,78749xlog(Dollar)- 9,59552
Для значения 1000 долларов получим
Probit= 2,78749x3- 9,59552= - 1,2331
Если мы вновь обратимся к статистической таблице, содержащей значения стандартной кривой нормального распределения, то полученному стандартизированному значению в данном случае соответствует площадь 0,10878. Это значение используется для того, чтобы определить ожидаемую частоту отклика:
59x0,10878= 6,418
Полученные результаты сведены в следующую таблицу:
|
Number of Observed Expected | |||||||||||
|
GRUPPE |
DOLLAR |
Subjects Responses Responses Residual |
Prob | ||||||||
|
1 |
3 |
, 00 |
59 |
,0 |
8 |
,0 |
|
6,418 |
1 |
,582 |
,10878 |
|
1 |
3 |
,30 |
56 |
,0 |
22, |
0 |
19 |
,422 |
2 |
,578 |
,34681 |
|
1 |
3 |
,48 |
53 |
,0 |
28, |
0 |
28 |
,546 |
- |
,546 |
,53860 |
|
1 |
3 |
, 60 |
49 |
,0 |
30, |
0 |
32 |
, 923 |
- |
2, 923 |
, 67191 |
|
1 |
3 |
,70 |
51 |
,0 |
35, |
0 |
38 |
, 902 |
- |
3, 902 |
,76279 |
|
1 |
3 |
,78 |
43 |
,0 |
34, |
0 |
35 |
,491 |
- |
1,491 |
,82537 |
|
1 |
3 |
, 85 |
40 |
,0 |
36, |
0 |
34 |
,768 |
1 |
,232 |
,86921 |
|
1 |
3 |
, 90 |
45 |
,0 |
41, |
0 |
40 |
,522 |
, |
478 |
, 90048 |
|
1 |
3 |
, 95 |
40 |
,0 |
38, |
0 |
36 |
,928 |
1 |
,072 |
, 92319 |
|
1 |
4 |
,00 |
35 |
,0 |
34, |
0 |
32 |
,899 |
1 |
,101 |
, 93996 |
|
2 |
3 |
,00 |
61 |
,0 |
1, |
0 |
3, |
129 |
- |
2,129 |
,05129 |
|
2 |
3 |
,30 |
45 |
,0 |
13, |
0 |
9, |
621 |
3 |
,379 |
,21380 |
|
2 |
3 |
,48 |
52 |
,0 |
21, |
0 |
19 |
,820 |
1 |
,180 |
,38115 |
|
2 |
3 |
,60 |
45 |
,0 |
22, |
0 |
23 |
,322 |
- |
1,322 |
,51826 |
|
2 |
3 |
,70 |
46 |
,0 |
26, |
0 |
28 |
,703 |
- |
2,703 |
,62397 |
|
2 |
3 |
,78 |
38 |
,0 |
27, |
0 |
26 |
,761 |
, |
239 |
,70425 |
|
2 |
3 |
,85 |
45 |
,0 |
35, |
0 |
34 |
,436 |
, |
564 |
,76524 |
|
2 |
3 |
,90 |
42 |
,0 |
33, |
0 |
34 |
,100 |
- |
1,100 |
,81190 |
|
2 |
3 |
,95 |
37 |
,0 |
32, |
0 |
31 |
,373 |
f |
627 |
,84791 |
|
2 |
4 |
,00 |
36 |
/o |
33, |
0 |
31 |
,535 |
1 |
,465 |
,87597 |
Сразу же после этой таблицы для заданных вероятностей ( вероятности здесь следует понимать, как отношение частоты желательного отклика к общему числу испытуемых) выводятся значения необходимых дозировок (в нашем случае: денежная сумма в долларах) и их 95%-ый доверительный интервал. Ниже приводится таблица значений для первой группы:
|
95% Confidence Limits | |||
|
Prob |
DOLLAR |
Lower |
Upper |
|
,01 |
405,30868 |
289,59056 |
529,15509 |
|
,02 |
507,66784 |
373,66257 |
647,93485 |
|
,03 |
585,63448 |
439,14578 |
736,94514 |
|
, 04 |
652,08194 |
495,79196 |
811,99633 |
|
,05 |
711,65439 |
547,15681 |
878,74346 |
|
,06 |
766,62851 |
594,99562 |
939,94335 |
|
, 07 |
818,31336 |
640,32303 |
997,17444 |
|
,08 |
867,54082 |
683,78664 |
1051,43643 |
|
,09 |
914,87813 |
725,82978 |
1103,40905 |
|
,10 |
960,73191 |
766,77131 |
1153,57841 |
|
, 15 |
1176,35221 |
961,74200 |
1387,62679 |
|
,20 |
1381,73708 |
1150,43739 |
1608,52696 |
|
,25 |
1586,29202 |
1340,43221 |
1827,40833 |
|
,30 |
1795,67203 |
1536,35222 |
2050,97344 |
|
,35 |
2014,28728 |
1741,83765 |
2284,49983 |
|
,40 |
2246,29254 |
1960,31730 |
2533,03836 |
|
,45 |
2496,16365 |
2195,45599 |
2802,13038 |
|
,50 |
2769,19498 |
2451,53866 |
3098,44683 |
|
,55 |
3072,09057 |
2733,92871 |
3430,56245 |
|
, 60 |
3413,82108 |
3049,73874 |
3810,08632 |
|
,65 |
3807,02441 |
3408,93562 |
4253,51516 |
|
, 70 |
4270,51303 |
3826,32195 |
4785,56534 |
|
,75 |
4834,19240 |
4325,40532 |
5445,75782 |
|
,80 |
5549,85527 |
4946,81830 |
6303,01441 |
|
,85 |
6518,83063 |
5769, 66817 |
7493,47901 |
|
, 90 |
7981,87380 |
6980,17468 |
9345,15098 |
|
, 91 |
8381,92608 |
7305,70121 |
9861,25890 |
|
,92 |
8839,28528 |
7675,37386 |
10455, 92397 |
|
, 93 |
9371,03216 |
8102,08907 |
11153,16983 |
|
,94 |
10002,81198 |
8605,11895 |
11989,28434 |
|
,95 |
10775,51263 |
9215,02568 |
13022,52271 |
|
, 96 |
11759, 93430 |
9984,40147 |
14354,56418 |
|
, 97 |
13094,24400 |
11015,11467 |
16185,74513 |
|
,98 |
15105,23259 |
12545,80989 |
18995,72850 |
|
, 99 |
18920,00171 |
15388,14261 |
24468,76250 |
Для того, чтобы переманить на свою сторону половину группы граждан чужой страны, недовольных своим финансовым положением (Prob = 0,5), начальник секретной службы должен предложить каждому по 2769 долларов, причём с 95%-ой вероятностью эта сумма колеблется от 2452 до 3098 долларов. Для группы довольных финансовым положением (для которой распечатка данных здесь не приведена) придётся заплатить больше: 3852 доллара, с 95%-ым доверительным интервалом эта сумма колеблется от 3437 до 4296 долларов.
Отношение этих двух значений медиан составит:
2769/3852= 0,719
Это соотношение отображается в небольшой статистической сводке:
|
Estimates of Relative Median Potency | |||
|
|
95% |
Confidence |
Limits |
|
GRUPPE 1 VS. 2 |
Estimate ,7190 |
Lower ,60280 |
Upper ,84419 |
Если Вы в диалоговом окне выберите не пробит, а логит-модель, то отношение частоты положительных откликов к общему количеству опрашиваемых р заменяется выражением