11.3.5 Другие меры связанности
SPSS позволяет вычислить другие специальные меры связанности, обзор которых приводится ниже.
Эта
Этот коэффициент применяется, если зависимая переменная принадлежит к интервальной шкале, а независимая — к порядковой или шкале наименований, эта2 представляет собой долю общей дисперсии, которую можно объяснить влиянием независимой переменной.
Коэффициент каппа (к)
Коэффициент каппа Козна (к) можно вычислить только для квадратных таблиц сопряженности, в которых применяются одинаковые числовые кодировки для переменных строк и столбцов. Типичный случай применения этого критерия — оценка людей или объектов двумя экспертами. В таком случае к указывает на степень согласия между экспертами.
Мера риска
С помощью этой опции в SPSS реализован расчет трех различных коэффициентов, которые могут быть определены для таблицы сопряженности, состоящей из 2 строк и 2 столбцов, созданной на основании строго определенных правил, которые будут сформулированы в конце данного параграфа. При расчете меры риска анализируется так называемая переменная риска, которая имеет две категории и указывает, произошло ли определенное событие или нет. Анализ переменной риска проводится в зависимости от причинной (независимой) переменной, которая должна также быть дихотомической.
Это положение можно пояснить на типичном примере. Исследование депрессии на базе 294 респондентов дало следующую частотную таблицу:
|
Депрессия |
Да |
Нет |
|
Женщины |
а = 40 |
Ь = 143 |
| Мужчины | с = 10 | d = 101 |
Обе переменные, входящие в таблицу, — являются дихотомическими. Депрессия, имеющая две категории (да-нет), является переменной риска, а пол с двумя категориями (женщины-мужчины) — независимой (причинной) переменной.
Исследование, проводимое в такой форме, называется групповым или когортным. При когортном исследовании определенная группа наблюдений, в которых анализируемое событие еще не произошло, изучается на протяжении известного промежутка времени. Определяется, в каких наблюдениях данное событие произошло, а в каких — нет, и различается ли риск наступления события между разными категориями независимой переменной. При групповых исследованиях группа наблюдений, в которых событие уже произошло, сравнивается с контрольной группой.
Два из трех коэффициентов риска, определяемых в SPSS, обычно относятся к когортным исследованиям, а третий — к групповым. При когортном исследовании для обеих категорий независимой переменной (в данном случае пола) определяется инцидентность. У респондентов-женщин инцидентность наступления депрессии равна:
40/(40 + 143)=0,219
У респондентов-мужчин инцидентность равна
10/(10 + 101)=0,09
Отношение инцидентностей составляет
0,219/0,090 = 2,426
и называется относительным риском или мерой относительного риска. Риск попасть в депрессию у женщин в 2,426 раза выше, чем у мужчин. Так как компьютер не знает, какое из двух кодовых значений переменной риска соответствует наличию депрессии, относительный риск вычисляется для обоих значений.
При групповом исследовании применяется несколько отличный вариант коэффициента, называемый также "отношением шансов" (отношением перекрестных произведений). "Шансы" попасть в депрессию у женщин составляют 40/143, а у мужчин — 10/101. Следовательно, отношение шансов равно
(40 * 101)/(143 * 10)= 2,825
Если обозначить четыре частоты в таблице буквами а, Ь, с и d (см. выше), то формулы, которые SPSS использует для вычисления мер риска, можно записать так:
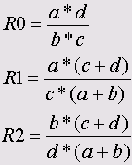
Проведем анализ приведенного примера в SPSS.
-
Загрузите файл depr.sav.
Этот файл содержит переменную риска depr с кодовыми значениями 1 = да и 2 = нет и независимую (причинную) переменную sex с кодовыми значениями 1 = женщины и 2 = мужчины. Еще одна переменная, n, содержит частоты наблюдений.
-
Выберите в меню команды Data (Данные) Weight Cases... (Взвесить наблюдения) и задайте n как переменную взвешивания.
-
В диалоговом окне Crosstabs определите переменную sex как переменную строк и depr — как переменную столбцов, а во вспомогательном диалоге Statistics установите флажок Risk (Риск).
В окне просмотра будут показаны следующие результаты.
Пол * Депрессия Таблица сопряженности
|
Депрессия |
Total | |||
|
|
да | нет | ||
|
Пол | Женщины |
40 |
143 |
183 |
| Мужчины |
10 50 |
101 |
111 | |
|
Total |
244 |
294 | ||
Risk Estimate (Оценка риска)
| Value |
|
95% Confidence Interval (95% доверительный интервал) | |
|
|
Lower (Нижняя граница) | Upper (Верхняя граница) | |
|
Odds Ratio for (Отношение шансов для) Пол (Женщины / Мужчины) | 2,825 |
1,350 |
5,911 |
|
For cohort (Для когорты) Депрессия = да | 2,426 |
1,265 |
4,655 |
|
For cohort (Для когорты) Депрессия = нет | ,859 |
,780 |
,946 |
|
N of Valid Cases | 294 |
|
|
Здесь последовательно показаны отношение шансов (RO) и оба коэффициента относительного риска (R1 и R2). Кроме того, для каждой величины определен 95 % доверительный интервал.
Чтобы правильно вычислить отношение шансов и относительный риск, надо учитывать следующие правила построения таблиц сопряженности:
-
Определяйте причинную (независимую) переменную как переменную строк, а переменную риска — как переменную столбцов.
-
В первой ячейке каждой строки таблицы должна находиться группа с наибольшим риском.
-
В первой ячейке каждого столбца таблицы должно стоять кодовое значение совершения события.
Тест хи-квадрат по Мак-Немару
Тест хи-квадрат по Мак-Немару применяется при наличии двух независимых дихотомических переменных; он рассматривается в разделе 14.2.
Статистика Кохрана и Мантеля-Хзнзеля
Эта статистика включает метод вычисления отношения шансов в таблицах сопряженности 2x2. Расчет этой статистики задается флажком Risk. При вычислениях используется переменная слоев (ковариация) и определяется, значительно ли отличаются категории этой переменной по своему отношению шансов от 1 (или другой величины). Это можно пояснить на примере.
-
Загрузите файл angst.sav.
В этом файле в трех переменных хранятся сведения о 1737 людях: их пол (1 = женский, 2 = мужской), наличие тревожной депрессии (1 = да, 2 = нет) и избыточного веса (1 = нет, 2 = да). Для людей с избыточным весом и с недостатком веса составим раздельные таблицы сопряженности пола и наличия тревожной депрессии, а затем вычислим отношение шансов.
-
Выберите в меню команды Data (Данные) Split File... (Разделить файл)
Выберите опцию Organize output by groups (Разделить вывод на группы) и задайте gewicht как группирующую переменную.
-
Выберите команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
-
Перенесите переменную sex в список переменных строк, а переменную angst — в список переменных столбцов.
-
Кнопкой Cells... (Ячейки) задайте вывод процентов по строкам (Percentages — Row), а кнопкой Statistics... (Статистика) — вывод риска (Risk):
Основная часть результатов приводится ниже.
Пол * Тревожная депрессия Crosstabulation (a)
|
Тревожная депрессия |
Total | ||||
|
|
|
| Да | нет | |
|
Пол |
женский |
Count | 154 |
592 |
746 |
|
% от Пол | 20,6% |
79,4% |
100,0% | ||
|
мужской |
Count | 79 |
715 |
794 | |
|
% от Пол | 9,9% |
90,1% |
100,0% | ||
|
Total |
Count | 233 |
1307 |
1540 | |
|
% от Пол | 15,1% |
84,9% |
100,0% | ||
|
Избыточный вес = нет | |||||
Risk Estimate (a)
| 95% Confidence Interval
| ||||
|
|
Value | Lower | Upper | |
|
Odds Ratio for Пол (женский / мужской) |
2,354 | 1,758 |
3,154 | |
|
For cohort Тревожная депрессия = да |
2,075 | 1,612 |
2,670 | |
|
For cohort Тревожная депрессия = нет |
,881 | ,844 |
,920 | |
|
N of Valid Cases |
1540 | |||
|
а. Избыточный вес = нет | ||||
Пол * Тревожная депрессия Crosstabulation (a)
|
Тревожная депрессия |
Total | ||||
| Да | нет | ||||
|
Пол |
женский |
Count |
22 |
62 |
84 |
|
% от Пол |
26,2% |
73,8% |
100,0% | ||
|
мужской |
Count |
9 |
104 |
113 | |
|
% от Пол |
8,0% |
92,0% |
100,0% | ||
|
Total |
Count |
31 |
166 |
197 | |
|
% от Пол |
15,7% |
84,3% |
100,0% | ||
|
Избыточный вес; = да |
| ||||
Risk Estimate (a)
|
| Value |
95% Confidence Interval | |
|
|
Lower | Upper | |
|
Odds Ratio for Пол (женский / мужской) | 4,100 |
1,776 |
9,468 |
|
For cohort Тревожная депрессия = да | 3,288 |
1,597 |
6,771 |
|
For cohort Тревожная депрессия = нет | ,802 |
,698 |
,921 |
|
N of Valid Cases | 197 |
|
|
а. Избыточный вес = да
В обоих случаях тревожная депрессия у женщин наступает значительно чаще. Отношение шансов для людей с недостатком веса составляет 2,354, а для людей с избыточным весом — 4,100.
Теперь вычислим статистику Кохрана и Мантеля-Хэнзеля.
-
Чтобы отменить разделение на группы, после вызова команд меню Data (Данные) Split File... (Разделить файл) выберите опцию Analyze all cases, do not create groups (Анализировать все наблюдения, не создавать группы).
-
В диалоговом окне Crosstabs задайте gewicht как переменную слоев, во вспомогательном диалоге Statistics снимите флажок Risk и установите флажок Cochran and Mantel-Haenszel statistics (Статистика Кохрана и Мантеля-Гензеля).
-
В поле Test common odds ratio equals (Общее отношение шансов) оставьте значение 1, установленное по умолчанию.
Из полученных результатов ниже приводится только статистика Кохрана и Мантеля-Гензеля.
Test of Homogenity of the Odds Ratio (Тест на гомогенность отношения шансов) Statistics
|
Statistics |
Chi-Squared (Хи-квадрат) |
df |
Asymp. Sig. (2-sided) | |
|
Conditional (Условная независимость) |
Cochran (Кохран) |
44,665 |
1 |
,000 |
|
Mantel-Haenszel (Мантель-Гензель) |
43,724 |
1 |
,000 | |
|
Homogeneity (Гомогенность) |
Breslow-Day (Бреслоу-Дэй) |
1,522 |
1 |
,217 |
|
Tarone (Тарой) |
1,522 |
1 |
,217 | |
Under the conditional independence assumption, Cochran's statistic is asymptotically distributed as a 1 df chi-squared distribution, only if the number of strata is fixed, while the Mantel-Haenszel statistic is always asymptotically distributed as a 1 df chi-squared distribution. Note that the continuity correction is removed from the Mantel-Haenszel statistic when the sum of the differences between the observed and the expected is 0. (При гипотезе условной независимости статистика Кохрана дает распределение, асимптотически приближающееся к распределению хи-квадрат с 1-ой степенью свободы, только при фиксированном количестве слоев, в то время как статистика Мантеля-Хэнзеля при той же гипотезе всегда дает такое распределение. Обратите внимание, что в статистике Мантеля-Хэнзеля опускается коррекция на непрерывность, если сумма разностей наблюдаемых и ожидаемых величин равна 0.)
Mantel-Haenszel Common Odds Ratio Estimate (Оценка общего отношения шансов Мантеля-Гензеля)
|
Estimate (Оценка) |
2,503 | ||
|
ln(Estimate) |
,918 | ||
|
Std. Error of (Стандартная ошибка) In(Estimate) |
,141 | ||
|
Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя) |
,000 | ||
|
Asymp. 95% Confidence Interval (Асимптотический 95 % доверительный интервал) |
Common Odds Ratio (Общее отношение шансов) |
Lower Bound (Нижняя граница) |
1,901 |
|
Upper Bound (Верхняя граница) |
3,297 | ||
|
ln(Common Odds Ratio) |
Lower Bound (Нижняя граница) |
,642 | |
|
Upper Bound (Верхняя граница) |
1,193 | ||
The Mantel-Haenszel common odds ratio estimate is asymptotically normally distributed under the common odds ratio of 1,000 assumption. So is the natural log of the estimate. (Оценка общего отношения шансов Мантеля-Хэнзеля при условии, что общее отношение шансов равно 1,000, имеет асимптотически нормальное распределение. То же распределение сохраняется и для натурального логарифма оценки.)
Результаты тестов Кохрана и Мантеля-Хэнзеля очень близки; в обоих случаях для весовых групп наблюдается максимально значимое отличие отношения шансов от 1 (р<0,001). Тесты как Бреслоу-Дэя, так и Тарона позволяют сохранить допущение о гомогенности отношения шансов для весовых групп (р = 0,217).
Оценка объединенного отношения шансов дает те значения, которые будут получены при вычислении риска, если не разделять данные по переменной слоев.
