11.3.3 Меры связанности для переменных с номинальной шкалой
Коэффициент корреляции нельзя применять в качестве характеристики зависимости между переменными, если эти переменные принадлежат к номинальной шкале и имеют более двух категорий, потому что между их кодировками невозможно установить порядкового отношения и, следовательно, они не могут быть расположены в определенном, рационально объяснимом порядке.
Наилучшим средством для анализа таких зависимостей считается представленный в разделе 11.3.1 тест хи-квадрат, после которого при необходимости можно провести анализ наблюдаемых и ожидаемых частот, а также нормированных остатков. Этот анализ был описан в разделе 8.7.2.
Тем не менее и в этом случае также производились попытки разработать критерии количественной оценки степени связанности двух переменных, поставленных во взаимное соответствие. Эти критерии показывают степень взаимной зависимости или независимости двух переменных, принадлежащих к с номинальной шкале, причем значение 0 соответствует полной независимости переменных, а 1 — их максимальной зависимости. Меры связанности не могут иметь отрицательных значений, так как при отсутствии порядкового отношения нельзя дать ответа на вопрос о направлении зависимости.
В опросе членов городской организации одной из политических партий среди прочего выяснялось их занятие и определялось, выполняет ли респондент какую-либо партийную функцию. Выдержка из ответов респондентов-мужчин содержится в файле partei.sav.
-
Загрузите файл partei.sav и создайте таблицу сопряженности с переменной funk в строках и переменной beruf в столбцах.
-
Задайте вывод ожидаемых частот, стандартизованных остатков, процентов по столбцам и критерия хи-квадрат.
Занятие * Партийная работа Crosstabulation (Таблица сопряженности)
|
Занятие |
Total | ||||||
|
|
|
| Наемный работник |
Государст- венный служащий | Предпри-ниматель | ||
|
Партийная работа |
да |
Count | 13 |
16 |
7 |
36 | |
|
Expected Count | 12,4 |
10,1 |
13,5 |
36,0 | |||
|
% от Занятие | 59,1% |
88,9% |
29,2% |
56,3% | |||
|
Std. Residual | ,2 |
1,8 |
-1,8 |
| |||
|
нет |
Count | 9 |
2 |
17 |
28 | ||
|
Expected Count | 9,6 |
7,9 |
10,5 |
28,0 | |||
|
% от Занятие | 40,9% |
11,1% |
70.8% |
43,8% | |||
|
Std. Residual | -,2 |
-2,1 |
2,0 |
| |||
|
Total |
Count | 22 |
18 |
24 |
64 | ||
|
Expected Count | 22,0 |
18,0 |
24,0 |
64,0 | |||
|
% от Занятие | 100,0% |
100,0% |
100,0% |
100,0% | |||
Chi-Square Tests
|
|
Value |
df |
Asymp. Sig. (2-sided) |
|
Pearson Chi-Square (Критерий хи-квадрат по Пирсону) |
15,01 7 (a) |
2 |
,001 |
|
Likelihood Ratio (Отношение правдоподобия) |
16,421 |
2 |
,000 |
|
Li near-by-Li near Association (Зависимость линейный-линейный) |
4,420 |
1 |
,036 |
|
N of Valid Cases |
64 |
|
|
а. и cells (,0%) have expected count less than 5. The minimum expected count is 11,50. (0 ячеек (,0%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 7,88.)
Результат получился максимально значимым: участие в партийной работе весьма характерно для государственных служащих, а для предпринимателей — совсем не характерно, тогда как наемные работники находятся посредине. Теперь зададим (кнопкой Statistics...) вывод всех мер связанности для переменных, принадлежащих к номинальной шкале (флажки в группе Nominal).
Directional Measures (Направленные меры)
|
|
Value |
Asympt. Std. Error (a) |
Approx. Т (b) |
Approx. sig. | ||
|
Nominal by Nominal (Номиналь- ный-номина- льный) |
Lambda (Лямбда) |
Symmetric (Симметри- ческая) |
,279 |
,104 |
2,554 |
,011 |
|
Партийная работа Dependent (B зависимости от Партийная работа) |
,357 |
,140 |
,211 |
,035 | ||
|
Занятие Dependent (В зависимости от Занятие) |
,225 |
,106 |
1,930 |
,054 | ||
|
Goodman and Kruskal tau (Tay Гудмена-Крускала) |
Партийная работа Dependent |
,235 |
,093 |
|
,001 (c) | |
|
Занятие Dependent |
,116 |
,051 |
|
,001 (c) | ||
|
Uncertainty Coefficient (Коэффициент неопреде- ленности) |
Симметричный |
,144 |
,063 |
2,269 |
,000 (d) | |
|
Партийная работа Dependent |
,187 |
,082 |
2,269 |
,000 (d) | ||
|
Занятие Dependent |
,118 |
,052 |
2,269 |
,000 (d) | ||
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
с. Based on chi-square approximation (На основе аппроксимации по распределению хи-квадрат).
d. Likelihood ratio chi-square probability (Степень правдоподобия при распределении вероятности по закону хи-квадрат).
Symmetric Measures (Симметричные меры)
|
|
Value |
Approx. Sig. | |
|
Nominal by Nominal (Номинальный-номинальный) |
Phi (Фи) |
,484 |
,001 |
|
Cramer's V (V Крамера) |
,484 |
,001 | |
|
Contingency Coefficient (Коэффициент сопряженности признаков) |
,436 |
,001 | |
|
N of Valid Cases |
64 |
| |
a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).
b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).
Коэффициент сопряженности признаков (Пирсона)
Его величина всегда находится в пределах от 0 до 1 и вычисляется (как и значения критериев Фишера (<р) и Крамера (V)) с использованием значения критерия хи-квадрат:
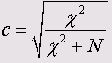
Здесь N — общая сумма частот в таблице сопряженности. Так как N всегда больше нуля, коэффициент сопряженности признаков никогда не достигает единицы. Максимальное значение зависит от количества строк и столбцов таблицы сопряженности и в таблице размером 3*2 составляет (как в данном примере) 0,762. По этой причине коэффициенты сопряженности признаков для двух таблиц с разным количеством полей несопоставимы.
Критерий Фишера (<р)
Этот коэффициент можно использовать только для таблиц 2*2, так как в других случаях он может превысить значение 1:
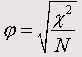
Критерий Крамера (V)
Этот критерий представляет собой модификацию критерия Фишера и для любых таблиц сопряженности он дает значение в пределах от 0 до 1, включая 1:
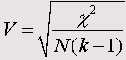
Здесь k — наименьшее из количеств строк и столбцов.
Три названных критерия основаны на использовании критерия хи-квадрат. Они различными способами нормируют его значение по отношению к размеру выборки. Так, если формуле для V Крамера положить k = 2, то значения (р и V Крамера совпадут. Определение значимости основано на значении критерия хи-квадрат.
При оценке полученных значений мер связанности, находящихся в нашем примере в промежутке между 0,4 и 0,5, следует учесть, что значение 1 достигается очень редко или вообще никогда. Другие меры связанности (Я, т Гудмена-Крускала и коэффициент неопределенности) определяются на основе так называемой концепции пропорционального сокращения ошибки. При определении этих критериев одна переменная рассматривается как зависимая; по этой причине данные критерии называются "направленными мерами".
Лямбда
В данном примере вопрос о партийной работе можно рассматривать как зависимую переменную, определяемую родом занятий. Если для какого-то отдельно взятого человека надо сделать предположение о том, выполняет ли он партийную работу или нет, то, естественно, делается наиболее вероятное предположение, соответствующее наиболее часто даваемому ответу — в данном случае, предположение о том, что опрашиваемый занимается партийной работой. Такой ответ дают 56,3% респондентов; однако в 43,7% наблюдений наше предположение будет неверным.
Вероятность предположения можно повысить, если учитывать другую переменную — род занятий. Для наемных работников, как и для государственных служащих, можно достаточно уверенно прогнозировать участие в партийной работе, причем этот прогноз окажется неверным для 9 наемных работников и для 2 государственных служащих. В то же время для предпринимателей можно с большими основаниями предположить, что они не занимаются партийной работой, и ошибиться в 7 наблюдениях. Таким образом, для общего числа 64 опрашиваемых мы получаем 9 + 2 + 7=18 наблюдений, или 28,1 %, в которых прогноз будет неверен. Легко видеть, что первоначальная вероятность ошибки 43,7% значительно сократилась.
На основе этих двух вероятностей можно вычислить относительное сокращение ошибки, которое и называется лямбда:
Лямбда=(Ошибка при первом прогнозе — Ошибка при втором прогнозе)/Ошибка при первом
В нашем примере:
Лямбда =( 43,7% - 28.1%)/43,7% = ,357
Если ошибка при втором прогнозе сокращается до 0, лямбда будет равна 1. Если ошибки при первом и при втором прогнозе одинаковы, лямбда = 0. В этом случае вторая переменная никак не помогает в уточнении предсказания значения первой (зависимой переменной); то есть выбранные две переменные совершенно не зависят друг от друга.
Так как ваш быстрый, но совершенно не умеющий соображать компьютер не знает, какую переменную следует считать зависимой, SPSS вычисляет оба значения Я, поочередно рассматривая каждую из переменных как зависимую. В случае, если выясняется, что ни одну из выбранных переменных нельзя объявить зависимой, выводится среднее двух этих значений с обозначением "лямбда -симметричная".
Тау (т) Гудмена-Крускала
Это вариант меры связанности , который SPSS всегда вычисляет совместно с ней. При определении этой меры количество правильных предсказаний определяется по-иному: наблюдаемые частоты взвешиваются с учетом своих процентов и складываются. Для первого прогноза это дает:
36 * 56,3% + 28 * 43,8% =32,53
Согласно этому выражению, из 64 респондентов неверное предположение сделано для 31,47, что составляет 49,17%.
С учетом второй переменной количество верных предположений (второй прогноз) составляет:
13 * 59,1 % + 16 * 88,9 % + 7 * 29,2 % + 9 * 40,9 % + 2 * 11,1 % + 17 * 70,8 % = 39,89
Итак, при втором прогнозе сделано 24,11 неверных прогнозов из 64, что составляет 37,67%. Тогда сокращение ошибки равно
(49.17 %-37.67%)/49,17 %=0,235
Это значение выводится под названием "тау Гудмена-Крускала". И в этом случае SPSS выдает второе значение т, рассматривая вторую переменную, как зависимую.
Коэффициент неопределенности
Это еще один вариант критерия лямбда, при определении которого имеется в виду не ошибочное предсказание, а "неопределенность", то есть степень неточности предсказаний. Эта неопределенность вычисляется по достаточно сложным формулам, которые мы опускаем. Коэффициент неопределенности также принимает значения в диапазоне от 0 до 1. Значение 1 говорит о том, что одну переменную можно точно предсказать по значениям другой.
