Цель решаемой задачи — выбор лучшего банка для размещения денежных средств физическим лицом. В отличие от предыдущего примера используемые для выбора критерии имеют различную значимость для ЛПР.
Было выбрано три банка: альтернативы а1, а2; и a3.
Определено шесть критериев выбора:
F1 — процентная ставка (этот параметр может меняться для различных условий вклада в данном банке, однако задача будет решаться исходя из предположения, что ЛПР определился с условиями вклада и рассматривает альтернативы, удовлетворяющие этим условиям);
F2 — расположение банка;
F3 — активы банка;
F4 — политика банка;
F5 — ликвидность банка (рассчитывается через коэффициент ликвидности Кл);
f6 — репутация банка (оценивается по экспертной шкале).
Значения критериев для всех альтернатив определены в табл. 4.3.
Таблица 4.3 Значения критериев для альтернатив
|
Критерий
|
Альтернатива
|
||
|
Банк a1
|
Банк a2
|
Банк a3
|
|
|
F1 - процентная ставка, %
|
30
|
35
|
40
|
|
F2- расположение
|
Рядом с домом
|
В одном районе
|
В одном городе
|
|
F3 -активы банка, млн руб.
|
15
|
20
|
10
|
|
F4 - политика банка
|
Консервативная
|
Умеренная
|
Рискованная
|
|
F5 - ликвидность (Кл )
|
2
|
2,5
|
1,5
|
|
F6- репутация (2,3,4,5)
|
5
|
4
|
3
|
Для каждой альтернативы определены конкретные значения, которые представлены следующими нечеткими множествами:






На рис. 4. 4 приведена экранная форма системы принятия решений на нечетких множествах, которая используется для ввода исходной информации о критериях и альтернативах.

Критерии имеют различную значимость при определении наиболее рационального варианта. В связи с этим необходимо определить весовые коэффициенты bi критериев. Один из возможных способов получения значений весовых коэффициентов заключается в построении матрицы попарных сравнений критериев.
Для критериев, использованных при решении задачи выбора лучшего банка, составлена следующая матрица:
|
Выбор банка |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
|
F1 |
1 |
7 |
3 |
4 |
1/4 |
1/3 |
|
F2 |
1/7 |
1 |
1 |
1/2 |
1/7 |
1/2 |
|
F3 |
1/3 |
1 |
1 |
1/2 |
1/4 |
1/2 |
|
F4 |
1/4 |
2 |
2 |
1 |
1/5 |
1 |
|
F5 |
4 |
7 |
4 |
5 |
1 |
3 |
|
F6 |
3 |
2 |
2 |
1 |
1/3 |
1 |
Весовой коэффициент критерия bi определяется на основании вычисленных значений правого собственного вектора матрицы попарных сравнений ai с последующим умножением на число критериев п.
bi = ai n.
Значения ai и bi приведены в табл. 4.4.
Таблица 4. 4 Собственный вектор матрицы полярных сравнений критериев и их весовые коэффициенты

Множество оптимальных альтернатив В с учетом различной важности критериев качества определяется путем пересечения нечетких множеств следующим образом:
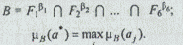
Найдем множество оптимальных альтернатив с учетом полученных весовых критериев:
В = { min { 0,051,062; 0,70,318; 0,350,404; 0,250,589; 0,52,652; 1,00,972 }
min { 0,251,062; 1,00,318; 0,60,404; 0,70,589; 0,92,652; 0,750,972 }
min { 0,41,062; 0,30,318; 0,20,404; 0,30,589; 0,352,652; 0,60,972 }}.
Множество оптимальных вариантов В имеет вид:

Таким образом, лучшей альтернативой является банк а2 на втором месте банк a3 самым худшим вариантом для вклада денег является банк а1.
