На основании приведенных выше исходных данных о критериях и альтернативах экспертом сформулированы правила:
d1 : "Если с1 = ВЫСОКАЯ, и с2 = ХОРОШАЯ, и с3 = ПРИЕМЛЕМЫЕ, то Y = УДОВЛЕТВОРИТЕЛЬНЫЙ";
d2 : "Если c1 = ОЧЕНЬ ВЫСОКАЯ, и c2 = ХОРОШАЯ, и c3 = ПРИЕМЛЕМЫЕ, и c4 = НИЗКИЙ, и c5 = ОЧЕНЬ НИЗКИЙ, то Y = БЕЗУПРЕЧНЫЙ";
d3 : "Если c1 = НИЗКАЯ, и c2 = ПЛОХАЯ, и с3 = ВЫСОКИЙ, то Y = НЕУДОВЛЕТВОРИТЕЛЬНЫЙ".
Переменная Y задана на множестве J = {0; 0,1; 0,2; ...; 1}.
Значения переменной Y заданы с помощью следующих функций принадлежности:
S = УДОВЛЕТВОРИТЕЛЬНЫЙ, mS(x) =х,хÎ J;

US = НЕУДОВЛЕТВОРИТЕЛЬНЫЙ, mUS(x) = 1-х, x Î J. В рассматриваемой задаче оценки инвестиционных проектов заданы следующими нечеткими множествами:
ВЫСОКАЯ (рентабельность) А = {0,5/а1; 0,1/а2; 1/а3};
ОЧЕНЬ ВЫСОКАЯ (рентабельность) 
![]() (a);
(a);
НИЗКАЯ (рентабельность) 
![]() (a);
(a);
ХОРОШАЯ (оценка рынков сбыта) В = {0,7/a1, 0,5/а2, 0,2/a3};
ПЛОХАЯ (оценка рынков сбыта) 
![]() (a)
(a)
ПРИЕМЛЕМЫЕ (первичные средства) G = {0,3/a1, 0,5/a2,1/a3};
НИЗКИЙ (производственный риск) D = {0,5/a1, 0,3/а2, 0,9/a3};
НИЗКИЙ (инвестиционный риск) Е = {0,6/a1, 0,4/а2, 0,2/a3}
ОЧЕНЬ НИЗКИЙ (инвестиционный риск) 
![]() (a);
(a);
ВЫСОКИЙ (инвестиционный риск) 
![]() (a).
(a).
Дополнительные градации лингвистических оценок (со словом ОЧЕНЬ) предназначены для учета наиболее важных критериев. В данном случае это рентабельность (c1) и инвестиционный риск (c5).
С учетом введенных обозначений правила d1, ..., d3 принимают вид:

Функции принадлежности 

Правила приобретут следующий вид:
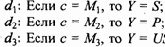
Используя для преобразования правил импликацию Лукасевича, получим нечеткие отношения D1, ... D3 на U x J и в результате их пересечения функциональное решение D:

Для альтернатив вычислены следующие точечные оценки:
F(a1) = 0,500;
F(a2) = 0,431;
F(a3) = 0,600.
Максимальную оценку имеет третья альтернатива, следовательно, она является наиболее предпочтительной.
