Элементы теории нечетких множеств успешно применяются для . принятия решений. Экспертные оценки альтернативных вариантов по критериям могут быть представлены как нечеткие множества или числа, выраженные с помощью функций принадлежности. Для упорядочения нечетких чисел существует множество методов, которые отличаются друг от друга способом свертки и построения нечетких отношений. Последние можно определить как отношения предпочтительности между объектами. Рассмотрим одну из математических постановок задач принятия решений на основе теории нечетких множеств.
В данном случае критерии определяют некоторые понятия, а оценки альтернатив представляют собой степени соответствия этим понятиям.
Пусть имеется множество альтернатив А = {а1, а2, ..., аm,} и множество критериев С= {С1, С2, ..., Сn}, при этом оценки альтернатив по каждому i-му критерию представлены нечеткими множествами:
Сi= {mCi (a1)/ mCi, (a2)/a2, …, mCi (am)/am}
Правило выбора лучшей альтернативы можно представить как пересечение нечетких множеств, соответствующих критериям:
D = С1 Ç C2 Ç ... Ç Сn.
Операция пересечения нечетких множеств может быть реализована разными способами. Иногда пересечение выполняется как умножение, но обычно этой операции соответствует взятие минимума:

Лучшей считается альтернатива a*, имеющая наибольшее значение функции принадлежности

Если критерии Сi имеют различную важность, то их вклад в общее решение можно представить как взвешенное пересечение:
D=C1a1 Ç C2a2Ç ...Ç nan,
где аi - весовые коэффициенты соответствующих критериев, которые должны удовлетворять следующим условиям:
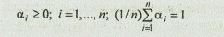
Коэффициенты относительной важности можно определить, используя процедуру попарного сравнения критериев.
