1. Первоначальное распределение объектов по кластерам.
Выбирается число k, и на первом шаге эти точки считаются "центрами" кластеров. Каждому кластеру соответствует один центр.
Выбор начальных центроидов может осуществляться следующим образом:
o выбор k-наблюдений для максимизации начального расстояния;
o случайный выбор k-наблюдений;
o выбор первых k-наблюдений.
В результате каждый объект назначен определенному кластеру.
2. Итеративный процесс.
Вычисляются центры кластеров, которыми затем и далее считаются
покоординатные средние кластеров. Объекты опять перераспределяются.
Процесс вычисления центров и перераспределения объектов продолжается до тех пор, пока не выполнено одно из условий:
o кластерные центры стабилизировались, т.е. все наблюдения принадлежат кластеру, которому принадлежали до текущей итерации;
o число итераций равно максимальному числу итераций.
На рис. 14. 1 приведен пример работы алгоритма k-средних для k, равного двум.
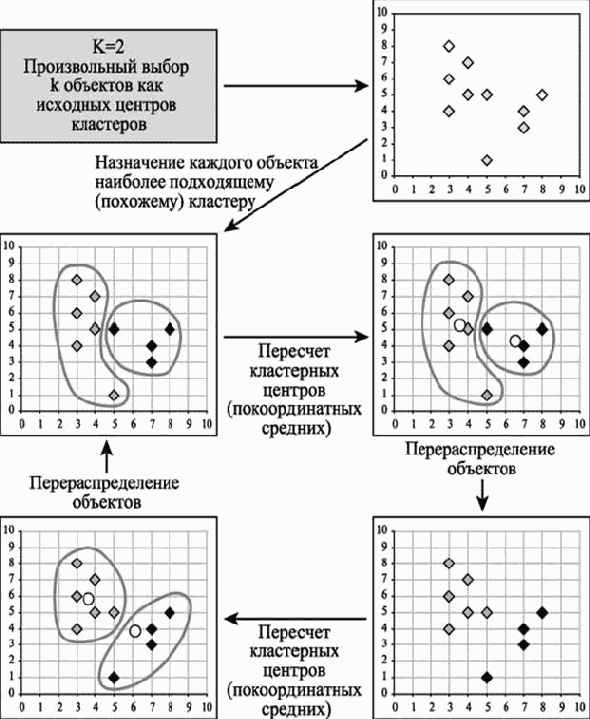
Выбор числа кластеров является сложным вопросом. Если нет предположений относительно этого числа, рекомендуют создать 2 кластера, затем 3, 4, 5 и т.д., сравнивая полученные результаты.
Проверка качества кластеризации
После получений результатов кластерного анализа методом k-средних следует проверить правильность кластеризации (т.е. оценить, насколько кластеры отличаются друг от друга). Для этого рассчитываются средние значения для каждого кластера.
При хорошей Достоинства алгоритма k-средних:
• простота использования;
• быстрота использования;
• понятность и прозрачность алгоритма.
Недостатки алгоритма k-средних:
• алгоритм слишком чувствителен к выбросам, которые могут искажать среднее. Возможным решением этой проблемы является использование модификации алгоритма -алгоритм k-медианы;
• алгоритм может медленно работать на больших базах данных. Возможным решением данной проблемы является использование выборки данных.
