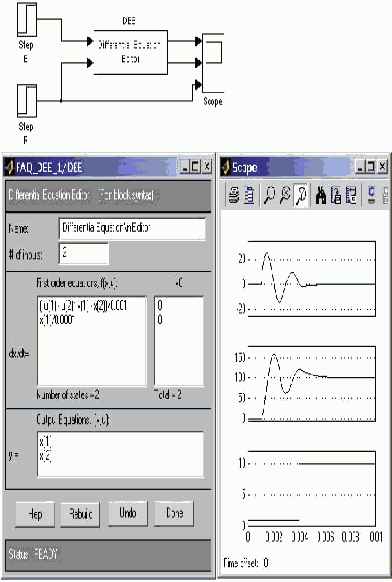
Simulink содержит специальный блок – Differential Equation Editor (редактор дифференциальных уравнений). С помощью этого блока можно задавать системы дифференциальных уравнений в явной форме Коши и выполнять их решение. Вызов редактора выполняется вводом команды dee в окне MATLAB.
Использование редактора рассмотрим на примере расчета переходных процессов в последовательном колебательном контуре. Задача заключается в нахождении тока протекающего в электрической цепи и напряжения на конденсаторе C после замыкания ключа. Начальные условия полагаем нулевыми (ток в цепи отсутствует, и конденсатор не заряжен).
Предварительно составляем систему дифференциальных уравнений, описывающую электрическую цепь:
di e = L + R ⋅ i + udt c duci = C dt
где i – ток в цепи,
uc -напряжение на конденсаторе.
Записываем данную систему уравнений в явной форме Коши:
di e − R ⋅ i − uc = dt L duc 1 =⋅ i dt C
Вводим “машинные” переменные: i→ x(1), uc→ x(2), e→u(1) .
В итоге система уравнений примет вид: dx(1) u(1) − R ⋅ x(1) − x(2)
Введение “машинных” переменных, связано с тем, что редактор дифференциальных уравнений требует задавать в виде векторов входные воздействия (u) и переменные состояния (х) и имена этих векторов жестко заданы.
После получения системы дифференциальных уравнений с использованием “машинных” переменных, необходимо запустить редактор командой dee в окне MATLAB. Затем нужно поместить блок редактора в окно с создаваемой моделью, открыть окно редактора и ввести систему дифференциальных уравнений, начальные условия, а также алгебраические уравнения для расчета выходных сигналов (в рассматриваемой задаче выходные переменные равны переменным состояния). Также необходимо указать размерность вектора входного сигнала (# of inputs). Схема модели и окно редактора показаны на рисунке 10.2. Там же приведены и результаты расчета.
Значения постоянных коэффициентов системы уравнений можно задавать не только как числовые константы, но и использовать переменные рабочей области MATLAB.
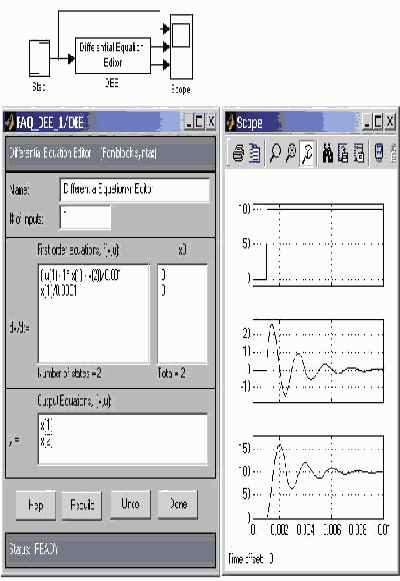
Достоинством редактора DEE является также то, коэффициенты дифференциального уравнения могут быть переменными и задаваться также как и входные сигналы (через входной порт). В качестве примера на рисунке 10.3 показан вариант предыдущей модели, в котором величина сопротивления увеличивается в 10 раза в процессе расчета. В системе дифференциальных уравнений сопротивление записано как входной сигнал u(2).