МОДЕЛЬ БЛЭКА-СКОЛЕСА

а) Определение премии опционов на акции, не выплачивающие дивиденды. Логнормальное распределение. Стандартное отклонение
В начале 70-х годов Ф. Блэк и М. Сколес разработали модель
оценки премии европейских опционов колл и пут для акций, не
выплачивающих дивиденды. Блэк и Сколес вывели формулы, основываясь на концепции формирования портфеля без риска. Они
рассмотрели портфель из акций и опциона. При оценке премии
опциона модель учитывает следующие параметры: цену акции,
цену исполнения, ставку без риска, стандартное отклонение курса
акций, время до истечения контракта. В то же время она не принимает во внимание ожидаемый доход на акции. Данный подход
вытекает из принципа формирования портфеля нейтрального к
риску. В такой ситуации ожидаемый доход на все бумаги является
одинаковым и равняется ставке без риска. Именно она используется для оценки дисконтированной стоимости будущих доходов.
Опционный контракт — это срочный контракт, поэтому величина премии должна уловить поведение курса акции. В качестве
вероятностного распределения цены акции в модели принято логнормальное распределение. Рассмотрим его более подробно.
ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Изменение цены актива в будущем — это случайный процесс,
который в принципе должен описываться нормальным распределением. В то же время для целей вероятностной оценки стоимости
актива в теории пользуются не нормальным, а логнормальным
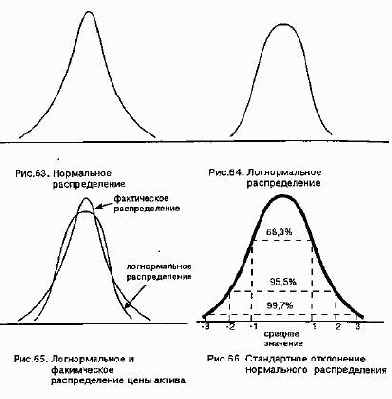
распределением. Это обусловлено следующими причинами. Во первых, нормальное распределение (рис. 63) является симметричной кривой относительно ее центральной оси и может иметь как
положительные, так и отрицательные значения.



Однако, цена актива, лежащего в основе опционного контракта, не может быть отрицательной. Во-вторых, нормальное распределение говорит о равной вероятности для переменной пойти вверх или вниз. В то же время на практике, например, присутствует инфляция, которая
оказывает давление на цены в сторону их повышения. В связи с
этим в моделях определения цены опциона пользуются логнормальным распределением. Кривая логнормального распределения
всегда положительна и имеет правостороннюю скошенность, то
есть она указывает на большую вероятность цены пойти вверх
(рис. 64). Поэтому, если, допустим, цена актива составляет 50
долл., то логнормальное распределение говорит, что опцион пут с
ценой исполнения 45 долл. должен стоить меньше опциона колл
с ценой исполнения 55 долл., в то время как в соответствии с
нормальным распределением они должны были бы иметь одинаковую цену.
Теоретические модели определения цены опциона, как и любые
модели, устанавливают определенные условия, в рамках которых
они функционируют, например, неизменными принимаются
ставка без риска, стандартное отклонение и т.п. В то же время на
практике данные величины подвержены изменениям. Кроме того,
оценивая одни и те же активы, инвесторы, исходя из своих ожидании, оперируют цифрами, которые могут отличаться друг от друга.
Поэтому на практике распределение цены актива определяется не
точной формой логнормального распределения, а чаще принимает
несколько отличную от него конфигурацию, которая имеет более
заостренную вершину и более утолщенные концы, как это представлено на рис. 65. Однако данный факт не умаляет практической
ценности моделей. Опытные трейдеры, зная отмеченные особенности, соответствующим образом корректируют значение цены
опциона. Так, например, премия опциона с большим проигрышем
на практике будет оцениваться инвестором несколько дороже, чем
это предлагает модель, построенная на логнормальном распределении.
СТАНДАРТНОЕ ОТКЛОНЕНИЕ
Важным элементом, который присутствует в моделях оценки
премии опционов, является стандартное отклонение. Поэтому остановимся на этом вопросе несколько подробнее.
Вкладчика, инвестирующего свои средства в опционные контракты, интересует не только направление движения рынка, но и
скорость этого движения, поскольку от нее зависит вероятность
того, что стоимость актива перешагнет за цену исполнения опциона.



Показателем такой скорости выступает стандартное отклонение цены актива или, как его еще именуют, волатильность.
Стандартное отклонение говорит о вероятности цены принять то
или иное значение. Оно задает Меру рассеянности цены актива.
Большое значение стандартного отклонения свидетельствует о
том, что цена актива может колебаться в широком диапазоне.
Стандартное отклонение характеризует риск, связанный с данным
активом. Чем больше величины отклонения, тем больше риск, и
наоборот. Стандартное отклонение задается как процент отклонения цены актива от ее средней величины в расчете на год. Например, если цена актива составляет 100 долл., а стандартное
отклонение равно 10%, то это означает, что через год цена его
может лежать в пределах от 90 долл. до 11О долл. (100±10%) в б8,3%
случаев, от 80 долл. до 120 долл. (100±2х10%) в 95,4% случаях и от
70 долл. до 130 долл. (100±3х10%) в 99,7 случаях.

Поскольку цена актива через год представляет собой результат действия рыночных сил, то она может и выйти за указанные пределы, однако в соответствии с кривой нормального распределения 99,7% всех вероятных исходов лежат в пределах трех стандартных отклонений от

среднего значения показателя, 95,4% — в пределах двух стандартных отклонений и 68,3% — одного стандартного отклонения (см.

рис. 66).

Чтобы получить стандартное отклонение за период меньше

года, необходимо стандартное отклонение в расчете на год разделить на квадратный корень из числа данных торговых периодов в

году.

Пример. Стандартное отклонение бумаги равно 10% в год. Необходимо определить стандартное отклонение в расчете на день.

В году насчитывается порядка 252 торговых дней. Поэтому стандартное отклонение за один день равно:

% 63 , 0 252 : % 10 =

Если цена составляет 100 долл., то одно стандартное отклонение

цены за день составит:

100×0,0063 = 0,63 долл.

На практике для расчета стандартного отклонения берут значения котировочной цены. Западные аналитические компании, предоставляющие информацию о стандартном отклонении,

рассчитывают его обычно на основе ежедневных значений котировочной цены.

Формируя свои стратегии, инвестор пытается предугадать будущее значение стандартного отклонения. В этом вопросе он ориентируется в первую очередь на фактические значения стандартного

отклонения за истекший период времени, как минимум за последний год. Помимо общего стандартного отклонения за год его

интересует стандартное отклонение и за более короткие периоды.

Если он планирует заключить опционный контракт на небольшой

срок, то для него важна также информация о стандартном отклонении за последний короткий период. Например, стандартное

отклонение актива за год составило в среднем 20%, а за последний

месяц 10%. Если инвестор планирует купить (продать) опцион на

длительный период, то в расчетах ему следует учесть стандартное

отклонение, равное 20%, если же он заключает контракт на недалекую перспективу, то значение отклонения в пределах от 20% до

10%, скажем, 15%, будет более верным, чем