БИНОМИНАЛЬНАЯ МОДЕЛЬ ДЛЯ АКЦИЙ, ВЫПЛАЧИВАЮЩИХ ДИВИДЕНДЫ
В основе опциона могут лежать акции, на которые в течениедействия контрактов выплачиваются дивиденды. Данный факт
должен найти отражение в некоторой корректировке премии опциона.
Информация о дивиденде может быть задана в двух видах, а
именно, инвестор знает: а) величину ставки дивиденда; б) абсолютный размер предполагаемого дивиденда. Рассмотрим последовательно оба случая.
Как известно, курс акций на дату учета падает на величину
выплачиваемого дивиденда. Поэтому дере во распределения цены
акции принимает вид, как это представлено на рис. 6Данный
рисунок сделан для случая, когда нам известна ставка дивиденда.
Начиная с даты учета, и для всех последующих точек пересечения
ветвей дерева курс акций корректируется на величину 1 - q. Если в
течение действия опционного контракта дивиденд выплачивается
несколько раз, то данная корректировка производится соответствующее число раз. В остальном техника определения цены опциона сводится к уже рассмотренной выше схеме для акций, не
выплачивающих дивиденд.
Инвестор может располагать данными об абсолютном размере
предполагаемого дивиденда. Соответственно на дату учета стоимость акций понизится на данную величину. Теперь сделаем
допущение, что цена акции в каждый момент состоит из двух
частей, а именно, чистой цены, то есть цены без дивиденда, и
приведенной стоимости будущего дивиденда. После данной посылки для определения премии опциона можно воспользоваться построением дерева как и для акций, не выплачивающих дивиденды.
В расчетах значение стандартного отклонения курса акции
берется для ее чистой цены. Значение цены акции в каждой точке
пересечения ветвей дерева, за исключением даты учета, представляет собой сумму ее чистой цены и приведенной стоимости дивиденда для соответствующего момента времени.
Пример. Инвестор планирует купить американский опцион пут
сроком на четыре месяца, цена акции — 48 долл., цена исполнения — 45 долл., стандартное отклонение цены акции — 35%,
ставка без риска — 10%. Дата учета наступает через три месяца,
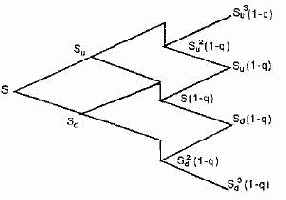
дивиденд равен 3 долл. Определить премию опциона.
В качестве первого шага рассчитаем приведенную стоимость
дивиденда для момента заключения контракта.
3e-0,1х0,25= 2,93 долл.
Чистая цена акции в этот момент составит:
48 долл. -2,90 долл. = 45,07 долл.
Вероятность повышения и понижения курса акции составит как
и в рассмотренном выше примере для акций, не выплачивающих
дивиденды, соответственно 0,5163 и 0,4837, и = 1,1063, d = 0,9039.
Чистая цена акции в точке Su (конец интервала Δt1) равняется:
45,07 долл. × 1,1063 = 49,86 долл.
Приведенная стоимость дивиденда: 3 е -0.1x0,1667= 2,95 долл.
Полная цена в этой точке: 49,86 долл. + 2,95 = 52,81 долл.
Чистая цена акции в точке Su (конец периода Δt2 ) составит:
45,07 долл.× 1,10632 = 55,16 долл.
Приведенная стоимость дивиденда равна:
3е-0,1x0,0833= 2,98 долл.
Курс акции в этой точке равен:
55,16 дол. + 2,98 долл. = 58,14 долл.
В точке Su3 курс акции составит:
45,07 долл.× 1,10633 = 61,02 долл.
К данной цене дивиденд не прибавляется, так как в этот день он
выплачивается акционерам. Цена акции в точке Su4 составит 67,5
долл. Даже если предположить, что через несколько месяцев на
акцию будет выплачен дивиденд, корректировка курса акций на
приведенную стоимость дивиденда не производится, так как
контракт заключен на четыре месяца, и, следовательно, выплата
следующего дивиденда лежит уже за рамками данного опциона.
Аналогичным образом, как представлено выше, рассчитывается
цена акций для каждой точки пересечения ветвей дерева (см.
рис. 62).
Необходимо обратить внимание читателя на точку Sd3. Согласно расчетам, цена опциона должна составлять в этот момент 11,34
долл. Однако, поскольку это американский опцион, он может быть
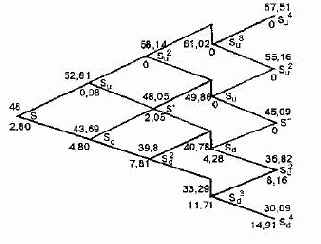
Рис.62. Дерево распределения цены акции и премии американского опциона пут для акций, выплачивающих известный дивиденд. Верхние
числа — курс акции, нижние — премия опциона
исполнен в любой момент времени и, соответственно, цена его
составит 11,71 долл. Равным образом сказанное выше относится и
к точке Sd (конец интервала Δt3 , в которой цена опциона должна
составлять 4,28 долл. Используя технику расчета, о которой говорилось в примере с акциями, не выплачивающими дивиденды,
получаем значение цены опциона пут для момента заключения
контракта 2,80 долл.
Как уже было отмечено в начале данной главы, биноминальная
модель используется для оценки премии американских опционов.
Премии европейских опционов рассчитываются с помощью аналитических формул, которые мы рассмотрим в следующем пара-
графе.
Содержание раздела
