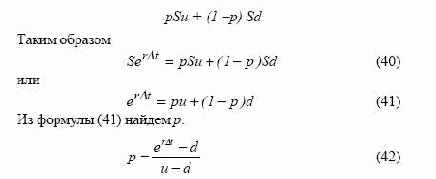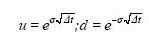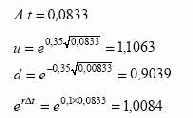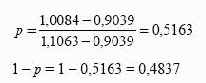БИНОМИНАЛЬНАЯ МОДЕЛЬ ДЛЯ АКЦИЙ, НЕ ВЫПЛАЧИВАЮЩИХ ДИВИДЕНДЫ
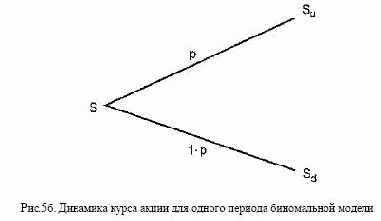
Весь период действия опционного контракта разбивается наряд
интервалов времени, в течение каждого из которых курс акции S
может пойти вверх с вероятностью p или вниз с вероятностью 1-р,
как показано на рис. 56. В конце периода акция соответственно
стоит Su или Sd, где и — процент прироста курсовой стоимости
акций, поэтому и > 7, a d — процент падения курсовой стоимости,
то есть d < 1.
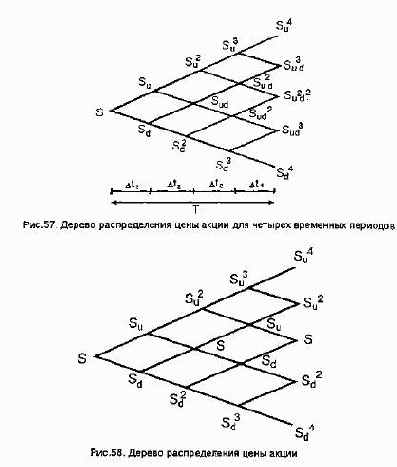
Рассматривая динамику курса акций на каждом временном интервале, можно построить дерево распределения цены акции для
всего периода действия опционного контракта. Данная картина
представлена на рис. 57. Начальная цена акции равна S. За первый
период Δt1 ее курс может составить Su или Sd. За второй период
Δt2 — соответственно Su2, Sd2 или Sud и т.д. для следующих
периодов. В целях упрощения модели, поскольку период действия
опционного контракта делится на большое число интервалов, делается допущение, что u=1/d , поэтому значения курса акций на
дереве распределения можно представить следующим образом (см.
рис. 58).
Как известно, к моменту истечения срока действия контракта
цена опциона может принимать два значения, а именно, 0 или
P-X для опциона колл. и 0 или X-Р для опциона пут. Для того,
чтобы рассчитать стоимость опциона в начале периода 7, необходимо определить стоимость опциона для начала каждого периода
Δt , то есть в каждой точке пересечения ветвей дерева. Данную
задачу решают последовательным дисконтированием. Так, известную величину опциона в конце периода Т дисконтируют, чтобы
получить ее значение в начале периода Δt4. Затем значение опциона в начале периода Δ t4 дисконтируют и определяют его стоимость в начале периода Δ t3 и т.д.
Биноминальная модель основывается на концепции формирования портфеля без риска. Поэтому для дисконтирования принимается процент, равный ставке без риска для инвестиций,
соответствующих времени действии опционного контракта. Для
того, чтобы упростить модель, вместо указанной выше ставки используем эквивалентную ей ставку непрерывно начисляемого процента.
В условиях отсутствия риска ожидаемый доход на акцию за
период At должен составить Se гΔt , где r — непрерывно начисляемая ставка без риска. В то же время, исходя из значения математического ожидания, он должен быть равен:
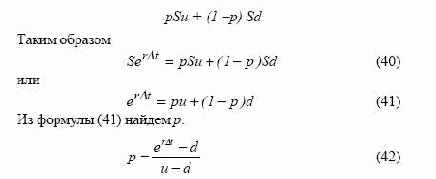
Процент прироста или падения курсовой стоимости акции зависит от времени, в течение которого наблюдается изменение
курса бумаги, и ее стандартного отклонения. Поэтому можно записать, что
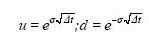
Формула (42) позволяет определить вероятность повышения
или понижения курса акций.
Пример. Курс акции в начале периода равен 40 долл., стандартное отклонение цены акции 35%, непрерывно начисляемая ставка
без риска 10%. Определить вероятность повышения и понижения
курса акций через месяц.
Получаем
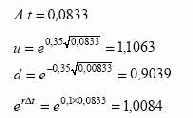
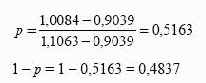
Таким образом, вероятность повышения курса акции через один
месяц составляет 0,5163 и понижения 0,4837.
После того как мы рассчитали значения u и d, можно определить
значение курса акции для любого периода времени. Предположим, что инвестора интересуют возможные значения курса акций
последовательно через один, два и три месяца, то есть для каждой
точки пересечения ветвей дерева, представленного на рис. 58. Для
точки Sd он равен Sd= 40 долл. х 0,9039 = 36,16 долл.
Для точки Sd2 Sd2 = 40 долл. х (0,9039)2 = 32,68 долл.
Для точки Su Su = 40 долл. х 1,1063 = 44,25 долл.
и т.д.
Значения курса акций представлены на дереве распределения
(см. рис. 59).
После того как мы получили значения вероятности повышения
я понижения курса акции и значения цены акции в конце каждого
месяца, можно перейти к определению величины премии опциона.

Пример. Инвестор приобретает опцион пут на три месяца, курс
акции в момент заключения контракта равен 40 долл., цена исполнения 45 долл., непрерывно начисляемая ставка без риска — 10%,
стандартное отклонение акции — 35%. Определить стоимость
опциона.
Через три месяца в точке Su3 величина премии опциона будет
равняться нулю. В точке Su = 45 долл - 44,25 долл., = 0,75 долл.
В точке Sd = 45 долл. - 36,16 долл. = 8,84 долл.
В точке Sd3 = 45 долл. -29,54 долл. = 14,46 долл.
Цена опциона в начале периода Δt3, то есть для точек Su2, S, Sd2
представляет собой дисконтированную стоимость его ожидаемой
цены в конце этого периода и так далее для каждого предыдущего
отрезка времени. Ожидаемое значение случайной величины определяется как ее математическое ожидание. Поэтому цену опциона
в начале периода Δt можно определить по формуле
цена опциона = (Мх) е-rΔT
где Мх — сумма произведения ожидаемых значений цены оп-
циона в конце периода Δt на их вероятность.
Найдем цену опциона в точке Su2. Она равна:
(0,5163 × 0 + 0,4837 × 0,75) е-0,1 ×0,0833 = 0,36 долл.
Для точки S она составит:
(0,5163 × 0,75 + 0,4837 × 8,84) е-0,1 ×0,0833 = 4,62 долл. и т.д.
Цена опциона для каждой точки на дереве распределения представлена второй строкой на рис. 59. В итоге получаем — премия
опциона в начале периода Гравна 5 долл.
Выше мы определили премию для европейского опциона пут.
Рассмотрим теперь случай, когда инвестор покупает аналогичный
по своим условиям американский опцион. Как известно, досрочное .исполнение контракта может явиться оптимальным решением. Поэтому для каждого момента времени (в нашей модели это
конец каждого периода Δt) его цена должна быть не меньше, чем X
- Р. Дерево распределения цены акции и премии американского
опциона приведено на рис. 60. Рассмотрим цену опциона в точке
Su2. Согласно расчету она составляет 0,36 долл. Однако в случае
исполнения опциона в данный момент он будет стоить:
45 долл. — 48,96 долл. = -3,96 долл.
Естественно, что в этот момент времени исполнение опциона
не является оптимальной стратегией и инвестору следует продать
опцион или подождать еще некоторый период времени. Следовательно, его цена в указанной точке равна полученной расчетной
величине, то есть Для точки S (начало периода Δt3) расчетная цена равна 4,62
долл., однако в случае его исполнения в этот момент инвестор
получит прибыль, которая составит:
45 долл. - 40 долл. = 5 долл.
Следовательно, при таком развитии событий американский опцион будет стоить не 4,62 долл, а 5 долл. и его оптимально исполнить. Для точки Sd2 премия опциона должна быть не меньше чем:
45 долл. - 32,68 долл. = 12,32 долл.
Для точки Sd при немедленном исполнении опцион стоит:
45 долл. -36,1бдолл.= 8,84долл.
Его расчетная цена составляет:
(0,5163 × 5,0 + 0,4837 × 12,32) е-0,1 ×0,0833 =8,47 долл.
Следовательно, он должен стоить не меньше 8,84 долл.
В точке Su при немедленном исполнении опцион стоит:
45 долл. - 44,25 долл. = 0,75 долл.
Однако расчеты показывают, что в этом случае исполнение не
является оптимальной стратегией и цена опциона должна составить не 0,75 долл., а
(0,5163 × 0,36 + 0,4837 × 5,0) е-0,1 ×0,0833 = 2,58 долл
В итоге получаем — цена американского опциона пут в момент
заключения контракта равна 5,56 долл.
Мы рассмотрели биноминальную модель оценки премии опциона для акций, не выплачивающих дивиденды. В нашем примере
весь период опционного контракта, который насчитывал три месяца, был разбит на три периода. На практике для определения
цены опциона период Т необходимо разбить на большее число
периодов Δt. Обычно деление опционного контракта на 30-50
интервалов дает приемлемый результат.
Содержание раздела