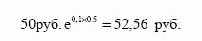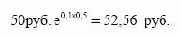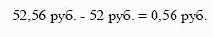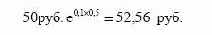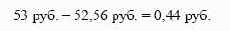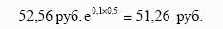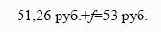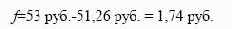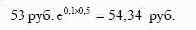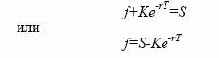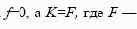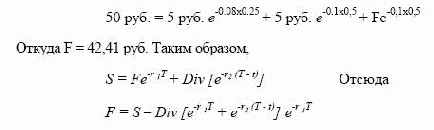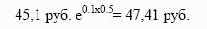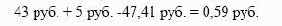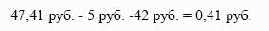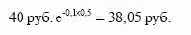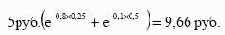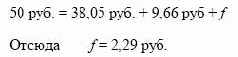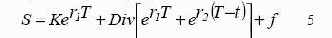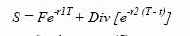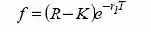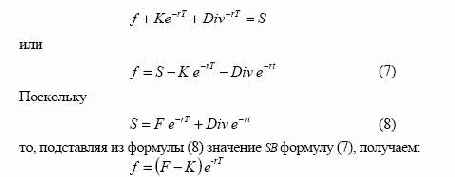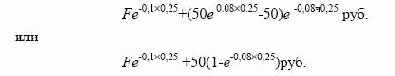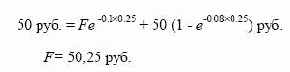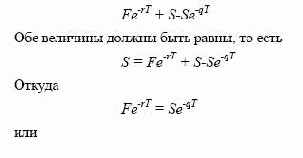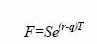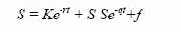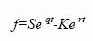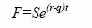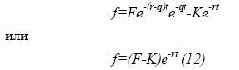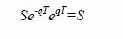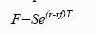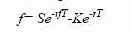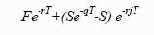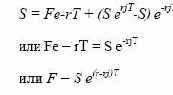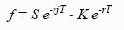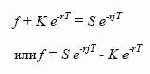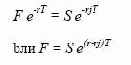ЦЕНА ПОСТАВКИ, ФОРВАРДНАЯ ЦЕНА, ЦЕНА ФОРВАРДНОГО КОНТРАКТА
В момент заключения форвардного контракта стороны согласовывают цену, по которой сделка будет исполнена. Данная цена
называется ценой поставки. Она остается неизменной в течение
всего времени действия форвардного контракта. Цена поставки
является результатом согласования позиций контрагентов. Если
через некоторое время заключается новый форвардный контракт,
то в нем фиксируется новая цена поставки, которая может отличаться от цены поставки первого контракта, поскольку изменились ожидания инвесторов относительно будущей конъюнктуры
рынка для актива, лежащего в основе контракта.
В связи с форвардным контрактом возникает еще одно понятие
цены, а именно, форвардная цена. Для каждого момента времени
форвардная цена — это цена поставки, зафиксированная в форвардном контракте, который был заключен в этот момент. Таким
образом, в момент заключения контракта форвардная цена равна
цене поставки. При заключении новых форвардных контрактов
будет возникать и новая форвардная цена.
Пример. 1 сентября заключен форвардный контракт на товар А
с ценой поставки 100 руб. Таким образом, в этот момент форвардная цена равна цене поставки и составляет 100 руб. Допустим
теперь, что 20 сентября был заключен новый форвардный контракт
на товар А с ценой поставки, равной 120 руб., срок которого
истекает одновременно с первым контрактом. В этом случае цена
поставки для первого контракта остается равно 100 руб., но форвардная цена для данного товара составляет уже 120 руб.
Как мы отметили выше, цена поставки является фиксированной
величиной на протяжении всего времени действия контракта.
Форвардная цена будет меняться в зависимости от конъюнктуры
рынка, то есть в зависимости от ожиданий контрагентов относительно будущей цены спот на данный актив. Когда стороны заключат контракт, форвардная цена равна цене поставки. Открывая
свои позиции, контрагенты не несут никаких расходов. Предположим теперь, что через некоторое время один участник контракта
решил перепродать свои обязательства другому лицу. В данный
момент на рынке установилась уже новая форвардная цена. Естественно предположить, что в зависимости от существующей в момент продажи форвардной цены наш контракт уже будет иметь
некоторую цену, поскольку он дает возможность инвестору получить актив по цене поставки, отличной от цены поставки контрактов, заключаемых в данный момент времени. Ответим на
вопрос, сколько должен стоить в этом случае первый форвардный
контракт. Вначале рассмотрим данный вопрос для активов, на
которые инвестору не выплачивается какой-либо доход в течение
действия контракта.
а) Форвардная цена и цена форвардного контракта на активы,
не выплачивающие дохода
В качестве примера рассмотрим форвардный контракт на акции.
Мы берем акции как более удобный инструмент для объяснения
техники определения форвардной цены и цены форвардного
контракта. В реальной практике форвардные контракты на акции
встречаются редко. Другим примером может служить контракт, в
основе которого лежит облигация с нулевым купоном. В первую
очередь следует ответить на вопрос, чему должна равняться
цена поставки, то есть форвардная цена в момент заключения
контракта.
Допустим инвестор заключает форвардный контракт на поставку через полгода акции компании А. В момент заключения соглашения цена спот акции равна 50 руб., непрерывно начисляемая
ставка без риска 10%. В нашем случае инвестор имеет возможность
купить акцию сейчас за 50 руб. или по некоторой цене через
полгода. С точки зрения его финансовых затрат выбор первого или
второго варианта действий должен быть для него равнозначен. В
противном случае он может совершить арбитражную операцию и
получить доход. Таким образом, 50 руб. сегодня должны представлять собой не что иное, как дисконтированную стоимость будущей
цены акции, которую инвестор согласен заплатить через шесть
месяцев. В качестве процента дисконтирования берется ставка без
риска. Другими словами, инвестор может не покупать сегодня
акцию за 50 руб., а инвестировать эти средства на полгода под
ставку без риска и получить требуемую сумму для приобретения
акции через шесть месяцев. Таким образом, заключая фьючерсный контракт, в качестве цены поставки инвестор установит цену,
которая равна:
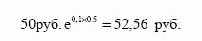
Если цена поставки/форвардная цена будет отличаться отданной величины, то вкладчик совершит арбитражную операцию.
Возможны два случая.*
I. Допустим, что форвардная цена равна 52 руб. Тогда вкладчик
занимает акцию у брокера, продает ее и инвестирует полученные
средства под ставку без риска. Одновременно он покупает форвардный контракт, в соответствии с которым обязуется заплатить
через полгода за акцию 52 руб. Через шесть месяцев он получит
сумму денег, равную:
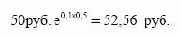
Заплатит 52 руб. за приобретение акции по контракту, вернет ее
брокеру и получит прибыль в размере:
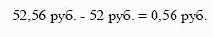
Предположим теперь, что форвардная цена завышена и составляет 53 руб. Тогда инвестор продает форвардный контракт и
покупает акцию, заняв на полгода средства под процент без риска.
Через шесть месяцев вкладчик поставляет акцию по контракту и
получает 53 руб. Он возвращает взятый кредит в размере:
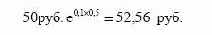
и получает прибыль:
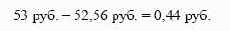
Предположим теперь, что через три месяца покупатель решил
продать свой контракт. Цена акции в момент продажи контракта
равна 53 руб., цена поставки составляет 52,56 руб. Необходимо
ответить на вопрос, сколько стоит контракт.
В соответствии с условием контракта его новый владелец через
три месяца должен будет заплатить за акцию 52,56 руб. Эта цена
эквивалентна сегодня сумме, равной
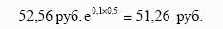
Таким образом, инвестировав 51,26 руб. и купив по некоторой
цене контракт, инвестор сможет получить через три месяца акцию.
В то же время он может купить акцию сегодня за 53 руб. Поэтому,
если цену форвардного контракта обозначить через f, должно выполняться уравнение (3), чтобы исключить возможность арбитражной операции и сделать инвестора безразличным к выбору
первой или второй стратегии:
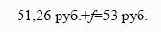
Цена контракта равна:
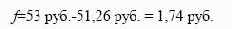
Таким образом, цена форвардною контракта равна разности
между ценой спот акции в момент продажи контракта и приведенной стоимости цены поставки. Данную цену можно найти также
иным путем. Новая, то есть текущая форвардная цена, для контрактов, которые заключаются в момент продажи первого контракта,
должна составлять:
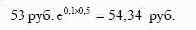
Полученная величина должна равняться сегодня цене поставки,
зафиксированной в первом контракте, плюс будущая стоимость
форвардного контракта к моменту его истечения, то есть:

Таким образом, можно сказать, что цена форвардного контракта равна приведенной стоимости разности между текущей форвардной ценой и ценой поставки. При нарушении данного условия
возникает возможность совершить арбитражную операцию. Если
в нашем случае форвардный контракт будет стоить больше, чем
1,74 руб., то инвестор продаст контракт и купит акцию. Если цена
контракта меньше 1,74 руб., то инвестор купит контракт и продаст
акцию.
Докажем выведенные выше формулы в более общей форме.
Предположим, имеется два портфеля А и Б. Портфель А состоит
из одного длинного форвардного контракта, который стоит f и
суммы денег, равной приведенной стоимости цены поставки акции, то есть Ке -rT , где К — цена поставки. Портфель Б состоит из
одной акции, цена спот которой равна S. По прошествии времени
Т портфель Б будет состоять из одной акции. В портфель А также
войдет одна акция, поскольку величина Ке-rT за период времени Т
возрастет до К. Данная сумма денег используется для приобретения акции по форвардному контракту. Таким образом, стоимость
портфелей А и Б равна в конце периода Т. Следовательно
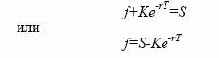
Поскольку в момент заключения контракта
форвардная цена, то
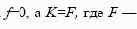
б) Форвардная цена и цена форвардного контракта на активы,
выплачивающие доходы
Определим форвардную цену и цену форвардного контракта на
активы, выплачивающие известный доход в течение действия
контракта. В качестве примера могут служить акции или купонные
облигации.

Пример. Цена спот акции равна 50 руб. Через три и шесть месяцев на нее выплачиваются дивиденты по 5 руб. Непрерывно начисляемая ставка без риска на три месяца — 8 %, на шесть месяцев —
10%. Необходимо определить форвардную цену и цену форвард-
ного контракта, исполнение которого наступит через шесть месяцев. Инвестор имеет две альтернативы: приобрести акцию сейчас
или через полгода, купив сегодня форвардный контракт. Если он
выберет первую стратегию, то получит два дивидента и будет располагать акцией. Чтобы получить точно такой же результат по
второй стратегии, он должен инвестировать сегодня приведенную
стоимость цены поставки и двух дивидентов и купить форвардный
контракт: таким образом, цена спот акции сегодня должна равняться сумме приведенных стоимостей цены поставки и дивидентов, т.е.:
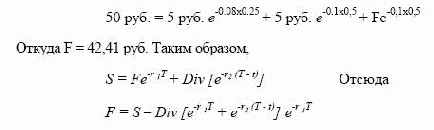
Если форвардная цена отличается от найденной величины, то
возникает возможность совершить арбитражную операцию. Допустим, F=43 руб. Тогда инвестор продает форвардный контракт и
покупает акцию, заняв 50 руб.
Из данной суммы он занимает 5 руб. e-0.08х0.25 = 4,9 руб. на три
месяца под 8%, чтобы возвратить эту часть долга с помощью первого дивиденда. Оставшуюся сумму 45,1 руб. он занимает на полгода под 10%. Через шесть месяцев он должен вернуть
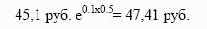
К этому моменту времени инвестор получает второй дивиденд и
цену поставки и возвращает долг. Ею прибыль от операции равна:
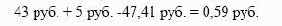
Допустим теперь, что F = 42 руб. В этом случае арбитражер
занимает у брокера акцию, продает ее за 50 руб. и покупает форвардный контракт. Поскольку вкладчик занял у брокера акцию, то
он должен выплатить ему дивиденды, которые выплачиваются
компанией на эту бумагу в течение действия контракта. Поэтому
из полученных 50 руб. вкладчик инвестирует 4,9 руб. на три месяца
под 8%, чтобы за счет этой суммы выплатить первый дивиденд.
Оставшиеся 45, 1 руб. он инвестирует на шесть месяцев под 10%. В
конце действия контракта он выплачивает второй дивиденд, платит 42 руб. за акцию и возвращает ее брокеру. Прибыль по данной
сделке составляет:
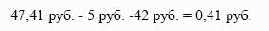
После того как мы рассмотрели технику определения форвардной цены, перейдем к расчету цены форвардного контракта, когда
он покупается на вторичном рынке. Допустим, что до истечения
контракта остается шесть месяцев, через три и шесть месяцев будут
выплачены дивиденды по 5 руб. Контракт был заключен некоторое
время назад и продается в настоящий момент. Цена поставки равна
40 руб., цена спот акции составляет 50 руб. Ставка без риска на три
месяца 8% и шесть месяцев 10%. Необходимо определить стоимость форвардного контракта.
Как мы уже нашли выше, для указанных условий в момент
покупки контракта текущая форвардная цена составляет 42,41 руб.
Инвестор имеет две альтернативы.
I. Купить акцию сейчас за 50 руб., в этом случае в течение
последующих шести месяцев он получит два дивиденда.
II. Купить форвардный контракт на поставку акции через шесть
месяцев по цене 40 руб. В этом случае он не получит двух дивидендов. Чтобы инвестор был безразличен к выбору первого и второго
варианта, они должны быть для него одинаковыми с финансовой
точки зрения. По второму варианту он заплатит через полгода 40
руб. Следовательно, в момент покупки контракта эта сумма эквивалентна величине:
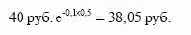
Приведенная стоимость дивидендов к моменту покупки контракта составляет:
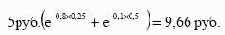
Другими словами, вкладчик может не покупать акцию, чтобы
получить дивиденды, а инвестировать сегодня 9,66 руб. на три и
шесть месяцев под 8% и 10% соответственно. В этом случае он
получит доход, эквивалентный сумме дивидендов.
При первой стратегии к концу шестимесячного периода инвестор будет располагать акцией. По второму варианту инвестор
будет располагать акцией к этому моменту времени, если сегодня
купит форвардный контракт по некоторой цене f.
Таким образом, чтобы через шесть месяцев располагать акцией и дивидендами, по
первой стратегии инвестор должен заплатить сегодня 50 руб. Чтобы через шесть месяцев располагать акцией и доходами, эквивалентными двум дивидендам по второй стратегии, вкладчик должен
инвестировать приведенную стоимость цены поставки, то есть
38,05 руб., приведенную стоимость будущих дивидендов, то есть
9,66 руб., и заплатить за контракт цену f. Сумма инвестиций для
обоих вариантов должна быть одинаковой, иначе возникает возможность совершить арбитражную операцию, то есть
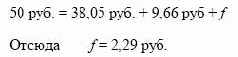
Если цена контракта будет больше 2,29 руб., то арбитражер
продаст контракт и купит акцию. Если цена контракта меньше 2,29
руб., то он продаст акцию и купит контракт.
Запишем полученный выше результат в общем виде:
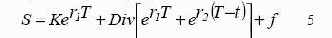
где Г= 6 месяцев, t = 3 месяца. В момент заключения контракта f=0 и K=F, поэтому для этого момента
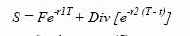
Подставив значение S в формулу (5), получим:
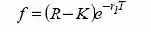
Мы пришли к тому же выводу, который сделали при рассмотрении первого примера, а именно: цена форвардного контракта равна приведенной стоимости разности текущей форвардной цены и
цены поставки. Для нашего примера она равна:

Приведем теперь более строгое доказательство полученного
выше результата. Допустим, имеется два портфеля А и Б. В портфель А входит длинный форвардный контракт на приобретение
акции, выплачивающей дивиденд, сумма денег, равная приведенной стоимости цены поставки Ке-FT, которая инвестируется на
период Т под процент r, и сумма денег, равная приведенной стоимости дивиденда Div e-rT , которая также инвестируется под процент r на период времени t (t<=T и представляет собой момент
выплаты дивиденда на акцию).
В портфель Б входит одна акция. К концу периода Т портфель А будет состоять из акции и суммы денег, равной дивиденду. За этот период времени величина Ке-rТ превратилась в К и была использована на приобретение акции, а сумма Div e-rT стала равна величине дивиденда.
Портфель Б также будет состоять из акции и выплаченного на
нее дивиденда Div. Поскольку стоимости двух портфелей равны к
концу периода Г, то в начале этого периода они также должны быть
равны, чтобы исключить возможность арбитражной операции.
Поэтому можно записать, что
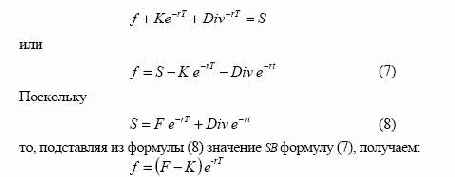
в) Форвардная цена и цена форвардного контракта на акции,
для которых известна ставка дивиденда
В расчетах инвестор может пользоваться не только значением
абсолютной величины выплачиваемого на акции дивиденда, но
также и таким показателем, как ставка дивиденда, которая представляет собой отношение дивиденда к цене акции. В соответствии
с принятым выше порядком мы рассматриваем в наших примерах
ставку дивиденда как непрерывно начисляемую. С теоретической
точки зрения это означает, что дивиденд начисляется и постоянно
реинвестируется на очень короткие промежутки времени. Если
инвестор имеет данные о ставке дивиденда в расчете на год, то по
формуле (1) он легко может пересчитать его в непрерывно начисляемый дивиденд.
Значение ставки дивиденда может меняться в течение периода
действия форвардного контракта, поэтому для такого случая в
расчетах следует использовать среднюю ставку дивиденда. Значение ставки дивиденда обозначим через q.
Предположим, имеется акция, курс спот которой составляет 50
руб., через три месяца на нее выплачивается дивиденд, непрерывно начисляемая ставка которого равна 8%, ставка без риска 10%.
Необходимо определить форвардную цену, если контракт заключается на три месяца, выплата дивиденда происходит до поставки
акции по контракту. Как и в предыдущих примерах, инвестор
имеет две альтернативы. I. Купить акцию сегодня и получить на
нее через три месяца дивиденд. II. Заключить сегодня форвардный
контракт на приобретение акции через три месяца, инвестировать
на этот период под ставку без риска дисконтированную стоимость
форвардной цены и дисконтированную стоимость суммы, эквивалентную величине дивиденда, выплачиваемого на акции. Согласно первой стратегии в начале трехмесячного периода
инвестируется 50 руб. В соответствии со второй стратегией инвестируется сумма, равная:
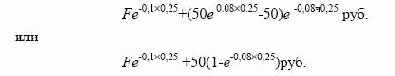
Суммы, инвестируемые в обоих случаях, должны быть равны,
иначе возникнет возможность совершить арбитражную операцию,
Поэтому
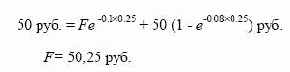
Таким образом, если форвардная цена будет больше 50,25 руб.,
то инвестор продаст контракт и купит акцию. Если форвардная
цена меньше 50,25 руб., то инвестор продаст акцию и купит контракт. Запишем наши рассуждения в общей форме и выведем формулу для определения форвардной цены. В соответствии с первой
стратегией вкладчик инвестирует цену спот акции, то есть S. Согласно второй стратегии инвестируется величина
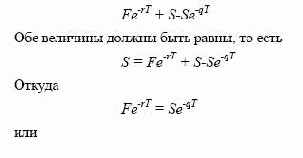
Предположим теперь, что через некоторое время после его заключения контракт продается на вторичном рынке. Поскольку на
рынке возникла уже новая форвардная цена, то для реализации
второй стратегии инвестор должен заплатить за контракт некоторую сумму f. В итоге должно соблюдаться равенство:
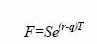
где t — время от момента покупки до истечения контракта. Отсюда
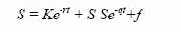
Как мы определили, форвардная цена для момента t равна:
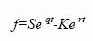
Подставив значение S из формулы (11) в формулу (10), получаем
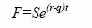
Вернемся теперь к нашему примеру и определим стоимость
форвардного контракта, если он продается за два месяца до его
истечения, и цена спот акции в этот момент равна 52 руб. В соответствии с формулой получаем:
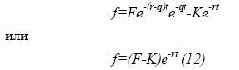
Приведем теперь более строгое доказательство определения
форвардной цены и цены форвардного контракта. Предположим,
имеется два портфеля. В портфель А входит длинный форвардный
контракт на акцию, непрерывно начисляемая ставка дивиденда
которой равна q, и сумма дисконтированной стоимости цены по-
ставки Ке-rT . В портфель Б входит акция на сумму Se-qT .
По завершении периода T портфель А будет состоять из одной
акции, так как сумма К используется для ее приобретения по
форвардному контракту. Портфель Б также состоит из одной акции, поскольку
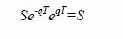

г) Форвардная цена и цена форвардного контракта на валюту
Форвардный контракт на валюту можно рассматривать как
контракт на акцию, для которой известна ставка непрерывно начисляемою дивиденда. В качестве данной ставки принимается
ставка без риска, которая существует в стране этой валюты, поскольку вкладчик может получить на нее доход, инвестировав свои
средства под процент без риска. Поэтому для определения форвардной цены мы можем воспользоваться формулой (9), скорректировав ее следующим образом:
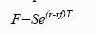
где S — цена спот единицы иностранной валюты (валюта, которую покупают), выраженная в национальной валюте (валюта, которую продают);
r — непрерывно начисляемая ставка без риска для национальной валюты;
rf — непрерывно начисляемая ставка без риска для иностранной валюты.
Цена форвардного контракта соответственно равна:
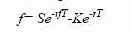
Приведенные формулы можно доказать следующим образом.
Инвестор имеет две альтернативы. I. Купить иностранную валюту
на сумму S национальной валюты сегодня. В этом случае в течение
последующего периода T он имеет возможность получить на нее
процент, равны rf. II. Купить форвардный контракт на приобретение иностранной валюты в будущем. Чтобы располагать к концу
периода T точно таким же финансовым результатом, как и в первом
случае, ему сегодня необходимо инвестировать приведенную стоимость форвардной цены и приведенную стоимость той суммы
процентов, которая будет эквивалентна доходу на иностранную
валюту по первой стратегии, то есть
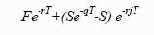
Поэтому средства, которые инвестируются в первом и втором
случаях в начале периода Г, должны быть равны, то есть
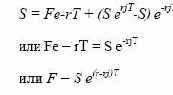
Если форвардный контракт покупается на вторичном рынке, то
в правую часть уравнения (18) необходимо подставить стоимость
форвардного контракта f В итоге получаем:
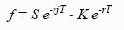
Приведем более строгое доказательство для предложенных формул. Допустим, имеется два портфеля. В портфель А входит один
длинный форвардный контракт на приобретение единицы иностранной валюты и сумма денег, равная приведенной стоимости
цены поставки Ке-rT . Портфель Б содержит дисконтированную
стоимость единицы иностранной валюты Se-rfT.
По завершении периода T портфель А состоит из единицы иностранной валюты, поскольку сумма K национальной валюты была
обменена на единицу иностранной валюты. Портфель Б также
состоит из единицы иностранной валюты. Поскольку стоимость
портфелей равна в конце периода Г, то она равна и в начале этого
периода, то есть
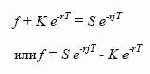
В момент заключения контракта его стоимость равна нулю, а
форвардная цена равна цене поставки, поэтому
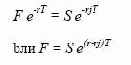
Если ставка без риска для иностранной валюты будет больше
ставки без риска для национальной валюты, то для более отдаленных периодов времени форвардная цена будет понижаться, если
же r > rf, то форвардная цена будет возрастать.
Содержание раздела