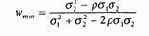|
Доля средств, вложенная в рискованный актив 1 (%) |
Доля средств, вложенная в рискованный актив 2 (%) |
Ожидаемая ставка доходности |
Стандартное отклонение |
|
0 |
100 |
0,0800 |
0,1500 |
|
25 |
75 |
0,0950 |
0,1231 |
|
36 |
64 |
0,1016 |
0,1200 |
|
50 |
50 |
0,1100 |
0,1250 |
|
100 |
0 |
0,1400 |
0,2000 |
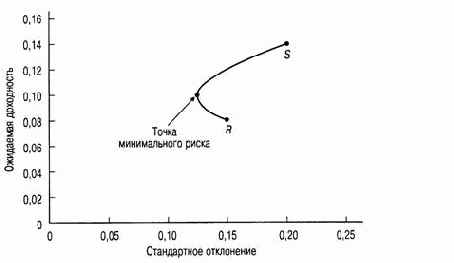
Рис. 12.3. Кривая соотношения риск/доходность: только рискованные активы
Давайте с помощью табл. 12.3 исследуем кривую, соединяющую на рис. 12.3 точки R и S. Начнем с точки R и переместим часть наших капиталов из рискованного актива 2 в рискованный актив 1. При этом наблюдается не только повышение средней ставки доходности, но и снижение стандартного отклонения. Оно снижается до тех пор, пока мы не получим портфель, который на 36% состоит из инвестиций в рискованный актив 1 и на 64% — в рискованный актив 26.
Эта точка характеризует портфель с минимальной дисперсией (minimum-variance portfolio), состоящий из рискованного актива 1 и рискованного актива 2. Если в рискованный актив 1 инвестируется более 36% общего капитала, то стандартное отклонение портфеля увеличивается.
Контрольный вопрос
Каково среднее значение доходности и ее стандартное отклонение для портфеля, который на 60% состоит из рискованного актива 1 и на 40% — из рискованного актива 2, если их коэффициент корреляции равен 0,1
Формула, описывающая долю рискованного актива 1, которая минимизирует дисперсию портфеля, выглядит следующим образом: