Мы уже говорили о том, что в основе импульсивных гармонических моделей должен лежать сетап с базовой конструкцией Z. Именно этот факт является определяющим в процессе идентификации и обозначения гармонических волновых конфигураций. Однако, ввиду наличия существенного субъективизма при волновой разметке, в процессе выделения гармонических конструкций иной раз бывает достаточно сложно однозначно сказать, что это за модель представлена на графиках.
Обычно, это присуще очень сложным гармоническим моделям, поэтому, в этих случаях приходится считать количество волн, и уже потом, по матрице, определять тип формации. Но об этом чуть позже. Итак, как показано в предыдущей таблице, количество волн в моделях второго порядка должно всегда соответствовать одному из чисел представленного ниже ряда. Берем формулу, и по ней вычисляем.
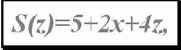
где: x - Количество трех волновых вложений,
z - Количество пяти волновых вложений.
Если в качестве примера рассмотреть правильную гармоническую волновую формацию xZ(z)x, то согласно данной формуле получим:
S(z)=5+2*2+4*1=13 волн.
Как упражнение по закреплению пройденного материала, попробуйте самостоятельно нарисовать эту гармоническую формацию, и убедитесь в правильности наших расчетов.
Далее обратим внимание на таблицу импульсивных гармонических структур, приведенную ниже. Легко заметить, что в ней указаны только правильные модели, а именно, модели с симметричной волновой структурой и пропорциональными размерами. Появление этих образований на графиках цен являет собой пример классического анализа гармонических моделей. Минусом представленной таблицы является то, что, во-первых, она не охватывает неправильные конструкции, а во-вторых, не учитывает фундаментальные закономерности, заложенные в основе строения сетапов импульсивных гармонических моделей, и это, самое главное. Единственное, что она отражает - это взаимосвязь между количеством волн и типом гармонической модели.
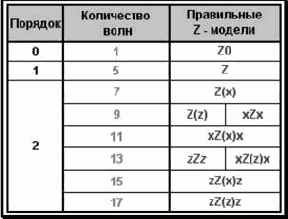
Таблица 3 Перечень правильных Z-моделей
В связи с этим, я решил перестроить таблицу таким образом, чтобы с первого взгляда можно было увидеть самые важные закономерности, заложенные в импульсивных гармонических моделях. Учитывая изложенную выше информацию, получилась такая таблица, которую я назвал «матрица импульсивных структур». Давайте проанализируем матрицу, где представлено распределение Z моделей, а так же приведено суммарное количество волн по каждой из формаций (вверху справа).
Для этого отмечу, что красными символами на самой верхней строке матрицы указаны разновидности «внутренних» вложений – ноль (или пусто), х, z. То же самое, расположено в первом столбце матрицы, но уже обозначает внешние вложения.
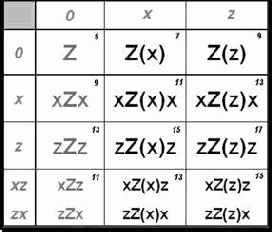
Таблица 4 Матрица импульсивных структур
Таким образом, хорошо видно, каким именно образом формируются гармонические волновые модели. В основе любой конструкции второго порядка, всегда должна лежит более простая модель, которую мы называем сетап или ядро. Для Z-моделей, такими сетапами будут являться формации типа Z, Z(x) и Z(z). Все они расположены во второй сверху строке матрицы. Заканчивая рассматривать сетапы, перейдем к более сложным гармоническим структурам. Они сформированы посредством добавления внешних вложений. Как уже говорилось, в левом крайнем столбце, красным цветом, выделены разновидности этих вложений.
Добавление их к ядру конструкции (с использованием принципа симметрии), приводит к образованию совершенно новых, и абсолютно разных гармонических волновых моделей. Обратите внимание, что все эти модели, за исключением последней строки матрицы, будут иметь правильную, симметричную структуру. Теперь вы видите, каким образом получаются модели типа – zZ(x)z или xZ(z)x и т.д.
Кстати, интересным так же представляется тот, факт, что пяти волновая, базовая конструкция Z, с точки зрения «матрицы импульсивных структур», является ничем иным, как обычным Z - сетапом с нулевыми (пустыми) вложениями в начале, середине и конце конструкции. И это действительно так! Как выясняется, матричное представление импульсивных гармонических моделей, гораздо лучше и доступней объясняет многие, казалось бы, непонятные вещи, связанные с формированием гармонических структур. Поэтому, изучение гармонических моделей, мы начнем с рассмотрения важной составляющей любой сложной конструкции – сетапа или ядра гармонической конструкции.
